Veta demonštrácie existencie a jedinečnosti, príklady a cvičenia

On Veta existencie a jedinečnosti Stanovuje potrebné a dostatočné podmienky pre diferenciálnu rovnicu prvého poradia s daným počiatočným stavom, aby mali riešenie a že toto riešenie je tiež jediné. 

Veta však nedáva žiadnu techniku ​​ani indikáciu toho, ako nájsť takéto riešenie. Veta existencie a jedinečnosti sa tiež rozširuje na diferenciálne rovnice vyššieho poriadku s počiatočnými podmienkami, ktoré sú známe ako problém Cauchy.

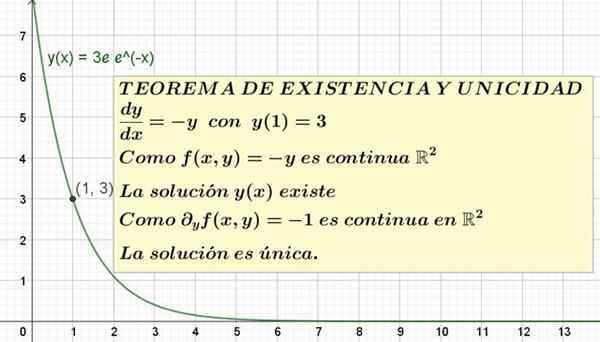
postava 1. Diferenčná rovnica s počiatočným stavom a jej roztok je zobrazená. Veta existencie a jedinečnosti zaručuje, že je jediným možným riešením.

Formálne vyhlásenie o vete existencie a jedinečnosti je nasledujúce:

„Pre diferenciálnu rovnicu a '(x) = f (x, y) s počiatočným stavom a (a) = b,  existuje Aspoň jedno roztok v obdĺžnikovej oblasti roviny Xy obsahujúci bod (A, b), Jo f (x, y) V tomto regióne je nepretržitý. A ak čiastočný derivát F mať rešpekt z a: G = ∂f/ ∂y Je nepretržitý v tej istej pravouhlej oblasti, takže riešenie je jedinečné v prostredí bodu (A, b) obsah v oblasti kontinuity F a g.„

Užitočnosť tejto vety leží najskôr, aby vedela, aké sú oblasti XY roviny, v ktorej môže existovať riešenie a tiež vedieť, či je nájdené riešenie jediné, alebo či sú iní. 

Všimnite si, že v prípade, že stav jedinečnej.

[TOC]

Demonštrácia vety existencie a jedinečnosti

Obrázok 2. Charlesovi Emile Picardovi (1856-1941) je akreditovaná jedna z prvých demonštrácií existencie a jedinečnosti. Zdroj: Wikimedia Commons.

Pre túto vetu sú známe dve možné demonštrácie, jednou z nich je demonštrácia Charlesa Emile Picarda (1856-1941) a druhá je spôsobená Giuseppe Peano (1858-1932) na základe diel Augustina Louisa Cauchyho (1789-1857 ).

Môže vám slúžiť: Súbežné vektory: Charakteristiky, príklady a cvičenia

Je potrebné poznamenať, že najjasnejšie matematické mysle devätnásteho storočia sa zúčastnili na demonštrácii tejto vety, takže môže byť intuit, že ani jedna z nich nie je jednoduchá.

Na formálne demonštrovanie vety je potrebné najprv vytvoriť sériu pokročilejších matematických konceptov, ako sú funkcie typu Lipschitz, Banachové priestory, karatheodory a niekoľko ďalších existenčných vety, ktoré unikajú účelu článku.

Veľká časť diferenciálnych rovníc, s ktorými sa zaobchádza s fyzikou, sa zaoberajú súvislými funkciami v záujmových regiónoch, preto sa obmedzíme na preukázanie spôsobu, akým sa veta aplikuje v jednoduchých rovniciach.

Príklady

- Príklad 1

Zvážte nasledujúcu diferenciálnu rovnicu s počiatočnou podmienkou:

a '(x) = - y; s a (1) = 3

Existuje riešenie pre tento problém? Je to jediné možné riešenie?

Odpovedať

Po prvé, vyhodnocuje sa existencia riešenia diferenciálnej rovnice a že spĺňa aj pôvodnú podmienku. 

V tomto príklade f (x, y) = - y Podmienka existencie si vyžaduje vedieť, či  f (x, y) Je nepretržitý v oblasti lietadla Xy obsahujúci súradnicový bod x = 1, y = 3.

ale f (x, y) = -y Je to príbuzná funkcia, ktorý je nepretržitý v oblasti reálnych čísel a existuje v celom rozsahu skutočných čísel.

Preto sa dospelo k záveru, že f (x, y) je v R kontinuálny², Takže veta zaručuje existenciu aspoň jedného riešenia.

Keď to viete, je čas posúdiť, či je riešenie jedinečné alebo naopak, je viac ako jedna. Z tohto dôvodu je potrebné vypočítať čiastočný derivát F Pokiaľ ide o premennú a:

∂f/∂y = ∂ (-y)/∂y = -1

Tak G (x, y) = -1 čo je konštantná funkcia, ktorá je tiež definovaná pre všetky r² A je tam tiež nepretržitý. Z toho vyplýva, že veta existencie a jedinečnosti zaručuje, že tento problém s počiatočnou hodnotou má jedinečné riešenie, hoci nám to nehovorí, čo to je.

Môže vám slúžiť: konvexný polygón: definícia, prvky, vlastnosti, príklady

- Príklad 2

Zvážte nasledujúce prvé -rdérne bežné diferenciálne rovnice s počiatočnou podmienkou:

a '(x) = 2√y; a (0) = 0.

Existuje riešenie a (x) Pre tento problém? Ak áno, určte, či existuje jeden alebo viac ako jeden.

Odpoveď

Považujeme funkciu f (x, y) = 2√y. Funkcia F je definovaný iba pre y≥0, Vieme, že negatívne číslo nemá skutočný koreň. Okrem f (x, y) Je nepretržitý v hornom semiféne R²  vrátane osi x, tak Veta existencie a jedinečnosti zaručuje Aspoň jedno riešenie v tejto oblasti.

Teraz je počiatočná podmienka x = 0, y = 0 na okraji oblasti roztoku. Potom vezmeme čiastočný derivát F (x, y) vzhľadom na y:

∂f/∂y = 1/√y

V tomto prípade funkcia nie je definovaná pre y = 0, presne tam, kde je počiatočná podmienka.

Čo nám hovorí vetu? Hovorí nám, že hoci vieme, že existuje aspoň jedno riešenie, horný semifiel osi x vrátane osi X, pretože stav jedinečnosti nie je splnený, neexistuje žiadna záruka, že existuje jediné riešenie.

To znamená, že v oblasti kontinuity F (x, y) by mohlo byť jedno alebo viac roztoku). A ako vždy, veta nám nehovorí, čo by mohlo byť.

Vyriešené cvičenia

- Cvičenie 1

Vyriešte problém s Cauchy v príklade 1:

a '(x) = - y; s a (1) = 3. 

Nájdite funkciu y (x), ktorá spĺňa diferenciálnu rovnicu a počiatočnú podmienku.

Riešenie

V príklade 1 sa zistilo, že tento problém má riešenie a je tiež jedinečný. Ak chcete nájsť riešenie, prvá vec, ktorú by sa malo všimnúť, je to, že ide o prvú diferenciálnu rovnicu oddeľovateľných premenných, ktorá je napísaná takto:

Môže vám slúžiť: Variačný koeficient: pre čo ide, výpočet, príklady, cvičenia

dy /dx = - a → dy = -y dx

Rozdelenie medzi oboma členov a v oboch členoch, aby sme oddelili premenné, ktoré máme:

dy/y = - dx

Uplatňuje sa neurčitý integrál v oboch členoch:

∫ (1/y) dy = - ∫dx

Riešenie neurčitých integrálov je:

ln (y) = -x + c

kde C je konštanta integrácie, ktorá je určená počiatočnou podmienkou:

ln (3) = -1 + c, to znamená, že c = 1 + ln (3)

Výmena hodnoty C a reorganizácie je:

ln (y) - ln (3) = -x + 1

Uplatňovanie nasledujúcej vlastnosti logaritmov:

Rozdiel v logaritmoch je kvocient logaritmus

Predchádzajúci výraz možno prepísať takto:

ln (y/3) = 1 - x

Exponenciálna funkcia sa uplatňuje u oboch členov na získanie:

Y / 3 = e^{(1 - x)}

Čo je rovnocenné:

 y = 3e e^-X

Toto je jedinečné riešenie rovnice a '= -y s y (1) = 3. Graf tohto roztoku je znázornený na obrázku 1.

- Cvičenie 2

Nájdite dve riešenia problému nastoleného v príklade 2:

a '(x) = 2√ (y); a (0) = 0.

Riešenie

Je to tiež rovnica samostatných premenných, ktoré sú napísané odlišne, zostáva:

D Y / √ (y) = 2 dx

Ak vezmeme neurčitú integrál v oboch členoch: zostáva:

2 √ (y) = 2 x + c

Ako je známe y≥0 V oblasti roztoku máme:

y = (x + c)² 

Ale ako počiatočná podmienka x = 0, musí byť splnená y = 0, potom konštanta C je nula a nasledujúce riešenie zostáva:

a (x) = x².

Ale toto riešenie nie je jedinečné, funkcia y (x) = 0 je tiež riešením nasadeného problému. TEOREM existencia a jedinečnosť použitá na tento problém v príklade 2 už predpovedala, že môže existovať viac ako jedno riešenie.

Odkazy

1. Coddington, gróf a.; Levinson, Norman (1955), Teória bežných diferenciálnych rovníc, New York: McGraw-Hill.
2. Encyklopédia matematiky. Cauchy-Lipschitzova veta. Získané z: Encyclopediaofmath.orgán
3. Lindelöf, South L'A Aplikácia Metode des A Aprocations následky Aux équations Différentielles Ordinaires du Premier Ordre; Compttes rendus hebdomadaires des séances de l'Anc acadequie des sciences. Zvuk. 116, 1894, s. 454-457. Získané z: Gallic.Bnf.fr.
4. Wikipedia. Picardova následná metóda prístupu. Obnovené z: je.Wikipedia.com
5. Wikipedia. Veta picard-lindelöf. Obnovené z: je.Wikipedia.com.
6. Zill, D.1986. Základné diferenciálne rovnice s aplikáciami.Sála.