Vysvetlenie Faktorová veta, príklady, cvičenia

On faktorová veta uvádza, že polynóm P (x) je deliteľný binomiálnym formám (x - a), ak x = a je koreň p (x), to je p (a) = 0. Hovorí sa, že polynóm je deliteľný medzi iným, keď je jeho zvyšok alebo odpočinok nula.

Polynóm je vyjadrením formy:

P (x) = a_n Xⁿ + do_N-1 X^N-1 +… + A₁ x + a₀

postava 1. Faktorová veta. Zdroj: f. Zapata.

Kde:

-n je stupeň polynómu, ktorý je najväčším celočíselným číslom, na ktorý nezávislá premenná x stúpa,

-Cení a_n, do_N-1 ,… + A₁ , do₀ Sú to koeficienty polynómu, ktoré sú vo všeobecnosti skutočné čísla, ale môžu to byť aj zložité čísla.

Polynóm triedy N sa môže rozkladať ako produkt binomiálov formy:

(X - r_Jo)

Kde r_Jo Je to koreň i-alkish p (x):

P (x) = a_n (X - r₁) (X - r₂)… (X - r_n)

Pretože počet koreňov polynómu sa rovná rovnakému stupňu.

[TOC]

Príklady

- Príklad 1

Zvážte polynóm v prípade:

P (x) = 3⋅x² - 7 hlúz + 2

Chcete vedieť, či je tento polynóm deliteľný Binomial (x - 2). Ak sa používa veta faktorov, musíme vyhodnotiť p (x = 2), aby sme vedeli, či hodnota 2 je koreň alebo nie je. Potom pokračujeme v vyhodnotení výrazu:

P (2) = 3 štvory 222 - 7 štrí 2 = 3,4 - 7 hlúpy 2 = 12 - 14 + 2 = 12 - 12 = 0.

Ukazuje sa, že x = 2 je koreň p (x), takže podľa vety faktorov je binomiálny (x - 2) skutočne faktorom p (x).

Prejdime na priame overenie divízie. Podrobnosti o tom, ako sa delenie vytvára, je uvedený na nasledujúcom obrázku:

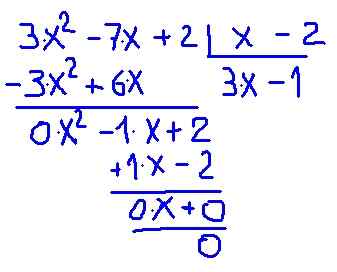Obrázok 2.- Polynomiálne divízia P (x) medzi binomickým X-2. Zdroj: f. Zapata.

Je overené, že kvocient medzi p (x) a (x -2) poskytuje polynóm menšieho stupňa nazývaný kvocient c (x) = 3⋅x - 1 so zvyškom 0.

Môže vám slúžiť: vektorové funkcie

Výsledok môžeme zhrnúť takto:

(3⋅x² - 7⋅x + 2) ÷ (x -2) = (3 Dobre - 1) + 0

Predchádzajúci výraz je možné napísať iným spôsobom, jednoducho nezabudnite, že dividenda P (x) sa rovná produktu deliteľa (x -2) kvocientom (3 Dobre - 1) plus zvyšok (v tomto prípade nula nula (nula v tomto prípade nula. ):

(3⋅x² - 7⋅x + 2) = (x -2) (3⋅x - 1) + 0

Týmto spôsobom p (x) polynóm (x), to znamená, napíšte ako produkt polynómov, pôvodný polynóm: pôvodný polynóm:

(3⋅x² - 7⋅x + 2) = (x -2) (3⋅x - 1)

- Príklad 2

Byť polynomiálny q (x) = x³ - x + 2. Chcete vedieť, či je deliteľný binomial (x + 1).

Najpriamejším spôsobom je jednoducho uplatniť vetu faktorov. V takom prípade musíte jednoducho overiť, či x = -1 sa annuluje alebo nie polynóm q (x).

Pokračujeme nahradením:

Q (-1) = (-1)³ - (-1) + 2 = -1 + 1 + 2 = 2

Výsledok sa líši od nuly, preto veta faktorov zaisťuje, že polynóm Q (x) nie je deliteľný medzi (x + 1), pretože q (-1) ≠.

Teraz bude rozdelenie q (x) medzi binomiálnym (x + 1) vyrobenými ako metóda overovania nášho záveru.

Pri tejto príležitosti sa divízia uskutoční metódou syntetického delenia, ktorá spočíva v umiestnení v prvom ročníku v prvom ročníku, všetky koeficienty polynómu vrátane chýbajúcich, pretože majú nulový koeficient.

Potom je v prvom stĺpci umiestnený nezávislý termín deliteľa, ale so zmenou značky je v našom prípade deliteľ (x + 1). Jeho nezávislý termín je 1, ale rovnako ako v prvom stĺpci je umiestnený zmenený znak, tj -1.

Nasledujúci obrázok zobrazuje, ako sa vykonáva syntetické delenie:

Môže vám slúžiť: polynómové rovnice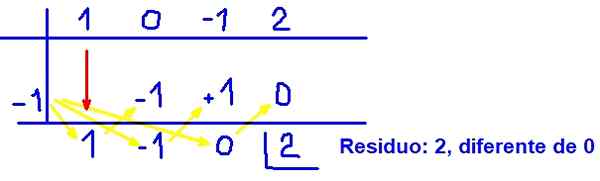Obrázok 3. Príklad polynómového syntetického delenia. Zdroj: f. Zapata.

S týmto výsledkom je dokázané, že (x + 1) to nie je faktor polynómu q (x) = x³ - x + 2 Pretože zvyšok nie je nula.

Tento záver nie je prekvapený, pretože už bol predpovedaný s faktorovou vetou. Všimnite si, že pri výmene x = -1 v Q (x), čo sa získava, je presne zvyšok alebo zvyšok polynómového delenia, pretože q (-1) = zvyšok = 2.

Divízia samozrejme poskytuje ďalšie informácie o kvociente C (x) = x² - X.

Pamätajte si, že dividenda Q (x) sa rovná deliteľovi (x + 1) podľa pomeru C (x) plus zvyšok r = 2 Máme expanziu polynómového q (x) nasledovne:

Q (x) = (x + 1) (x² - x) + 2 = x (x + 1) (x - 1) + 2

Je potrebné poznamenať, že tento výraz nie je faktorizáciou uvedeného polynómu, pretože existuje neprináškový výraz, ktorý je presne hodnotou hodnoty 2.

Cvičenia

- Cvičenie 1

Nájdite polynómové faktory

P (x) = x³ - 5 x² + 2 x + 8

A tiež napíšte svoju faktorizáciu.

Riešenie

Faktorová veta naznačuje, že musíme hľadať korene do a potom nájdite faktory (x - do), V tomto prípade, pretože je to polynóm triedy tri, musia existovať tri korene. 

Pretože ide o polynóm s celkovými koeficientmi, korene musia byť medzi deliteľmi nezávislého pojmu, ktoré v tomto prípade 8. Títo deliaci sú:

± 1, ± 2, ± 4, ± 8.

Začneme skúmaním +1: p (+1) = 1³ - 5lek 1² + 2 ÁNO 1 + 8 = 1 - 5 + 2 + 8 = 6, ktoré sa líši od 0, preto +1 nie je korene.

Preskúmame -1:

P (-1) = (-1)³ - 5lek (-1)² + 2lek (-1) + 8 = -1 - 5 - 2 + 8 = 0

Z výsledku sa dospelo k záveru, že -1 je koreň p (x) y (x -( -1)) = (x + 1) je polynomický faktor.

Môže vám slúžiť: minimálne štvorce

Potrebujeme nájsť ďalšie dva faktory:

Vyskúšali sme ďalší, ktorý je +2:

P (+2) = (+2)³ - 5lek (+2)² + 2lek (+2) + 8 = 8 + (-20) + 4 + 8 = 0

Opäť dostaneme nulu. Potom je druhým faktorom (x - 2).

Pretože je to polynóm triedy tri, potrebujeme iba nájsť faktor. Teraz sme sa pokúsili zistiť, či polynóm ruší:

P (+4) = (+4)³ - 5lek (+4)² + 2lek (+4) + 8 = 64 - 80 + 8 + 8 = 0.

Inými slovami.

Nemusíte stále hľadať, pretože je to polynóm triedy 3, ktorý má najviac tri korene. V tomto cvičení sa všetky korene ukázali ako skutočné a celé.

Preto je polynóm P (x) faktorom:

P (x) = x³ - 5 x² + 2 x + 8 = (x + 1) (x - 2) (x - 4).

- Cvičenie 2

Byť polynómom p zajtra³ - x + 2p. Stanovte hodnotu P pre polynóm, aby bol deliteľný (x + 2).

Riešenie

Používame faktorovú vetu, ktorá uvádza, že ak x = -2 zruší polynóm, potom (x -( -2)) je faktorom uvedeného polynómu.

Potom je X nahradený (-2) v pôvodnom polynóme, je zjednodušený a rovná nule:

Plek (-2)³ - (-2) + 2p = 8p + 2 + 2p = 10p + 2 = 0

Teraz sa hodnota P vymaže tak, aby sa rovnosť splnila na nulu:

P = -2 / 10 = --⅕ 

To znamená, že polynóm: 

-⅕⋅x³ - X - ⅖

Je deliteľný (x + 2) alebo čo je ekvivalentné: (x + 2) je jedným z jeho faktorov.

Odkazy

1. Baldor aurelio. Algebra. Redakčná skupina Patria.
2. Demana, w. Prekáculculo: grafické, numerické, algebraické 7. vydanie. Pearson Vzdelanie.
3. Jiménez, r. 2008. Algebra. Sála.
4. Stewart, J. 2006. Predbežné vycvičenie: matematika na výpočet. 5. Vydanie. Učenie sa.
5. Zill, D. 1984. Algebra a trigonometria. McGraw Hill.