Varignonova veta

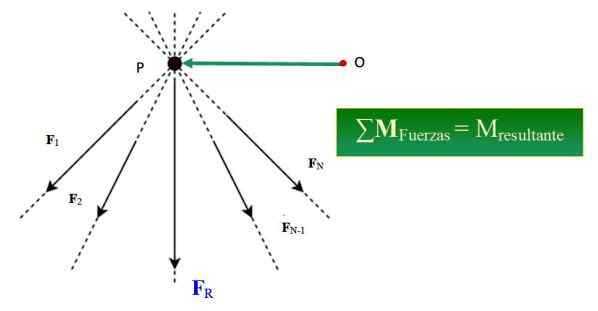
postava 1.- Varignonova veta potvrdzuje, že súčet momentu síl okolo určitého bodu je rovnocenný s časom výsledku, pokiaľ ide o tento bod. Zdroj: Wikimedia Commons/F. Zapata.

Čo je Varignonova veta?

Varigonova veta v mechanike uvádza, že súčet momentov vytvorených systémom súbežných síl vzhľadom na určitý bod sa rovná momentu výslednej sily vzhľadom na rovnaký bod.

Z tohto dôvodu je táto veta známa aj ako Začiatok okamihov.

Zatiaľ čo prvý, kto uviedol, že to bol Holanďan Simon Stevin (1548-1620), tvorca hydrostatického paradoxu, francúzsky matematik Pierre Varignon (1654-1722) bol ten, kto mu následne dal svoju definitívnu formu.

Príklad toho, ako Varigonova veta funguje v mechanike, je nasledujúci: Predpokladajme, že jednoduchý systém dvoch koplanárov a súbežných síl pôsobí na bod F₁ a F₂, (Označené tučným písmom pre jeho vektorový znak). Tieto sily vedú k sieti alebo výslednej sile, ktorá sa nazýva F_R.

Každá sila vyvíja krútiaci moment alebo moment vzhľadom na bod alebo, ktorý sa vypočíta vektorovým produktom medzi vektorom polohy r_Oproti a Strengh F, kde r_Oproti Je nasmerovaný z alebo do bodu súbežnosti P:

M_O1 = r_Oproti × F₁

M_O2 = r_Oproti × F₂

Vzhľad F_R = F₁ + F₂, tak:

M_Ani = r_Oproti × F₁ + r_Oproti × F₂ = M_O1 + M_O2

Ale ako r_Oproti Je to spoločný faktor, ktorý teda uplatňuje distribučnú vlastnosť na krížový produkt:

M_Ani = r_Oproti × (F₁ + F₂) = r_Oproti × F_R                

Preto súčet momentov alebo krútiacich momentov každej sily vzhľadom na bod alebo je rovnocenný s časom výslednej sily vzhľadom na rovnaký bod.

Vyhlásenie

Byť systémom n súbežných síl, ktoré tvorí F₁, F₂, F₃.. F_N, ktorých akcie sú určené v bode P (pozri obrázok 1), moment systému týchto síl M_Ani, Pokiaľ ide o bod alebo je daný:

Môže vám slúžiť: Nestabilná rovnováha: Koncept a príklady

M_Ani = r_Oproti × F₁ + r_Oproti × F₂ + r_Oproti × F₃ +.. r_Oproti × F_N = r_Oproti × (F₁ + F₂ + F₃ +.. F_N)

Demonštrácia

Na demonštráciu vety sa vyrába distribučná vlastnosť vektorového produktu medzi vektormi.

Byť sily F₁, F₂, F₃.. F_N aplikované na body na₁, Do₂, Do₃.._N a súbežné v bode P. Výsledný moment tohto systému, vzhľadom na bod alebo, nazývaný M_Ani, Je to súčet momentov každej sily, vzhľadom na tento bod:

M_Ani = ∑ r_Oai × F_Jo

Kde súčet prechádza z i = 1 do i = n, pretože existujú n sily. Pretože ide o súbežné sily a keďže vektorový produkt medzi paralelnými vektormi je nulová, stáva sa, že:

r_Pai × F_Jo = 0

S nulovým vektorom označeným ako 0.

Moment jednej zo síl týkajúcich sa O, napríklad sily F_Jo aplikované v a_Jo, Je to napísané takto:

M_{počul som} = r_Oai × F_Jo

Polohový vektor r_Oai  Môže sa vyjadriť ako súčet dvoch vektorových pozícií:

r_Oai = r_Oproti + r_Pai

Týmto spôsobom, okamih s ohľadom na alebo silu F_Jo je:

M_{počul som} = (r_Oproti + r_Pai) × F_Jo = (r_Oproti × F_Jo) + (r_Pai × F_Jo)

Ale posledný termín je null, ako je vysvetlené vyššie, pretože r_Pai je na línii konania F_Jo, preto:

M_{počul som} = r_Oproti × F_Jo

Vedieť, že okamih systému vzhľadom na bod alebo je súčet všetkých jednotlivých momentov každej sily vzhľadom na tento bod, potom:

M_Ani = ∑ M_{počul som} = ∑ r_Oproti × F_Jo

Ako r_Oproti Je konštantná zo súčtu:

M_Ani = r_Oproti × (∑ F_Jo)

Ale ∑ F_Jo Je to jednoducho výsledná sieť alebo sila F_R, Preto sa okamžite dospelo k záveru, že:

Môže vám slúžiť: Leyden fľaša: časti, prevádzka, experimenty

M_Ani = r_Oproti × F_R

Príklad

Varigonova veta uľahčuje výpočet momentu sily F Pokiaľ ide o bod alebo štruktúru zobrazenú na obrázku, ak je sila rozdelená na jeho obdĺžnikové komponenty a vypočíta sa moment každého z nich:

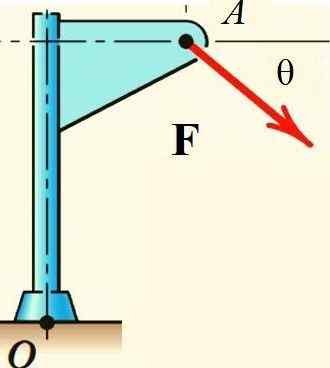Obrázok 2.- Varigonova veta sa vzťahuje na výpočet momentu sily okolo alebo. Zdroj: f. Zapata.

Aplikácie Varignonovej vety

Ak je známa sila vyplývajúca zo systému, Varignonova veta sa dá použiť na nahradenie súčtu každého momentu vytvorených silami, ktoré ho tvoria v čase výsledku.

Ak systém pozostáva z síl v tej istej rovine a bod, v ktorom chcete vypočítať moment patrí do tejto roviny, výsledný moment je kolmý.

Napríklad, ak sú všetky sily v rovine XY, moment je nasmerovaný na os Z a zostáva iba na nájdenie jeho veľkosti a jej významu, ako je prípad vyššie opísaného príkladu.

V takom prípade Varigonova veta umožňuje vypočítať moment vyplývajúci zo systému pomocou súčtu. Je to veľmi užitočné v prípade systému trojrozmerných síl, pre ktoré a priori nie je známy smer výsledného momentu.

Na vyriešenie týchto cvičení je to vhodné.

Cvičenie

Varignonovou vetou vypočítajte moment sily F okolo bodu alebo je znázornené na obrázku, či je veľkosť f 725 n.

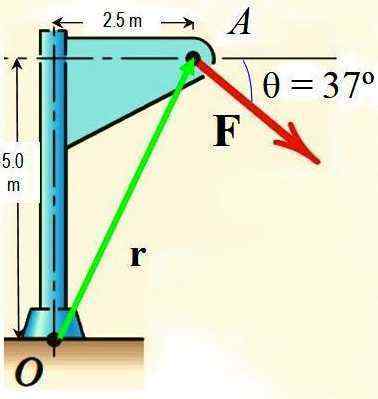Obrázok 3.- Obrázok pre cvičenie vyriešené. Zdroj: f. Zapata.

Riešenie

Ak chcete uplatniť Varigonovu vetu, sila sa rozkladá F V dvoch komponentoch, ktorých príslušné momenty okolo alebo sa vypočítavajú a pridávajú sa, aby sa dosiahol výsledný moment.

Môže vám slúžiť: pevné telo

F_X = 725 n ∙ cos 37 ° = 579.0 n

F_a = - 725 n n ∙ sen 37 ° = −436.3 n

Podobne aj vektor polohy r nasmerované z alebo na A má komponenty:

r_X = 2.5 m

r_a = 5.0 m

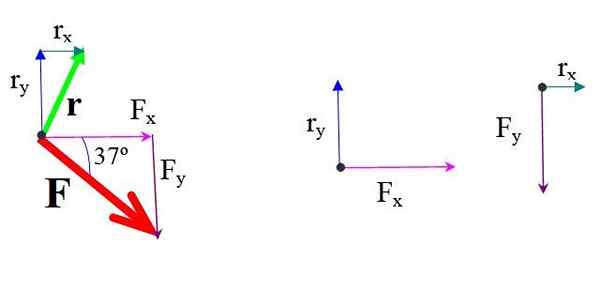Obrázok 4.- Komponenty sily a polohy. Zdroj: f. Zapata.

Moment každej zložky sily vzhľadom na alebo vynásobí silu a kolmá vzdialenosť.

Obe sily majú tendenciu striedať štruktúru rovnakým smerom, čo je v tomto prípade zmysel skóre, čo je svojvoľne priradené kladné znamenie:

M_Vôl = F_X∙ r_a ∙ Sin 90 ° = 579.0 n ∙ 5.0 m = 2895 n ∙ m

M_Odvoz = F_a∙ r_X ∙ Sin (-90 °) = −436.3 n ∙ 2.5 m ∙ (−1) = 1090.8 n ∙ m

Výsledný moment vzhľadom na alebo je:

M_Ani = M_Vôl + M_Odvoz = 3985.8 n ∙ M kolmé na rovinu a v krútiacom momente.

Odkazy

1. Bedford, 2000. Do. Mechanika pre inžinierstvo: statické. Addison Wesley. 
2. Pivo, f. 2010. Statický. McGraw Hill. 9NA. Vydanie.
3. Hibbeler, R. 1992. Mechanika pre inžinierov. 6. Vydanie. Cecsa.
4. HK inžinierstvo. Varignonova veta. Obnovené z: YouTube.com.
5. Wikipedia. Varignonova veta (Mechanics). Zdroj: In.Wikipedia.orgán.