Vysvetlenie teórie prekrytia, aplikácie, cvičenia vyriešené

On Veta superpozície, V elektrických obvodoch sa uvádza, že napätie medzi dvoma bodmi alebo prúdom cez nich je algebraický súčet napätia (alebo prúdov, ak je tomu tak), z dôvodu každého zdroja, akoby každý z nich pôsobil v a nezávislý.

Táto veta umožňuje analýzu lineárnych obvodov obsahujúcich viac ako jeden nezávislý zdroj, pretože je potrebné iba vypočítať príspevok každého z nich osobitne.

Lineárna závislosť je rozhodujúca, že sa veta uplatňuje. Lineárny obvod je ten, ktorého odpoveď je priamo úmerná vstupu.

Napríklad Ohmov zákon uplatňovaný na elektrický odpor ustanovuje, že to stanovuje V = i.R, kde Vložka Je to napätie, R je odpor a Jo Je to aktuálny. Je to potom lineárna závislosť od napätia a prúdu v odporu.

V lineárnych obvodoch sa zásada superpozície uplatňuje, berúc do úvahy nasledujúce:

-Každý nezávislý zdroj napätia sa musí posudzovať osobitne, a preto je potrebné vypnúť všetky ostatné. Stačí dať 0 V všetky tie, ktoré nie sú podrobené analýze alebo ich nahradia v schéme skratom.

-Ak je zdroj, musí sa obvod otvoriť.

-Ak sa berie do úvahy vnútorný odpor prúdu aj zdrojov napätia, musia zostať na svojom mieste a sú súčasťou zvyšku obvodu.

-Ak existujú závislé zdroje, musia byť tak, ako sa objavujú v obvode.

[TOC]

Žiadosti

Prekrývajúca veta sa používa na získanie jednoduchších a ľahších obvodov na zvládnutie obvodov. Je však potrebné mať na pamäti, že sa vzťahuje iba na osoby s lineárnymi reakciami, ako je uvedené na začiatku.

Potom sa nemôže použiť priamo na výpočet napájania, pretože výkon súvisí so prúdom cez:

P = i² R

Pretože prúd je na druhú, odpoveď nie je lineárna. Nie je použiteľné ani na magnetické obvody, v ktorých zasahujú transformátory.

Môže vám slúžiť: dynamická elektrina

Na druhej strane, veta superpozície poskytuje príležitosť poznať účinok, ktorý má každý zdroj na obvod. A samozrejme, prostredníctvom svojej aplikácie je možné ho úplne vyriešiť, to znamená poznať prúdy a napätie prostredníctvom každého odporu.

Prekrývajúca sa veta sa dá použiť aj v spojení s inými vetami obvodu, napríklad teorémmi Thévenina, na vyriešenie zložitejších konfigurácií.

V obvodoch striedavého prúdu je tiež užitočná veta. V tomto prípade pracujeme s impedanciami namiesto odporov, pokiaľ je možné vypočítať celkovú odozvu každej frekvencie nezávislých.

Nakoniec, v elektronických systémoch je veta použiteľná pre priamu aj alternatívnu analýzu prúdu osobitne.

Kroky na použitie vety prekrývania

-Deaktivujte všetky nezávislé zdroje podľa pokynov uvedených na začiatku, s výnimkou toho, čo sa má analyzovať.

-Stanovte výstup, buď napätie alebo prúd, ktorý vytvára tento jediný zdroj.

-Opakujte dva kroky opísané pre všetky ostatné zdroje.

-Vypočítajte algebraický súčet všetkých príspevkov zistených v predchádzajúcich krokoch.

Vyriešené cvičenia

Príklady vyriešené nižšie objasňujú použitie vety v niektorých jednoduchých obvodoch.

- Príklad 1

V obvode znázornenom na nasledujúcom obrázku nájdite prúd, ktorý prechádza každým odporom cez prekrývajúcu vetu.

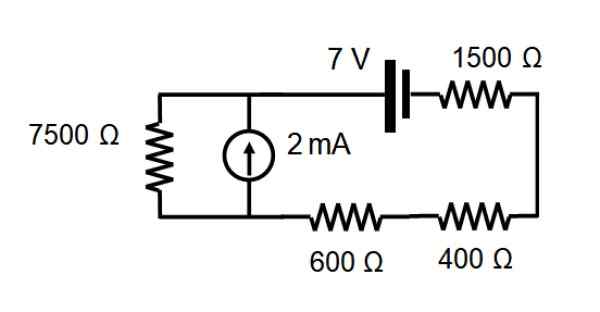
Riešenie

Príspevok zdroja napätia

Na spustenie aktuálneho zdroja je eliminovaný, s ktorým obvod zostáva týmto spôsobom:

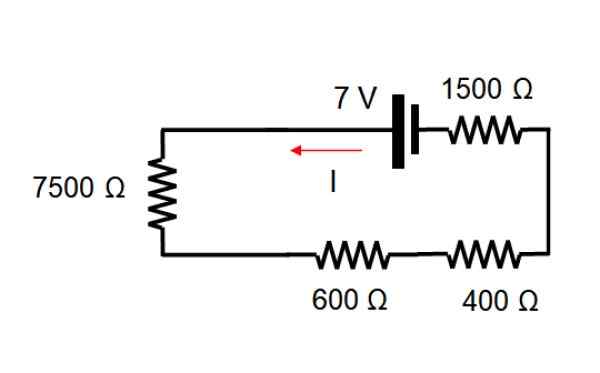
Ekvivalentný odpor pridáva hodnotu každého odporu, pretože sú všetky v sérii:

7500 +600 +400 +1500 Ω = 10.000 Ω

Uplatňovanie Ohmovho zákona V = i.R A zúčtovanie prúdu:

I = v / r = 7/10.000 a = 0.0007 a = 0.7 mA

Tento prúd je rovnaký pre všetok odpor.

Môže vám slúžiť: Millikan Experiment: Postup, vysvetlenie, dôležitosť

Príspevok súčasného zdroja

Zdroj napätia je okamžite eliminovaný, funguje iba so súčasným zdrojom. Výsledný obvod je uvedený nižšie:

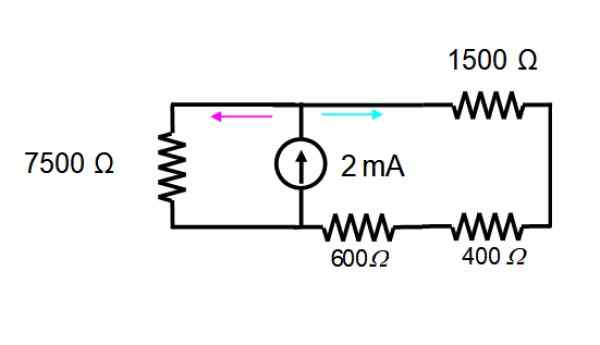
Odpory v sieťach napravo sú v sérii a môžu byť nahradené iba jedným:

600 +400 + 1500 Ω = 2500 Ω

Výsledný obvod je taký:

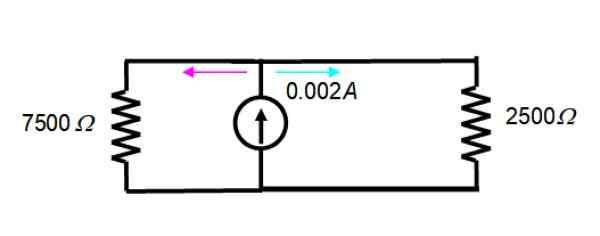
Prúd 2 mA = 0.002 A je rozdelená medzi dva odpory obrázku, preto je rovnica súčasného deliteľa platná:

Jo_X = (R_rovnica/R_X)_Tón

Kde Jo_X je prúd v odporu R_X, R_rovnica symbolizuje rovnocenný odpor a Jo_Tón je celkový prúd. Je potrebné nájsť medzi nimi rovnocenný odpor s nimi, pretože vie:

1/r_rovnica = (1/ r₁) + (1/ r₂)

Preto:

1/r_rovnica = (1/7500) + (1/2500) = 1/1875 → R_rovnica = 1875 Ω

Pre tento ďalší obvod prúd, ktorý prechádza odporom 7500 Ω, nahradí hodnoty v prúdovej deliacej rovnici:

Jo_{7500 Ω} = (1875/7500). 0.002 A = 0.0005 a = 0.5 mA

Zatiaľ čo ten, ktorý prechádza odporom 2500 Ω, je:

Jo_{2500 Ω} = 2 mA - 0.5 mA = 1.5 mA

Aplikácia superpozície

Teraz sa používa prekrývajúca veta pre každý odpor, počnúc 400 Ω:

Jo_{400 Ω} = 1.5 mA - 0.7 mA = 0.8 mA

Dôležitý: Pre tento odpor sa prúdy odpočítajú, pretože cirkulujú v opačnom smere, ako je zrejmé od starostlivého pozorovania obrázkov, v ktorých majú zmysly prúdov rôzne farby.

Rovnaký prúd ide rovnako k odporu 1500 Ω a 600 Ω, pretože sú všetky v sérii.

Potom sa veta aplikuje na nájdenie prúdu prostredníctvom odporu 7500 Ω:

Jo_{7500 Ω} = 0.7 mA + 0.5 mA = 1.2 mA

Dôležitý: V prípade odporu 7500 Ω pozorujte, že prúdy sa pridávajú, pretože v obidvoch obvodoch cirkulujú rovnakým smerom pri prechádzaní týmto odporom. Opäť je potrebné pozorne pozorovať zmysly prúdov.

Môže vám slúžiť: relatívna chyba: vzorce, ako sa vypočítajú, cvičenia

- Cvičenie 2

Nájdite prúd a napätie prostredníctvom odporu 12 Ω cez prekrývajúcu vetu.

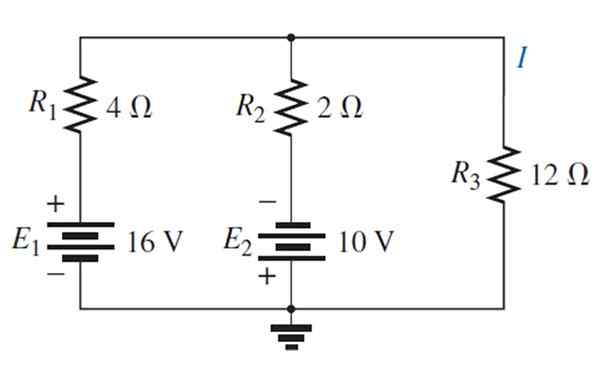
Riešenie

Zdroj E je vymenený₁ So skratom:

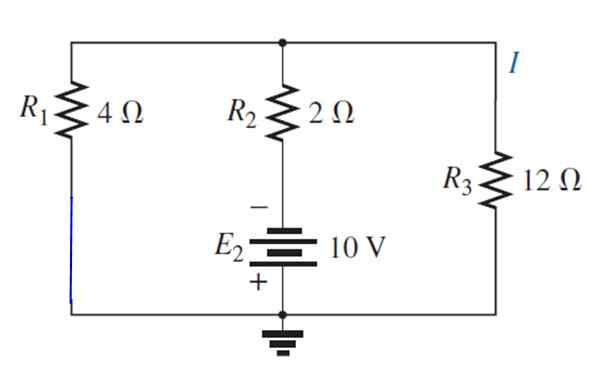
Výsledný obvod je nakreslený nasledovne, aby sa ľahko vizualizovali odpor, ktoré zostávajú paralelne:

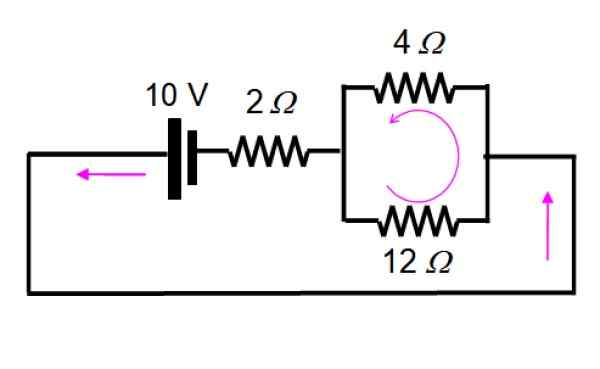
A teraz je vyriešená použitím sérií a paralelných:

1/r_rovnica = (1/12) + (1/4) = 1/3 → r_rovnica = 3 Ω

Tento odpor je zase v sérii s odporom 2 Ω, Preto je celkový odpor 5 Ω. Celkový prúd je:

I = v / r = 10 V / 5 Ω = 2 a

Tento prúd je rozdelený ako:

Jo_12Ω = (3/12) 2 a = 0.5 a

Preto napätie je:

Vložka_12Ω = 0.5 A × 12 Ω = 6 V

Teraz je zdroj aktivovaný₁:

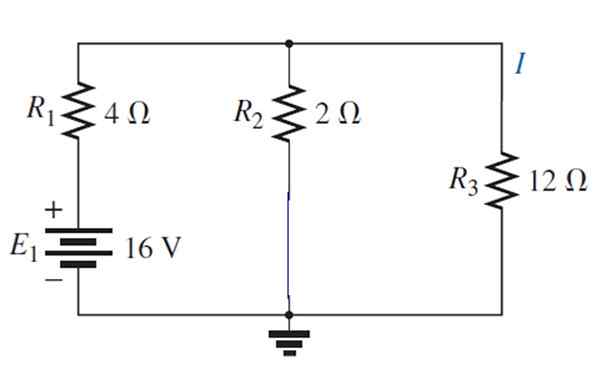
Výsledný obvod možno nakresliť týmto spôsobom:

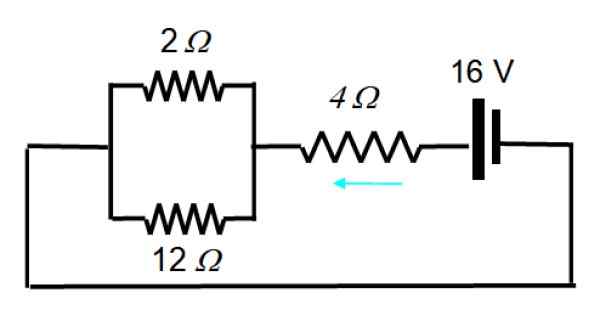
1/r_rovnica = (1/12) + (1/2) = 7/12 → r_rovnica = 12/7 Ω

A v sérii s 4 Ω Je to ekvivalentný odpor 40/7 Ω. V tomto prípade je celkový prúd:

I = v/r = 16 V/(40/7) Ω = 14/5 a

Deltátor napätia s týmito hodnotami sa znova uplatňuje:

Jo_12Ω = ((12/7)/12) (14/5) a = 0.4 a

Výsledný prúd je: 0.päťdesiat.4 a = 0.1 a. Všimnite si, že boli odpočítané, pretože prúd každého zdroja má iný význam, ako je vidieť na pôvodnom obvode.

Napätie prostredníctvom odporu je:

Vložka_12Ω = 0.4 A × 12 Ω = 4.8 V

Nakoniec celkové napätie je: 6 V-4.8 v = 1.2 v

Odkazy

1. Alexander, C. 2006. Základy elektrických obvodov. Tretí. Vydanie. MC Graw Hill.
2. Boylestad, r. 2011. Úvod do analýzy obvodu. Druhý. Vydanie. Pearson.
3. Dorf, r. 2006. Úvod do elektrických okruhov. 7. Vydanie. John Wiley & Sons.
4. Edminister, J. Devätnásť deväťdesiat šiestich. Elektrické obvody. Séria Schaum. Tretí. Vydanie. MC Graw Hill
5. Wikipedia. Súčasný deliteľ. Obnovené z: Je to.Wikipedia.orgán.