Vlastnosti ortogonálnej matrice, demonštrácia, príklady

Máte jedného Ortogonálna matica Ak je uvedená matica vynásobená jej transpozíciou, má výsledky v matrici identity. Ak je inverzia matrice rovná transponovanej, potom je pôvodná matica ortogonálna.

Ortogonálne matice sú charakteristické, že počet riadkov sa rovná počtu stĺpcov. Okrem toho sú riadkové vektory jednotkové ortogonálne vektory a vyrážky transponovaných vektorov sú tiež.

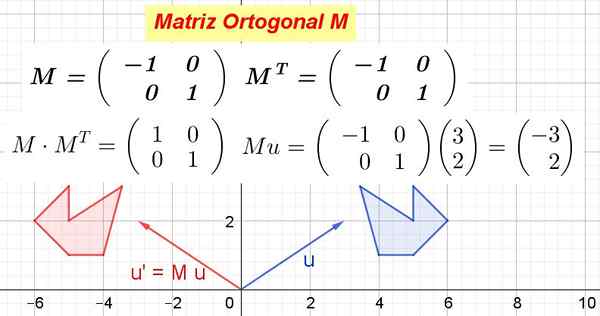postava 1. Príklad ortogonálnej matrice a ako transformuje geometrické objekty. (Pripravil Ricardo Pérez)

Keď sa ortogonálna matica vynásobí vektormi vektorového priestoru, vytvorí sa izometrická transformácia, to znamená transformácia, ktorá nemení vzdialenosti a zachováva uhly.

Typickým zástupcom ortogonálnych matíc je matice rotácie. Transformácie ortogonálnych matíc na vektorovom priestore sa nazývajú Ortogonálne transformácie.

Geometrické transformácie rotácie a odraz bodov predstavovaných jeho karteziánskymi vektormi sa uskutočňujú použitím ortogonálnych matíc na pôvodných vektoroch, aby sa získali súradnice transformovaných vektorov. Z tohto dôvodu sa ortogonálne matice široko používajú pri výpočtovom grafickom spracovaní.

[TOC]

Vlastnosti

Pole M Je ortogonálny, ak sa vynásobí jeho transpozíciou M^Tón matica identity vedie k Jo. Podobne produkt transpozície ortogonálnej matrice pôvodnou maticou matice identity:

M m^Tón = M^Tón M = i

V dôsledku predchádzajúceho vyhlásenia sa transponovaná ortogonálna matica rovná jej inverznej matici:

M^Tón = M^-1.

Sada matíc ortogonálnych rozmerov n x n Tvoria ortogonálnu skupinu Alebo (n). A podskupina Alebo (n) ortogonálnych matíc s určovaním +1 Špeciálna matica skupina jej (n). Matice skupiny Tvoj (n) Sú to matrice, ktoré vytvárajú lineárne transformácie rotácie, známe tiež ako Rotácia.

Demonštrácia

Ukážeme, že matica je ortogonálna, ak a iba vtedy, ak sú riadkové vektory (alebo stĺpcové vektory) ortogonálne navzájom a z normy 1.

Môže vám slúžiť: Bayesova veta

Predpokladajme, že rady ortogonálnej matice n x n sú ortonormálne vektory dimenzie n. Ak je označený vložka1, vložka2,.. ., vložkan Vektory sú splnené:

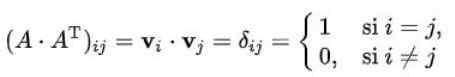
Kde je zrejmé, že sada riadkových vektorov je sada ortogonálnych vektorov s normou.

Príklady

Príklad 1

Ukážte, že matica 2 x 2, ktorú má vektor vo svojom prvom riadku V1= (-1 0) a vo svojom druhom riadku vektor V2= (0 1) je ortogonálna matica.

Riešenie: Matica je postavená M a jeho transpozícia sa vypočíta M^Tón:

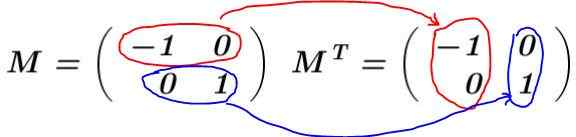
V tomto príklade matica M Je to transponované auto, to znamená, že matica a jej transpozícia sú rovnaké. Znásobuje sa M za jeho transponovanie M^Tón:

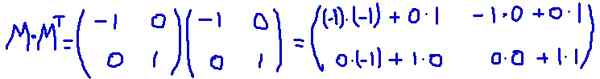
To sa overuje M M^Tón Rovná sa matici identity:

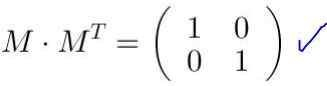
Keď matica M Vynásobí sa súradnicami vektora alebo bodu, získané nové súradnice, ktoré zodpovedajú transformácii, ktorú matrica vytvára na vektore alebo bode.

Obrázok 1 ukazuje ako M Transformuje vektor alebo v alebo ' A tiež rád M Transformujte modrý mnohouholník na červený mnohouholník. Ako M Je to ortogonálne, potom je to ortogonálna transformácia, ktorá zachováva vzdialenosti a uhly.

Príklad 2

Predpokladajme, že máte maticu 2 x 2 definovanú v Reais danej nasledujúcim výrazom:

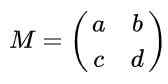
Nájdite skutočné hodnoty do, b, c a d takže matica M Byť ortogonálnou maticou.

Riešenie: Podľa definície je matica ortogonálna, ak sa vynásobí jeho transpozíciou v dôsledku toho matica identity. Pamätajte si, že transponovaná matica sa získa z pôvodného, ​​výmena riadkov podľa stĺpcov je nasledujúca rovnosť:

Môže vám slúžiť: doména a rozpory funkcie (s príkladmi)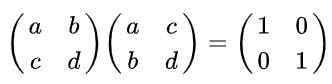

Vykonanie násobenia matrice je:

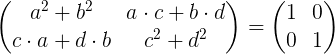
Rovnakom prvkov ľavej matice s prvkami matice identity vpravo, získame systém štyroch rovníc so štyrmi neznámymi A, B, C a D.

Navrhujeme pre A, B, C a D nasledujúce výrazy založené na trigonometrických dôvodoch Sinus a Cosine:

S týmto návrhom a kvôli základnej trigonometrickej identite sa automaticky uspokojí prvá a tretia rovnica rovnosti prvkov matrice. Tretia a štvrtá rovnica je rovnaká a v maticovej rovnosti po nahradení navrhovaných hodnôt je takáto:

Čo vedie k nasledujúcemu riešeniu:

Nakoniec sa pre ortogonálnu maticu M získajú nasledujúce roztoky:

Všimnite si, že prvý z riešení má determinant +1, takže patrí do jej skupiny (2), zatiaľ čo druhé riešenie má determinant -1, a preto nepatrí do tejto skupiny.

Príklad 3

Vzhľadom na nasledujúcu maticu nájdite hodnoty A a B, ktoré majú ortogonálnu maticu.

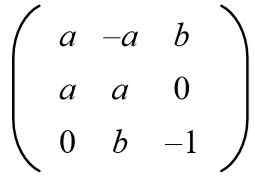
Riešenie: Aby bola daná matica ortogonálna, výrobok s jeho transpozíciou musí byť matica identity. Potom je maticový produkt matrice uvedenej s jej transponovanou maticou, ktorá dáva nasledujúci výsledok:

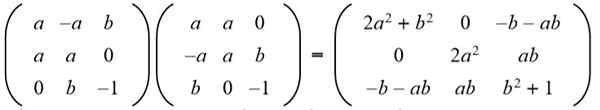
Ďalej je výsledok zladený s maticou identity 3 x 3:

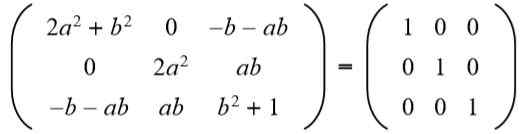
V treťom stĺpci druhého riadku, ktorý máte (A b = 0), ale do Nemôže to byť nula, pretože ak áno, rovnosť prvkov druhého riadku a druhého stĺpca by sa nesplnila. Potom nevyhnutne B = 0. Výmena b Pre hodnotu 0 máme:

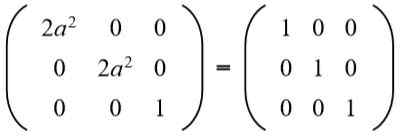
Potom sa rovnica vyrieši: 2A^2 = 1, ktorých riešenia sú: +½ štvrte 2 a -½√2.

Môže vám slúžiť: typy uhlov, charakteristík a príklady

Berie pozitívne riešenie na do Výsledkom je nasledujúca ortogonálna matica:

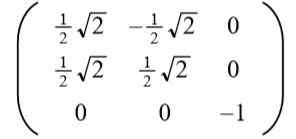
Čitateľ môže ľahko overiť, či sú riadky (a tiež stĺpčné vektory) ortogonálne a jednotky, to znamená ortonormálne.

Príklad 4

Preukázať, že matica Do ktorých riadky sú V1 = (0, -1 0), V2 = (1, 0, 0) a V3 = (0 0 -1) Je to ortogonálna matica. Okrem toho zistite, ako sa transformujú vektory kanonickej základne I J K Do vektorov U1, U2 a U3.

Riešenie: Malo by sa pamätať na to, že prvok (i, j) matrice vynásobenej jej transpozíciou je skalárny produkt vektora riadku (i) stĺpcom (j) transpozície. Okrem toho sa tento produkt rovná Kroneckerovej delte v prípade, že je matica ortogonálna:

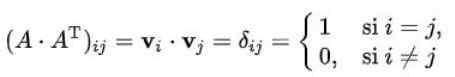
V našom prípade je to takto:

V1 • v1 = 0x0 + (-1) x (-1) + 0x0 = 1

V2 • v2 = 1 × 1 + 0x0 + 0x0 = 1

V3 • v3 = 0x0 + 0x0 + (-1) x (-1) = 1

V1 • v2 = 0x1 + (-1) x0 + 0x0 = 0

V2 • v1 = 1 × 0 + 0x (-1) + 0x0 = 0

V2 • v3 = 1 × 0 + 0x (0) + 0x (-1) = 0

V3 • v2 = 0x1 + 0x (0) + (-1) x0 = 0

V1 • v3 = 0x0 + (-1) x (0) + 0x (-1) = 0

V3 • v1 = 0x0 + 0x (-1) + (-1) x0 = 0

S tým, čo sa demonštruje, že ide o ortogonálnu maticu.

Okrem u1 = a i = (0, 1, 0); U2 = a j = (-1, 0, 0) a nakoniec U3 = a K = (0, 0, -1)

Odkazy

1. Anthony Nicolaides (1994) Determinanty a matice. Publikácia.
2. Birkhoff a Maclane. (1980). Modern Algebra, ed. Vicens-Vves, Madrid.
3. Casteleiro Villalba m.  (2004) Úvod do lineárnej algebry. Redakcia.
4. Dave Kirkby (2004) Maths Connect. Výtvarník.
5. Jenny Olive (1998) Maths: Sprievodca prežitím študenta. Cambridge University Press.
6. Richard J. Brown (2012) 30-sekundová matematika: 50 najvýznamnejších teórií matematiky. Ivy Press Limited.
7. Wikipedia. Ortogonálna matica. Obnovené z: je.Wikipedia.com
8. Wikipedia. Ortogonálna matica. Zdroj: In.Wikipedia.com