Popis, Aplikácie, príklady a cvičenia Norton

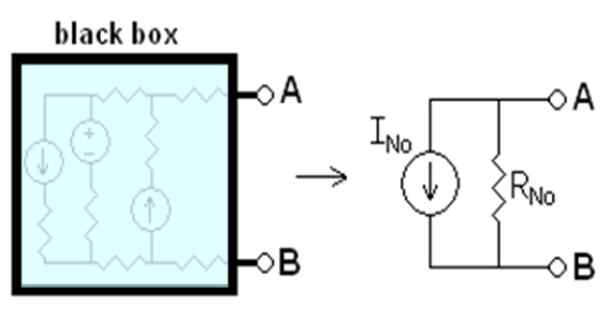
On Nortonova veta, ktorý sa vzťahuje na elektrické obvody, ustanovuje sa, že lineárny obvod s dvoma terminálmi A a B je možné nahradiť iným úplne ekvivalentom, pozostávajúcim zo prúdového zdroja s názvom I_Nie spojené paralelne s odporom r_Nie.

Povedal súčasný i_Nie počul som_N Je to ten, ktorý by prúdil medzi bodmi A a B, ak by boli krátke obvody. Odpor r_N Je to ekvivalentný odpor medzi terminálmi, keď sú deaktivované všetky nezávislé zdroje. Všetko povedané je schematizované na obrázku 1.

postava 1. Nortonov rovnocenný obvod. Zdroj: Wikimedia Commons. Brumkid [CC BY-SA 3.0 (http: // creativeCommons.Org/licencie/By-SA/3.0/]]

Čierna skrinka na obrázku obsahuje lineárny obvod, ktorý bude nahradený jeho ekvivalentom Norton. Lineárny obvod je ten, v ktorom majú vstup a výstup lineárna závislosť, ako napríklad vzťah medzi napätím V a priamym prúdom I v Ohmic Element: V = I.R.

Tento výraz zodpovedá Ohmovmu zákonu, kde R je odpor, ktorý môže byť tiež impedanciou, ak ide o striedavý prúdový obvod.

Nortonova veta bola vyvinutá elektrotechnickým a vynálezcom Edward L Engineer. Norton (1898-1983), ktorý dlho pracoval pre Bell Laboratories.

[TOC]

Aplikácie Nortonovej vety

Ak majú veľmi komplikované siete, s mnohými odpormi alebo impedanciami a chcete menší a zvládnuteľný obvod.

Týmto spôsobom je Nortonova veta veľmi dôležitá pri navrhovaní obvodov s viacerými prvkami, ako aj pre štúdium ich reakcie.

Vzťah medzi Nortonom a The Theveninovými vetami

Nortonova veta je Dual Theveninova veta, čo znamená, že sú rovnocenní. Theveninova veta naznačuje, že čierna skrinka na obrázku 1 sa dá nahradiť zdrojom napätia série s odporom nazývanom Thevenin R Resistance_Th. Toto je vyjadrené na nasledujúcom obrázku:

Môže vám slúžiť: Materiálová mechanika: História, oblasť štúdia, aplikácie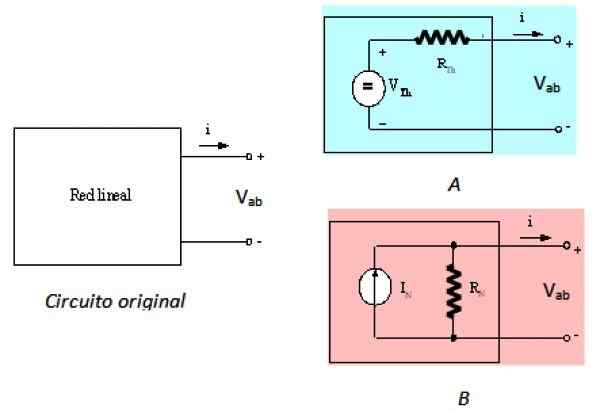 Obrázok 2. Pôvodný ľavý okruh a jeho ekvivalenty od Thévenina a Nortona. Zdroj: f. Zapata.

Ľavý obvod je pôvodný obvod, lineárna sieť v čiernej skrinke, obvod doprava je ekvivalentom Thevenina a obvodu B Je to Nortonov ekvivalent, ako je opísané. Z terminálov A a B, tri obvody sú rovnocenné.

Teraz to pozorujte:

-V pôvodnom obvode je napätie medzi terminálmi V_AB.

-Vložka_AB  = V_Th v okruhu Do

-Nakoniec, v_AB  = I_N.R_N v okruhu B

Ak sú terminály A a B skrat v troch obvodoch, musí sa splniť, že napätie a prúd medzi týmito bodmi musia byť rovnaké pre tri, pretože sú ekvivalentné. Tak:

-V pôvodnom obvode je prúd i.

-Pre obvod A je prúd i = v_Th / R_Th, Podľa Ohmovho zákona.

-Nakoniec v okruhu B, prúd je i_N

Preto sa dospelo k záveru, že odpor Norton a Thevenin majú rovnakú hodnotu a že prúd je daný:

i = i_N = V_Th / R_Th = V_Th / R_N

Príklad

Ak chcete správne aplikovať Nortonovu vetu, dodržiavajú sa nasledujúce kroky:

-Sekcia obvodu, pre ktorú bude ekvivalent Nortonu nájdený zo siete, je izolát zo siete.

-V zostávajúcom obvode uveďte terminály A a B.

-Vymeňte zdroje napätia skratovými obvodmi a prúdmi za otvorené obvody, aby ste našli ekvivalentný odpor medzi terminálmi A a B. Toto je r_N.

-Vráťte všetky zdroje do svojich pôvodných pozícií, skratka -obvod terminálov A a B a nájdite prúd, ktorý medzi nimi cirkuluje. Toto som ja_N.

Môže vám slúžiť: Doppler Effect: Popis, vzorce, prípady, príklady

-Nakreslite Nortonov ekvivalentný obvod podľa toho, čo je uvedené na obrázku 1. Prúdový zdroj a ekvivalentný odpor sú paralelne.

Môžete tiež použiť Theveninovu vetu, aby ste našli r_Th, že už vieme, že sa rovná R_N, Potom Ohmovým zákonom nájdete i_N A výsledný obvod je nakreslený.

A teraz sa pozrime na príklad:

Nájdite ekvivalent Nortona medzi bodmi A a B nasledujúceho obvodu:

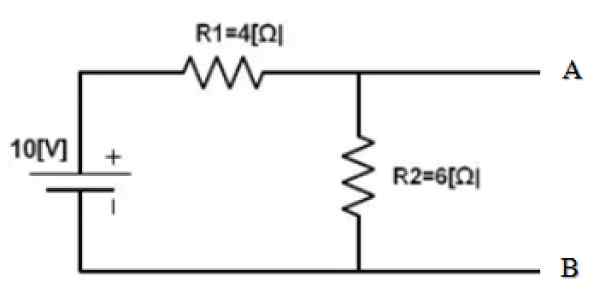Obrázok 3. Obvod. Zdroj: f. Zapata.

Časť okruhu je už izolovaná, ktorej ekvivalent sa musí nájsť. A body A a B sú jasne určené. Nasleduje skrat o zdroji 10 V a nájdenie ekvivalentného odporu získaného obvodu:

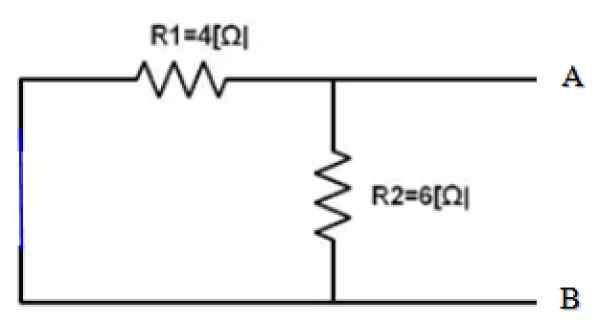Obrázok 4. Skrutkový zdroj. Zdroj: f. Zapata.

Pohľady z terminálov A a B, obidve odpory r₁ a r₂ Sú preto paralelne:

1/r_rovnica = 1/r₁₂ = (1/4) + (1/6) Ω^-1 = 5/12 Ω^-1  → R_rovnica = 12/5 Ω = 2.4 Ω

Potom sa zdroj vráti na svoje miesto a body A a B sú krátke obvody, aby sa našli prúd, ktorý sa tam cirkuluje, to bude_N. V tom prípade:

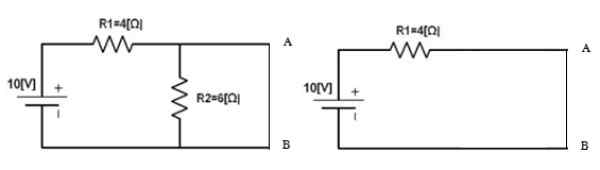Obrázok 5. Obvod na výpočet prúdu Norton. Zdroj: f. Zapata.

Jo_N = 10 V / 4 Ω = 2.5 a

Nortonov ekvivalent

Nakoniec je Nortonov ekvivalent s nájdenými hodnotami nakreslený:

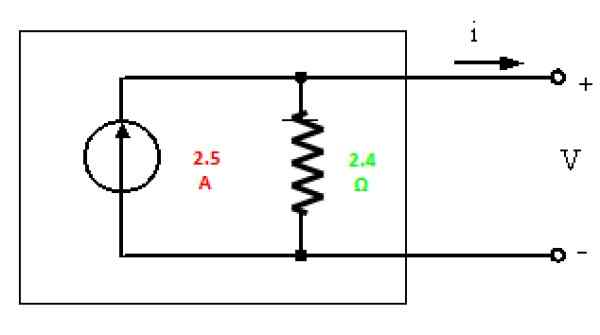Obrázok 6. Norton ekvivalent obvodu na obrázku 3. Zdroj: f. Zapata.

Cvičenie

Na obvode nasledujúceho obrázku:

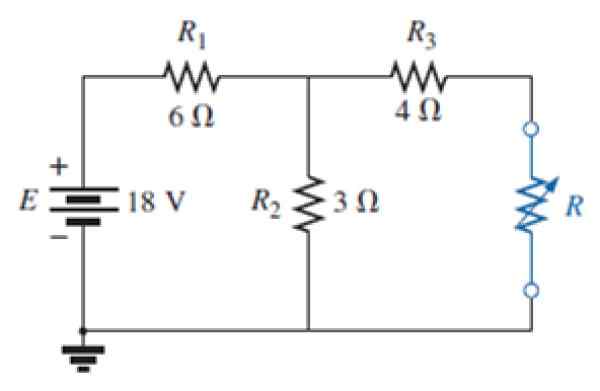Obrázok 7. Obvod pre cvičenie vyriešené. Zdroj: Alexander, C. 2006. Základy elektrických obvodov. Tretí. Vydanie. MC Graw Hill.

a) Nájdite ekvivalentný obvod Nortonovej siete odporu vonkajšej modrej.

b) tiež nájdite Théveninov ekvivalent.

Roztok

Podľa vyššie uvedených krokov musí byť zdroj krátky obvod:

Môže vám slúžiť: Difrakcia zvuku: Čo pozostáva z príkladov, aplikácií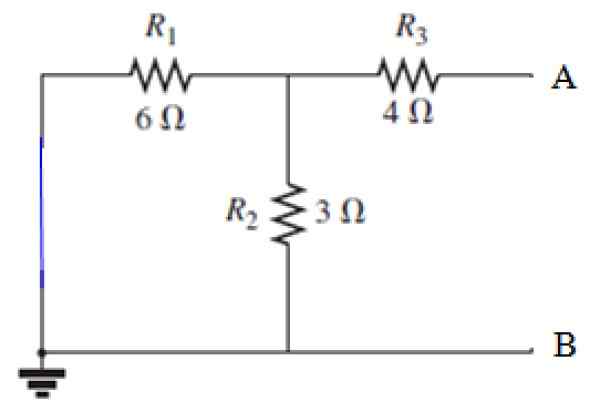 Obrázok 8. Zdroj krátkych obvodov v obvode na obrázku 7. Zdroj: f. Zapata.

Výpočet

Pohľad z terminálov A a B, odpor R₃ je v sérii s paralelnou tvorbou odporov r₁ a r₂, Najprv vypočítame ekvivalentný odpor tohto paralelu:

1/r₁₂ = (1/6)+ (1/3) Ω^-1 = 1/2 Ω^-1  → R_rovnica = 2/1 Ω = 2Ω

A potom je táto paralela v sérii s R_3, takže ekvivalentný odpor je:

R_rovnica = 2 Ω + 4 Ω = 6 Ω

Toto je hodnota oboch r_N od r_Th, Ako už bolo vysvetlené predtým.

Výpočet

Potom sú terminály A a B krátke obvody, ktoré vrátia zdroj na svoje miesto:

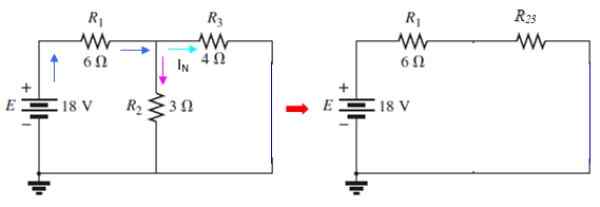Obrázok 9. Obvody prúdu Norton. Zdroj: f. Zapata.

Súčasný prechádzajúci cez I₃ je aktuálny i_N hľadaný, ktorý je možné určiť metódou ôk alebo pomocou série a paralelne. V tomto obvode r₂ a r₃ Sú paralelne:

1/r₂₃ = (1/3)+ (1/4) Ω^-1 = 7/12 Ω^-1  → R₂₃ = 12/7 Ω

Odpor r₁ Je v sérii s touto paralelnou, potom:

R₁₂₃ = 6 + (12/7) Ω = 54/7 Ω

Prúd, ktorý vychádza zo zdroja (modrá farba), sa počíta podľa Ohmovho zákona:

V = i. R → i = v/r = 18 V/(54/7 Ω) = 7/3 a

Tento prúd je rozdelený na dve časti: jedna, ktorá prechádza r₂ A ďalší, ktorý prechádza r₃. Prúd, ktorý prechádza paralelnou r₂₃ To isté prechádza r₁, ako je vidieť na strednom obvode obrázku. Napätie je:

Vložka₂₃ = I.R₂₃ = (7/3) a .(12/7) Ω = 4 V

Oba odpory r₂ a r₃ Sú na tomto napätí, pretože sú teda paralelne:

Jo₃ = V₂₃ / R₃ = 4 V / 4 Ω = 1 a

Už máme hľadaný prúd Norton, pretože som už povedal, že som₃ = I_N, tak:

Jo_N = 1 a

Nortonov ekvivalent

Všetko je pripravené nakresliť ekvivalent tohto obvodu Norton medzi bodmi A a B:

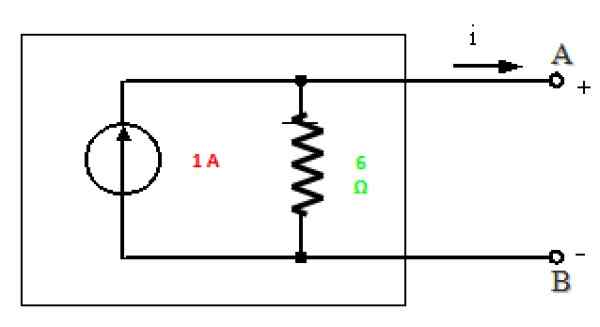Obrázok 10. Norton ekvivalent obvodu na obrázku 7. Zdroj: f. Zapata.

Riešenie B

Nájdenie Théveninovho ekvivalentu je veľmi jednoduché, pretože r_Th = R_N= 6 Ω a ako je vysvetlené v predchádzajúcich častiach:

Vložka_Th = I_N. R_N = 1 a . 6 Ω = 6 V

Théveninov ekvivalentný obvod je:

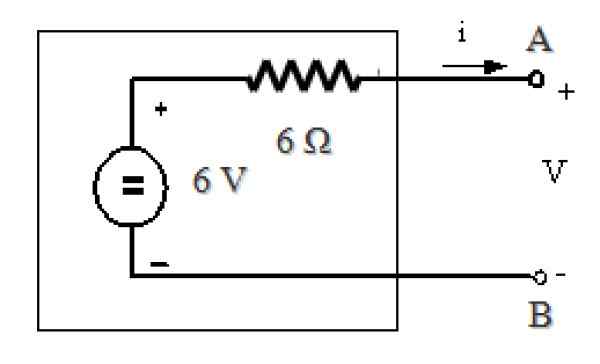Obrázok 11. Theveninov ekvivalent obvodu na obrázku 7. Zdroj: f. Zapata.

Odkazy

1. Alexander, C. 2006. Základy elektrických obvodov. Tretí. Vydanie. MC Graw Hill.
2. Boylestad, r. 2011. Úvod do analýzy obvodu. Druhý. Vydanie. Pearson.
3. Dorf, r. 2006. Úvod do elektrických okruhov. 7. Vydanie. John Wiley & Sons.
4. Edminister, J. Devätnásť deväťdesiat šiestich. Elektrické obvody. Séria Schaum. Tretí. Vydanie. MC Graw Hill.
5. Wikipedia. Nortonova veta . Obnovené z: Je to.Wikipedia.orgán.