Lano (geometria) dĺžka, veta a cvičenia

A lano, V plochej geometrii je to segment čiary, ktorý spája dva body z krivky. Hovorí sa, že čiara obsahujúca tento segment je sušiacim riadkom krivky. Je to často obvod, ale určite môžete nakresliť reťazce do mnohých ďalších kriviek, ako sú elipsy a podobenstvá.

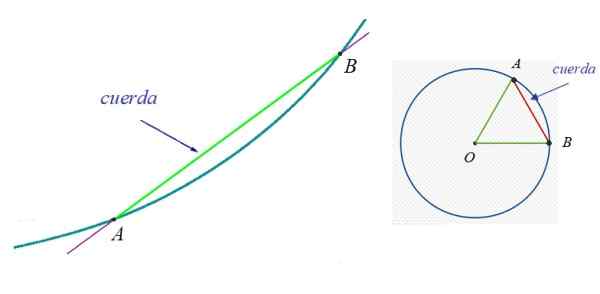
Na obrázku 1 vľavo je krivka, do ktorej patria body A a B. Lano medzi A a B je zelený segment. Napravo je obvod a jeden z ich reťazcov, pretože je možné sledovať nekonečné.

postava 1. Vľavo lano ľubovoľnej krivky a doprava lano kruhu. Zdroj: Wikimedia Commons.

V obvode je jeho priemer obzvlášť zaujímavý, čo je tiež známe ako Hlavné lano. Je to lano, ktoré vždy obsahuje stred obvodu a meria dvakrát polomer.

Nasledujúce číslo je znázornené polomerom, priemerom, lanom a tiež oblúkom kruhu. Pri riešení problémov je dôležitá správne identifikovať každú z nich.

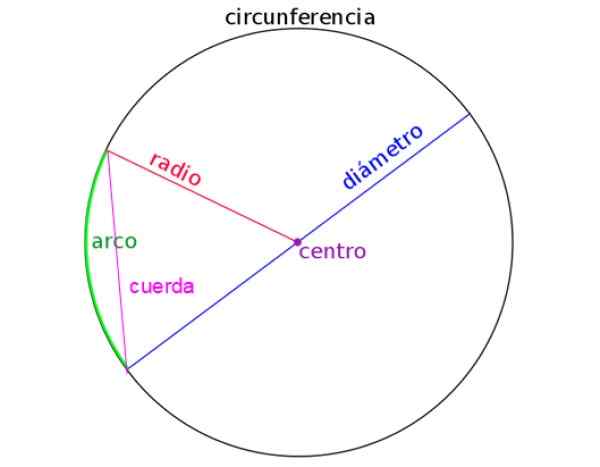Obrázok 2. Prvky obvodu. Zdroj: Wikimedia Commons.

[TOC]

Dĺžka lana obvodu

Môžeme vypočítať dĺžku lana v kruhu začínajúc z obrázkov 3A a 3B. Všimnite si, že trojuholník je vždy tvorený dvoma rovnakými stranami (izosceles): segmenty OA a OB, ktoré merajú R, polomer obvodu. Tretia strana trojuholníka je segment AB, nazývaný C, čo je presne dĺžka lana.

Je potrebné nakresliť čiaru kolmú na lano C, aby sa rozdelilo v uhle 9, ktorý existuje medzi dvoma rádiá a ktorých vrcholom je stred alebo obvod. Toto je centrálny uhol -Pretože jeho vrchol je stredná a bisektorová čiara je tiež sekundou obvodu.

Môže vám slúžiť: radikálne vlastnosti

Okamžite sa vytvoria dva obdĺžniky, ktorých hypotenus. Pretože priemer a s ním priemer sa delí na dve časti rovnajúce sa lane, ukázalo sa, že jedna z nôh je polovica C, ako je uvedené na obrázku 3B.

Z definície prsníka uhla:

sin (9/2) = oproti/hypotenusa cateto = (c/2)/r

Preto:

Sin (9/2) = C/2R

C = 2R Sen (9/2)

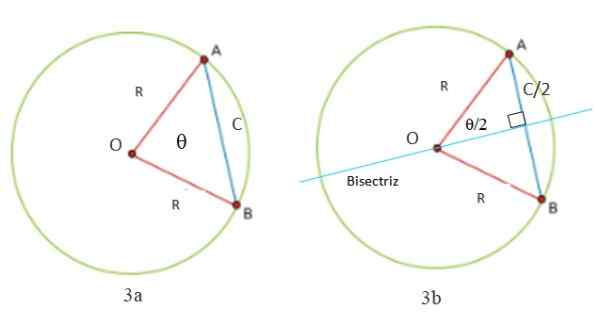Obrázok 3. Trojuholník tvorený dvoma rádiámi a obvodovým lanom je izoscely (obrázok 3), pretože má dve strany rovnaké. Bisektor ho rozdeľuje na dva trojuholníky obdĺžnikov (obrázok 3B). Zdroj: Pripravený F. Zapata.

Veta 

Veta reťazca hovorí:

Ak sa v jednom bode pretína akékoľvek dve laná, produkt dĺžky segmentov, ktoré sa objavujú na jednom zo reťazcov, sa rovná produktu dĺžok segmentov, ktoré sú definované v druhom lane.

Nasledujúci obrázok zobrazuje dva reťazce toho istého obvodu: AB a CD, ktoré sa pretína v bode P. V lane AB sú definované segmenty AP a PB, zatiaľ čo CP a PD sú definované v lane CD. Potom podľa vety:

AP . Pb = cp . P.S

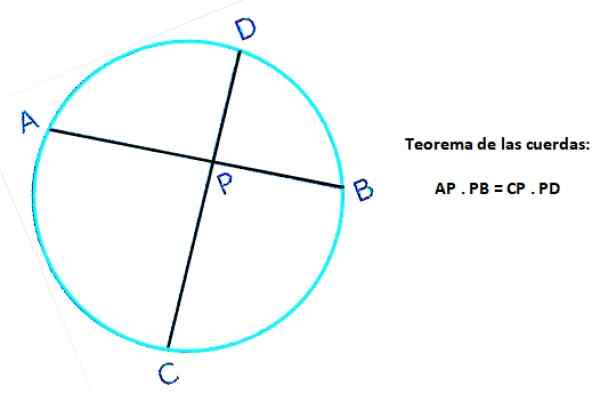Obrázok 4. Lano veta obvodu. Zdroj: f. Zapata.

Vyriešené reťazce cvičení

- Cvičenie 1

Kruh má 48 cm lano, ktoré je 7 cm od stredu. Vypočítajte oblasť kruhu a obvod obvodu.

Riešenie  

Na výpočet kruhu v oblasti stačí poznať polomer obvodu na štvorec, pretože je splnený:

A = π.R²

Teraz je obrázok, ktorý je tvorený poskytnutými údajmi, obdĺžnikový trojuholník, ktorého nohy sú 7 a 24 cm.

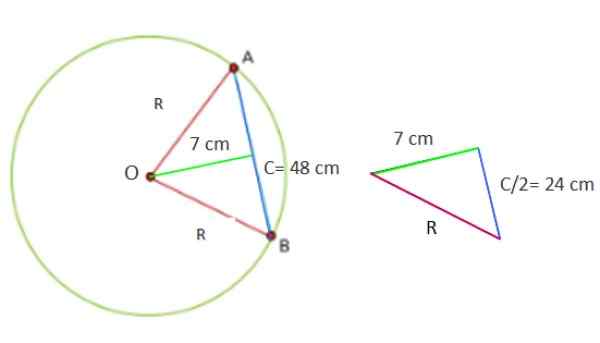Obrázok 5. Geometria pre vyriešené cvičenie 1. Zdroj: f. Zapata.

Preto nájsť hodnotu R² Veta Pythagoras C sa aplikuje priamo² = a² + b², Pretože R je hypotenus trojuholníka:

Môže vám slúžiť: Nulový uhol: Definícia a charakteristiky, príklady, cvičenia

R² = (7 cm)² + (24 cm)² = 625 cm²

Potom požadovaná oblasť je:

A = π. 625 cm² = 1963.5 cm²

Pokiaľ ide o obvod alebo dĺžku L obvodu, vypočíta sa podľa:

L = 2π. R

Výmena hodnôt:

R = √625 cm² = 25 cm

L = 2π. 25 cm = 157.1 cm.

- Cvičenie 2

Určite dĺžku lana kruhu, ktorého rovnica je:

X² + a² - 6x - 14y -111 = 0

Je známe, že súradnice stredu lana sú P (17/2; 7/2).

Riešenie

Stred P lana nepatrí do obvodu, ale extrémne body lana áno. Problém je možné vyriešiť pomocou predtým uvedenej vety reťazcov, ale najskôr je to vhodné.

Krok 1: Získajte kanonickú rovnicu obvodu

Kanonická rovnica obvodu so stredom (H, k) je:

(X-H)² + (Y-k)² = R²

Na jeho získanie je potrebné dokončiť štvorce:

(X² - 6x) + (a² - 14y) -111 = 0

Všimnite si, že 6x = 2.(3x) a 14y = 2.(7y), takže predchádzajúci výraz je prepísaný, takže sa nezmení:

(X² - 6x+3²-3²) + (a² - 14y+7²-7²) -111 = 0

A teraz si pamätáte na definíciu pozoruhodného produktu (A-B)² = a² - 2ab + b² Dá sa napísať:

(X - 3)² - 3² + (a - 7)² - 7² - 111 = 0

= (x - 3)² + (a - 7)² = 111 + 3² + 7² → (x - 3)² + (a - 7)² = 169

Obvod má stred (3,7) a rádio r = √169 = 13. Nasledujúci obrázok zobrazuje graf obvodu a reťazce, ktoré sa použijú v vete:

Môže vám slúžiť: Aké sú 7 prvkov obvodu?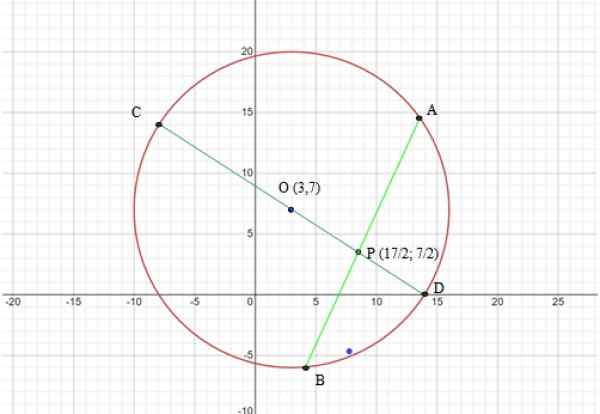Obrázok 6. Graf obvodu cvičenia vyriešil 2. Zdroj: f. Zapata prostredníctvom online grafickej kalkulačky matematiky.

Krok 2: Určite segmenty, ktoré sa majú použiť v vete reťazca

Segmenty, ktoré sa majú použiť, sú reťazce CD a AB, podľa obrázku 6, sú oba rezané v bode P, preto:

Cp . PD = AP. Pb

Teraz sa chystáme nájsť vzdialenosť medzi bodmi O a P, pretože nám to dá dĺžku segmentu OP. Ak do tejto dĺžky pridáme polomer, budeme mať segment CP.

Vzdialenosť d_Oproti Medzi dvoma súradnicovými bodmi (x₁,a₁) a (x₂,a₂) je:

d_Oproti² = Op² = (x₂ - X₁)² + (a₂ - a₁)² = (3- 17/2)² + (7-7/2)² = 121/4 + 49/4 = 170/4

d_Oproti = Op = √170 /2

So všetkými získanými výsledkami a grafom zostavíme nasledujúci zoznam segmentov (pozri obrázok 6):

CO = 13 cm = r

OP = √170 /2 cm

CP = OP + R = 13 + √170 /2 cm

PD = OD - OP = 13 - √170 /2 cm

AP = PB

2.AP = dĺžka lana

Výmena v vete reťazca:

Cp . PD = AP . Pb = [(13 +√170 /2) . (13 -√170 /2)] = AP²

[169-170/4] = AP²

253/2 = AP²

AP = √ (253/2)

Dĺžka lana je 2.AP = 2 (√253/2) = √506

Mohol čitateľ vyriešiť problém iným spôsobom?

Odkazy

1. Baldor, a. 2004. Geometria plochej a vesmíru s trigonometriou. Kultúrne publikácie s.Do. c.Vložka. Mexiko.
2. C-K12. Potrubie. Získané z: CK12.orgán.
3. Escobar, J. Obvod. Obnovené z: matematiky.vy.Edu.co.
4. Villena, m. Kužeľový. Zdroj: DSPACE.Espol.Edu.ES.
5. Wikipedia. Lano (geometria). Obnovené z: je.Wikipedia.orgán.