Zelená veta, demonštrácia, aplikácie a cvičenia

On Zelená veta Je to metóda výpočtu, ktorá sa používa na prepojenie integrálov liniek s dvojitou plochou alebo povrchovou integrálmi. Zainteresované funkcie musia byť označené ako vektorové a definované polia v trajektórii C.

Napríklad výraz integrálnej línie môže byť veľmi komplikovaný na riešenie; Pri implementácii Green's Theorém sa však stanú dvojitými integrálmi celkom základnými. Vždy je dôležité rešpektovať pozitívny zmysel pre trajektóriu, to sa týka smeru hodinových ihiel.

Greenova veta je osobitným prípadom Stokesovej vety, kde sa projekcia vektorovej funkcie vykonáva v rovine XY.

[TOC]

Definícia

Greenov výraz Greenovej vety je nasledujúci:

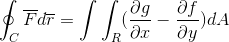
V prvom termíne je pozorovaný integrál riadku definovanej trajektóriom „C“, z skalárneho produktu medzi vektorovou funkciou „F“ a funkciou vektora „r“.

C: Je to definovaná trajektória, na ktorej sa vektorová funkcia premieta, pokiaľ bude definovaná pre túto rovinu.

F: Vektorová funkcia, kde je každá z jeho komponentov definovaná funkciou ako taká (F, G).

Odpoveď: Je to vektor tangens do oblasti R, na ktorej je integrál definovaný. V tomto prípade sa prevádzkuje s rozdielom tohto vektora.

V druhom funkčnom období vidíme, ako sa Green vyvinula veta, kde sa pozoruje dvojitý integrál definovaný v oblasti R rozdielu čiastočných derivátov G a F, vzhľadom na X a a respektíve. Pre diferenciál oblasti, ktorý nie je ničím iným ako produktom oboch dvoch dimenzionálnych diferenciálov (DX.D Y).

Táto veta je dokonale použiteľná pre priestorové a povrchové integrály.

Demonštrácia

Aby ste ukázali Greenovu vetu jednoduchým spôsobom, táto úloha sa rozdelí na 2 časti. Najprv predpokladáme, že funkcia vektora F má iba definíciu vo Versor Jo. Zatiaľ čo funkcia „g“ zodpovedajúca Verorovi J bude sa rovnať nule.

Môže vám slúžiť: Koľko stotín sa zmestí do desiateho? (Príklady)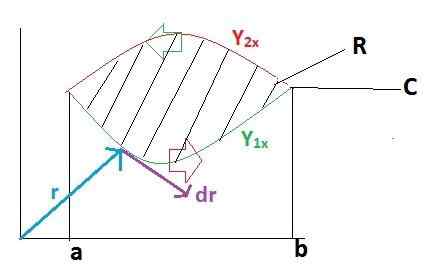Autor

F = f (x, y)Jo + G (x, y)J = f (x, y)Jo + 0

R = xJo + aJ

DR = DXJo + D YJ

Najprv rozvíjame integrál riadku po trajektórii C, pre ktorú bola trajektória odložená v 2 oddieloch, ktoré idú najprv z A do B a po B do a.

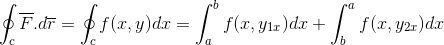
Uplatňuje sa definícia základnej vety výpočtu pre definovaný integrál.

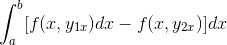
Výraz je usporiadaný v jednom integráli, je spoločný pre negatívne a poradie faktorov sa obráti.

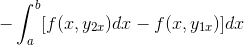
Podrobným pozorovaním tohto výrazu je zrejmé, že pri uplatňovaní kritérií primitívnej funkcie je v prítomnosti integrálu expresie odvodeného od f s ohľadom na a. Vyhodnotené v parametroch

[a_1x , a_2x]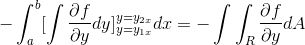

Teraz stačí predpokladať, že funkcia Vector Fun je definovaná iba pre G (x, y)J. Ak je pri prevádzke spôsobom homologovaný s predchádzajúcim prípadom, získa sa:

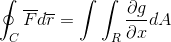
Nakoniec sa tieto dve demonštrácie prevezmú a pripojte sa v prípade, keď vektorová funkcia berie hodnoty pre oba Verors. Týmto spôsobom sa zobrazuje ako čiara integrál po definovaní a považovaní za jednosmernú trajektóriu, môže byť úplne vyvinutá pre lietadlo a priestor.

F = f (x, y)Jo + G (x, y)J

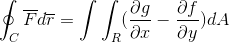
Týmto spôsobom sa demonštruje Greenova veta.

Žiadosti

Aplikácie zelenej vety sú široké v odvetviach fyziky a matematiky. Tieto sa rozširujú na akúkoľvek aplikáciu alebo použitie, ktoré je možné poskytnúť na integráciu riadkov.

Mechanická práca vykonaná silou F cez trajektóriu C sa môže vyvinúť pomocou integrálu línie, ktorá je vyjadrená ako dvojitý integrál oblasti cez Greenovu vetu.

Môže vám slúžiť: Pentagonálny hranol: Charakteristiky, časti, vrcholy, hrany, objem

Momenty zotrvačnosti mnohých orgánov vystavených externým silám v rôznych miestach aplikácie, tiež reagujú na vývojové integrály s Greenovou vetou.

To má viacero funkcií v štúdiách rezistencie materiálov, ktoré sa používajú. Kde je možné externé hodnoty kvantifikovať a zohľadniť pred vypracovaním rôznych prvkov.

Greenova veta vo všeobecnosti uľahčuje porozumenie a definíciu oblastí, v ktorých sú vektorové funkcie definované s ohľadom na oblasť podľa trajektórie.

História

Bola uverejnená v roku 1828 v práci Matematická analýza teórií elektriny a magnetizmu, napísal britský matematik George Green. Skúma celkom rozhodné oddiely pri uplatňovaní výpočtu vo fyzike, ako je koncept potenciálu, funkcie zelene a aplikácie jej automatickej vety s názvom.

George Green formalizoval svoju študentskú kariéru vo veku 40 rokov, doteraz úplne samostatný matematik bytia. Po štúdiu na University of Cambridge pokračuje jeho výskum a prispieva v oblasti akustiky, optiky a hydrodynamiky, ktoré sú dodnes v platnosti.

Vzťah s inými vetami

Greenova veta je špeciálny prípad a vyplýva z 2 ďalších veľmi dôležitých vety vo výpočtovej vetve. Toto je Kelvin-Stokesova veta a Divergencia alebo Gausskiova veta.

Od ktorejkoľvek z obidvoch teorémov môžete dosiahnuť Greenovu vetu. Na vývoj týchto demonštrácií sú potrebné určité definície a návrhy.

Cvičenia

- Nasledujúce cvičenie ukazuje, ako transformovať integrál čiary na dvojitý integrál vzhľadom na oblasť R.

Pôvodný výraz je nasledujúci:

Môže vám slúžiť: koľko stojí x?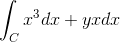

A musí sa vyhodnotiť v trojuholníkovej oblasti, ktorá spája body (0, 0), (1, 0), (0, 1) označené C. V tomto prípade sa bude brať do úvahy pozitívny zmysel pre otočenie.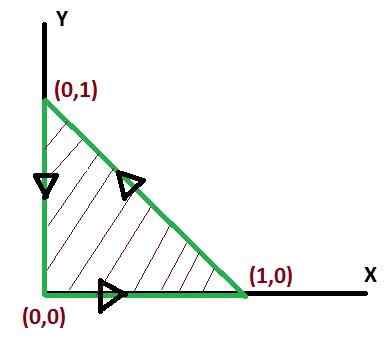

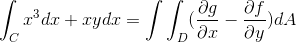
Odkiaľ sú funkcie zodpovedajúce f a g odobraté z

f (x, y) = x³                      g (x, y) = yx

df/dy = 0 dg/dx = y

Je dôležité definovať funkcie, ktoré tvoria limity oblasti C, aby bolo možné zostaviť diferenciálny produkt, ktorý bude úplne pokryť región.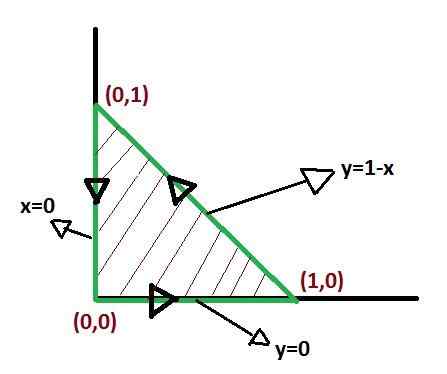

Pri aplikácii Greenovej vety neexistuje jedinečný spôsob, ako definovať limity integrácie. Existujú však formuláre, v ktorých môžu byť integrály po definovaní jednoduchšie. Takým spôsobom, že optimalizácia limitov integrácie si zaslúži pozornosť.

V tomto prípade sa tento výraz uvažuje: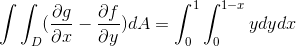

Kde pri riešení integrálov získame:

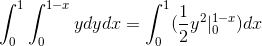
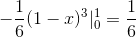
Táto hodnota zodpovedá v kubických jednotkách regiónu pod vektorovou funkciou a v trojuholníkovej oblasti definovanej C.

V prípade integrálu riadku bez vykonania zelenej metódy by bolo potrebné parametrizovať funkcie v každej časti regiónu. To znamená, že pre rozlíšenie urobte 3 parametrizované integrály. To je dostatočný dôkaz o účinnosti, ktorú Robert Green prispel k svojej vete k výpočtu.

Odkazy

1. Úvod do mechaniky kontinuu. W Michael Lai, David H. Rubin, Erhard Krempl, David Rubin Butterworth-Heinemann, 23. júla. 2009
2. Multivariabilný počet. James Stewart. Cengage Learning, 22. marca. 2011
3. Neformálna história Greenovej vety a súvisiace nápady. James Joseph Cross. Katedra matematiky, University of Melbourne, 1975
4. Tepelné správanie pomocou greenských funkcií. Kevin d. Cole, James V. Beck, a. Haji-Sheikh, Bahman Luckouhi. Taylor & Francis, 16. júla. 2010
5. Aplikácia Greenovej vety na extrémnizáciu lineárnych integrálov. Obranné technické informačné centrum, 1961