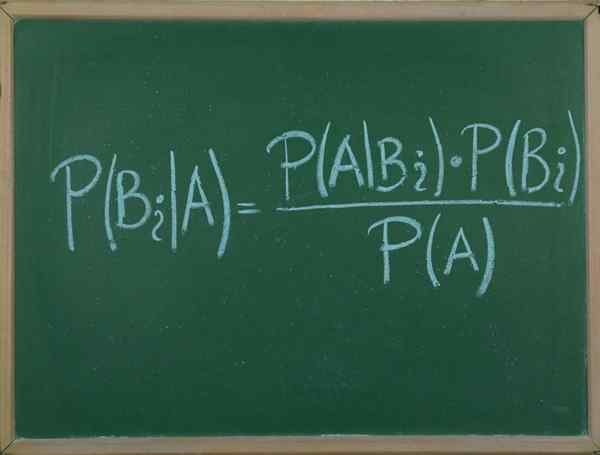Bayesova veta
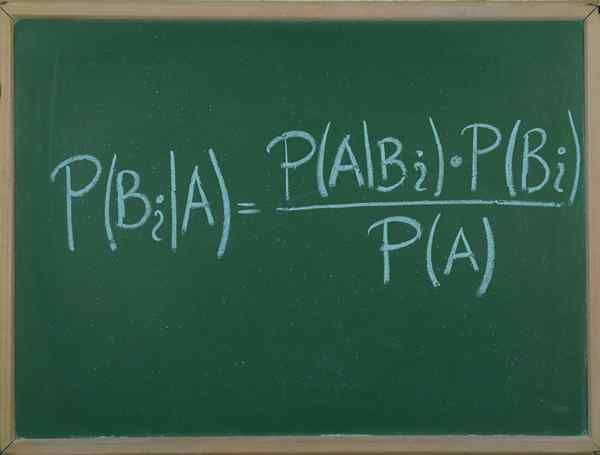
- 4543
- 1005
- Gabriel Bahna
Vysvetľujeme, čo je Bayesova veta, jej aplikácie a uvádzame vyriešené cvičenia
Čo je Bayesova veta?
On Bayesova veta Je to postup, ktorý nám umožňuje vyjadriť podmienenú pravdepodobnosť náhodnej udalosti a kocky B, pokiaľ ide o rozdelenie pravdepodobnosti danej udalosti B a rozdelenie pravdepodobnosti iba do.
Táto veta je veľmi užitočná, pretože vďaka nej môžeme súvisieť s pravdepodobnosťou, že udalosť A sa stane s vedomím, že sa odohráva B, s pravdepodobnosťou, že sa vyskytne opak, to znamená, že sa vyskytuje.
Bayesova veta bola striebornou návrhom reverenda Thomasa Bayesa, anglického teológa osemnásteho storočia, ktorý bol tiež matematikom. Bol autorom niekoľkých pracovných miest v teológii, ale v súčasnosti je známy pre niekoľko matematických zmlúv, medzi ktorými sa Bayesova veta už spomínala ako hlavný výsledok.
Bayes sa zaoberal touto vetou v diele s názvom „Esej o riešení problému v doktríne šancí“ (esej na riešenie problému v doktríne možností), publikovanej v roku 1763 a na ktorej veľké vyvinuli štúdie s aplikáciami s aplikáciami V rôznych oblastiach vedomostí.
Vysvetlenie
Po prvé, pre väčšiu kompresiu tejto vety sú potrebné niektoré základné pojmy teórie pravdepodobnosti, najmä veta násobenia pre podmienenú pravdepodobnosť, ktorá to ustanovuje
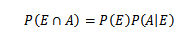
Pre e a ľubovoľné udalosti vzorového priestoru s.
A definícia oddielov, ktorá nám hovorí, že máme1 ,Do2,..., don udalosti vzorkovacieho priestoru, budú tvoriť oddiel S, ak aJo Sa vzájomne vylučujú a ich únia je S.
Môže vám slúžiť: Aké sú čísla pre? 8 hlavných použitíMať to, či už ide o ďalšiu udalosť. Takže vidíme B ako
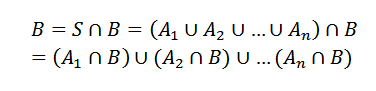
KdeJo Prehliadnuté s B sú vzájomne sa vylučujúce udalosti.
Av to,
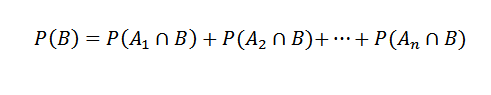
Potom aplikovanie vety o násobení
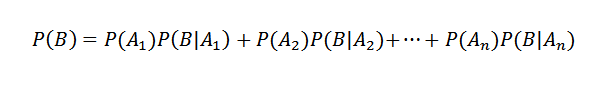
Na druhej strane je podmienená pravdepodobnosť AI B definovaná
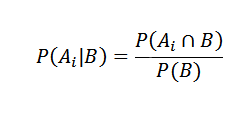
Správne nahradenie, máme to pre každého i
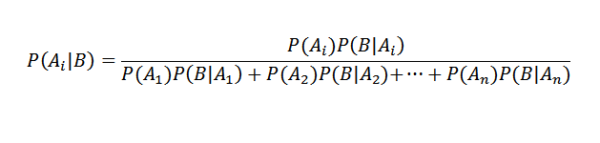
Aplikácie Bayesovej vety
Vďaka tomuto výsledku sa výskumným skupinám a rôznym korporáciám podarilo zlepšiť systémy, ktoré sú založené na znalostiach.
Štúdia choroby
Napríklad pri štúdiu chorôb môže Bayesova veta pomôcť rozlíšiť pravdepodobnosť, že choroba sa nachádza v skupine ľudí s danou charakteristikou, pričom ako údaje berú globálne miery choroby a prevaha uvedených charakteristík v oboch Zdraví a chorá ľudia.
Vývoj softvéru
Na druhej strane vo svete vysokých technológií ovplyvnila veľké spoločnosti, ktoré vďaka tomuto výsledku vyvinuli softvér „na základe znalostí“.
Ako denný príklad máme asistenta kancelárie Microsoft Office. Bayesova veta pomáha softvéru vyhodnotiť problémy, ktoré užívateľ predstavuje, a určiť, aké rady poskytne, a tak byť schopný ponúknuť lepšiu službu podľa zvykov používateľa.
Je potrebné poznamenať, že tento vzorec bol ignorovaný až do nedávnej doby, je to hlavne preto, že keď bol tento výsledok vyvinutý pred 200 rokmi, pre nich bolo malé praktické využitie. V našej dobe však vedci vďaka veľkému technologickému pokroku dosiahli spôsoby, ako tento výsledok do praxe.
Vyriešené cvičenia
Cvičenie 1
Spoločnosť mobilných telefónov má dva stroje A a B. 54% mobilných telefónov vyrába stroj A a zvyšok podľa stroja B. Nie všetky mobilné telefóny sú v dobrom stave.
Môže vám slúžiť: faktorizáciaPodiel defektných mobilných telefónov vyrobených A je 0.2 a pre B je 0.5. Aká je pravdepodobnosť, že mobilný telefón uvedeného továrne je chybný? Aká je pravdepodobnosť, že s vedomím, že mobilný telefón je chybný, pochádza zo stroja do?
Riešenie
Tu máte experiment, ktorý sa vykonáva v dvoch častiach; V prvej časti sa udalosti vyskytujú:
TO: Mobilný telefón vyrobený strojom a.
B: Mobilný telefón vyrobený strojom B.
Pretože stroj A produkuje 54% mobilných telefónov a zvyšok sa vyrába strojom B, stroj B musí produkovať 46% mobilných telefónov. Je uvedená šanca na tieto udalosti, a to:
P (a) = 0,54.
P (b) = 0,46.
Udalosti druhej časti experimentu sú:
D: Defektný mobilný telefón.
E: nedefektívna bunka.
Ako je uvedené vo vyhlásení, pravdepodobnosť týchto udalostí závisí od výsledku získaného v prvej časti:
P (d | a) = 0,2.
P (d | b) = 0,5.
Pomocou týchto hodnôt môžete tiež určiť pravdepodobnosti príslušenstva týchto udalostí, to znamená:
P (e | a) = 1 - p (d | a)
= 1 - 0,2
= 0,8
a
P (e | b) = 1 - p (d | b)
= 1 - 0,5
= 0,5.
Teraz je možné udalosť D napísať takto:
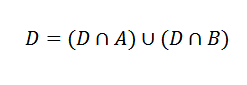 Tieto udalosti sa vzájomne vylučujú.
Tieto udalosti sa vzájomne vylučujú.
Použitím vety násobenia pre podmienenú pravdepodobnosť je:
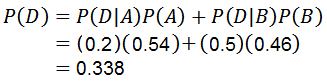
Na ktorú je zodpovedaná prvá otázka.
Teraz potrebujeme iba vypočítať p (a | d), pre ktorú sa aplikuje Bayesova veta:
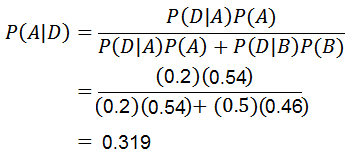
Vďaka Bayesovej vete možno potvrdiť, že pravdepodobnosť, že mobilný telefón bol vyrobený strojom A, s vedomím, že mobilný telefón je chybný, je 0.319.
Môže vám slúžiť: IcosagonoCvičenie 2
Tri škatule obsahujú čierne a čierne gule. Zloženie každého z nich je nasledujúce: u1 = 3b, 1n, u2 = 2b, 2n, u3 = 1b, 3n.
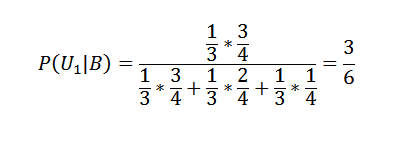
Náhodne zvolený jeden z krabíc a náhodná guľa sa z nej extrahuje, ktorá sa ukáže ako biela. Čo je krabica s najpravdepodobnejšími zvolenými?
Riešenie
Prostredníctvom U1, U2 a U3 budeme tiež predstavovať vybranú krabicu.
Tieto udalosti tvoria oddiel S a overuje sa, že p (u1) = p (u2) = p (u3) = 1/3, pretože výber poľa je náhodný.
Ak b = extrahovaná guľa je biela, budeme mať p (b | u1) = 3/4, p (b | u2) = 2/4, p (b | u3) = 1/4 .
Čo chceme získať, je pravdepodobnosť, že lopta bola prevzatá z krabice IU s vedomím, že táto lopta bola biela, tj P (ui | b) a zistenie, ktorá z týchto troch hodnôt bola najvyššia z toho krabica s väčšou pravdepodobnosťou extrakcia bielej gule.
Aplikácia Bayesovej vety na prvé z políčok:
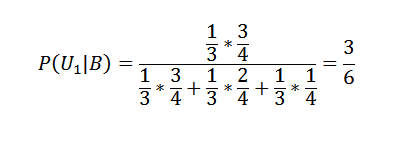
A pre ďalšie dve:
P (u2 | b) = 2/6 a p (u3 | b) = 1/6.
Potom je prvá z krabíc, ktorá má väčšiu pravdepodobnosť, že bude vybraná na extrakciu bielej gule.