Teória charakteristík súborov, prvky, príklady, cvičenia

Ten teória Je to odvetvie logickej matematiky, ktorá je zodpovedná za štúdium vzťahov medzi entitami nazývané súpravy. Sady sa vyznačujú tým, že sú zbierky predmetov rovnakej povahy. Tieto objekty sú prvkami množiny a môžu byť: čísla, písmená, geometrické obrázky, slová, ktoré predstavujú objekty, samotné objekty a ďalšie.

Bol to Georg Cantor, ku koncu 19. storočia, ktorý navrhol súbor sád. Zatiaľ čo iní významní matematici v dvadsiatom storočí urobili svoju formalizáciu: Gottlob Frege, Ernst Zermelo, Bertrand Russell, Adolf Fraenkel.

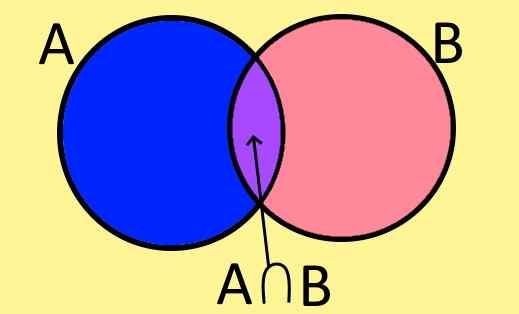
postava 1. Venn Diagram sadov A, B a ich križovatka A⋂ B. (Vlastné rozpracovanie).

Vennové diagramy sú grafickým spôsobom, ako reprezentovať súbor, a pozostáva z uzavretej plochej postavy, v ktorej sú prvky sady.

Napríklad obrázok 1 zobrazuje dve sady A a B, ktoré majú spoločné prvky, prvky spoločné pre A a B. Tieto tvoria novú sadu nazývanú križovatka A a B, ktorá je napísaná symbolicky takto:

A ∩ B

[TOC]

Charakteristika

Sada je primitívny koncept, ako je v geometrii koncept bodu, rovného alebo plochého. Neexistuje lepší spôsob, ako vyjadriť tento koncept, ako poukázať na príklady: 

Sada a tvorená farbami španielskej vlajky. Tento spôsob vyjadrenia súboru sa nazýva porozumením. Rovnaká sada a napísaná rozšírením je:

E = červená, žltá

V tomto prípade sú červené a žlté prvky súpravy a. Je potrebné poznamenať, že prvky sú uvedené medzi kľúčmi a neopakujú sa. V prípade španielskej vlajky sú tri pruhy farieb (červená, žltá, červená), z ktorých dva sa opakujú, ale prvky sa neopakujú, keď je sada vyjadrená.

Predpokladajme Set V Formované prvými tromi vokálnymi písmenami:

V = a, e, i

Sila V, ktorá je označená p (v), je sada všetkých súborov, ktoré je možné vytvoriť s prvkami V:

P (v) = a, e, i, a, e, a, i, e, i, a, e, i

Typy súborov

Konečná súprava

Je to sada, v ktorej sú jeho prvky počítanie. Príkladmi konečných súborov sú listy španielskej abecedy, samohlásky španielčiny, planéty slnečnej sústavy. Počet prvkov konečnej sady sa nazýva jej kardinalita.

Nekonečná súprava

Infinite Ensemble, každý, kto je počet svojich prvkov, je nesúvislý, pretože bez ohľadu na to, aký veľký je počet jeho prvkov, je vždy možné nájsť viac prvkov.

Nekonečným nastaveným príkladom je sada prírodných čísel n, ktoré sa vo veľkej miere vyjadrujú nasledovne:

Môže vám slúžiť: Coplanares body: rovnica, príklad a vyriešené cvičenia

N = 1, 2, 3, 4, 5, .. . je jednoznačne nekonečná súprava, pretože nezáleží na tom, aké veľké môže byť prirodzené číslo, nasledujúci major môže vždy nájsť v nekonečnom procese. Je zrejmé, že kardinalita nekonečnej sady je ∞.

Prázdna súprava

Je to sada, ktorá neobsahuje žiadny prvok. Prázdna súprava V je označená Ø alebo pomocou kľúča bez prvkov vo vnútri:

V = = Ø.

Prázdna súprava je jedinečná, preto musí byť nesprávna povedať „prázdna súprava“, správnym formulárom je povedať „prázdna sada“.

Medzi vlastnosťami prázdnej sady je to, že je to podskupina akejkoľvek množiny:

Ø ⊂ a

Okrem toho, ak je sada podmnožinou prázdnej sady, potom bude táto sada nevyhnutne prázdnota:

A ⊂ Ø ⇔ a = Ø

Jednotka

Nazýva sa Unitary Set Afecl Shot, ktorá obsahuje jeden prvok. Napríklad súbor prírodných satelitov Zeme je jednotková súprava, ktorej jediným prvkom je mesiac. Nastavte B celých čísel menších ako 2 a viac ako nula má iba prvok 1, preto je to jednotka.

Binárna súprava

Sada je binárna, ak má iba dva prvky. Napríklad nastavte x, takže x je skutočný počet x^2 = 2 = 2. Táto sada rozšírenia je napísaná takto:

X = -√2, +√2

Univerzálny súbor

Univerzálna sada je sada, ktorá obsahuje ďalšie sady rovnakého typu alebo prírody. Napríklad univerzálna sada prírodných čísel je sada reálnych čísel. Reálne čísla sú však tiež univerzálne z celých čísel a racionálnych čísel.

Základné položky

- Vzťahy medzi súbormi

V súprave môžete nadviazať niekoľko typov vzťahov medzi nimi a ich prvkami. Ak majú dve sady A a B presne rovnaké prvky, medzi nimi je rovnaký vzťah označený takto:

Do = B

Ak všetky prvky súboru patria do súboru B, ale nie všetky prvky B patria do A, potom medzi nimi existuje vzťah zaradenia, ktorý je označený takto:

A ⊂ B, ale b ⊄ a

Predchádzajúci výraz znie: A je podmnožina B, ale B nie je podmnožinou a.

Na označenie toho, že niektoré alebo niektoré prvky patria do súboru, sa používa symbol príslušnosti ∈ napríklad, aby povedal, že prvok X alebo prvky patria do množiny A, je napísané symbolicky takto:

x ∈ A

Áno, prvok a nepatrí do súboru tohto vzťahu, je napísané takto:

a ∉ a

Spolupracujúci vzťah je uvedený medzi prvkami množiny a sadou, s výnimkou výnimky sily výkonu, pričom súprava je zbierka alebo sada všetkých možných množín, ktoré je možné formovať prvkami uvedenej sady.

Môže vám slúžiť: faktorizácia

Predpokladajme v = a, e, i, tvoja sila je p (v) = a, e, i, a, e, a, i, e, i, a, e, i, v takom prípade sa sada V stáva prvkom množiny p (v) a dá sa napísať:

V ∈ P (v)

- Inklúzne vlastnosti

Prvá vlastnosť začlenenia ustanovuje, že každá sada je obsiahnutá sama osebe alebo inými slovami, čo je samo osebe podskupinou:

⊂ a

Ďalšou vlastnosťou zaradenia je tranzitivita: ak je podmnožina B a B, je to podskupina C, potom A je podmnožina C. Symbolly je vzťah tranzitivity napísaný takto:

(A ⊂ b) ^ (b ⊂ c) => a ⊂ c

Nižšie je Diagram Venn, ktorý zodpovedá tranzitivite inklúzie:

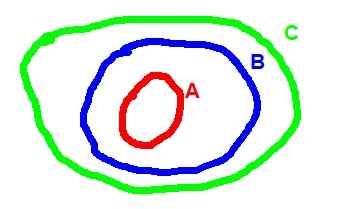Obrázok 2. (A ⊂ b) ^ (b ⊂ c) => a ⊂ c

- Operácie medzi sadami

Križovatka

Križovatka je operácia medzi dvoma súbormi, ktorá vedie k novej sade patriace do tej istej univerzálnej sady prvých dvoch. V tomto zmysle je to uzavretá operácia.

Symbolicky je operácia križovatky formulovaná takto:

A⋂b = x / x∈A ^ x∈B

Príkladom je nasledujúci: Nastavte písmená slova „prvky“ a nastavte B písmen slova „opakované“, križovatka medzi A a B je napísaná takto:

A⋂b = e, l, m, n, t, s ⋂ r, e, p, t, i, d, o, s = e, t, s . Univerzálna sada A, z B a tiež A⋂B je súbor písmen španielskej abecedy.

Zväzok

Únia dvoch sád je sada tvorená prvkami spoločnými pre dve sady a non -common prvky týchto dvoch sád. Operácia Únie medzi súbormi je vyjadrená symbolicky takto:

A∪b = x/x∈A v x∈B

Rozdiel

Prevádzka súpravy aspoň súbor označuje A-B. A-B je nová sada tvorená všetkými prvkami, ktoré sú v a, ktoré nepatria k B. Symbol je napísaný takto:

A - b = x/ x ∈ A ^ x ∉ b

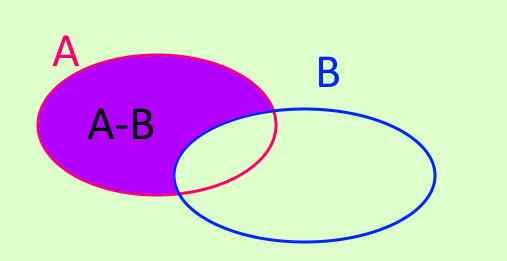Obrázok 3. A - b = x/ x ∈ A ^ x ∉ b

Symetrický rozdiel

Symetrický rozdiel je operácia medzi dvoma množinami, kde výsledná súprava je tvorená prvkami, ktoré nie sú spoločné pre tieto dve sady. Symetrický rozdiel je symbolicky reprezentovaný takto:

A⊕b = x/ x∈ (a-b) ^ x∈ (b-a)

Príklady

Príklad 1

Vennový diagram je grafický spôsob, ako reprezentovať sady. Napríklad nastavenie C písmen sada slova je znázornená takto:

Príklad 2

Je uvedené nižšie cez Venn Diagrams, že sada samohlások v slove „set“ je podmnožinou množiny písmen slova „set“.

Môže vám slúžiť: vzorkovanie kvót: Metóda, výhody, nevýhody, príklady

Príklad 3

Súbor Ñ Z písmen španielskej abecedy je to konečná súprava, táto sada podľa rozšírenia je napísaná takto:

Ñ = A, B, C, D, E, F, G, H, I, J, K, L, M, N, O, O, P, Q, R, S, T, U, V, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, x, y, z a jeho kardinalita je 27.

Príklad 4

Súbor Vložka Z samohlások v španielčine je to podskupina sady ñ:

Vložka ⊂ Ñ Preto je to konečná súprava.

Konečná súprava Vložka Rozšírený spôsob, ako je napísaný takto: Vložka = a, e, i, o, u a jej kardinalita je 5.

Príklad 5

Vzhľadom na súpravy a = 2, 4, 6, 8 a b = 1, 2, 4, 7, 9 Určte a-b a b-a b-a. 

A - B sú prvky, ktorých nie sú v B:

A - b = 6, 8

B - A sú prvky B, ktoré nie sú v:

B - a = 1, 7, 9

Vyriešené cvičenia

Cvičenie 1

Symbolicko a tiež rozšíriť okvetné lístky prírodných čísel ešte nižšie ako 10.

Riešenie: P = x∈ N / x < 10 ^ x mod 2 = 0

P = 2, 4, 6, 8

Cvičenie 2

Predpokladajme, že celok tvoria prírodné čísla, ktoré sú faktormi 210, a množina B tvorená bratrancami prírodných čísel nižších ako 9. Určte obe sady podľa rozšírenia a zistite, aký vzťah existuje medzi týmito dvoma súbormi.

Riešenie: Na určenie prvkov set a musíte začať nájdením faktorov prírodného čísla 210:

210 = 2 * 3 * 5 * 7

Potom nastaviť A je napísané:

A = 2, 3, 5, 7

Pokračujeme v zvažovaní súboru B, čo sú bratranci menšie ako 9. 1 nie je bratranec, pretože nespĺňa definíciu bratranca: „Číslo je bratranec, ak a iba vtedy, ak má presne dva deliteľy 1 a samotné číslo“. 2 je párne a zároveň je bratranec, pretože spĺňa definíciu bratranca, ostatní bratranci menší ako 9 sú 3, 5 a 7. Takže táto sada B je:

B = 2, 3, 5, 7

Preto sú tieto dve sady rovnaké: a = B.

Cvičenie 3

Určiť sadu, ktorej prvky x sa líšia od x.

Riešenie: C = x / x ≠ x

Rovnako ako akýkoľvek prvok, číslo alebo objekt sa rovnajú samotnému, je nastavená C nemôže byť iná ako prázdna sada:

C = Ø

Cvičenie 4

Byť set n prírodných čísel a z množiny celých čísel. Stanovte n ⋂ z y n ∪ z.

Riešenie: 

N ⋂ z = x ∈ Z / x ≤ 0 = (-∞, 0]

N ∪ z = z Pretože n ⊂ z.

Odkazy

1. Garo, m. (2014). Matematika: Kvadratické rovnice: Ako vyrieši kvadratickú rovnicu. Marilù garo.
2. Haeussler, e. F., & Paul, r. Siež. (2003). Matematika pre správu a ekonomiku. Pearson Vzdelanie.
3. Jiménez, J., Rodríguez, m., Estrada, r. (2005). Matematika 1 september. Prah.
4. Vzácny, c. Tón. (2005). Kurz matematiky 3o. Redakčný progreso.
5. Matematika 10 (2018). „Príklady konečných súborov“. Zdroj: Mathematics10.slepo
6. Wikipedia. Teória. Obnovené z: je.Wikipedia.com