Teleskopické leto, ako sa vyrieši a vyriešené cvičenia

Ten zhrnutie Teleskopický Je to pobočka operácií s číselnou sériou. Rieši súhrny prvkov od počiatočnej hodnoty po „n“ výrazov, ktorých argument je spôsobený ktorýmkoľvek z nasledujúcich vzorov:

(F_X - F_x+1); F_x+1  - F_X)

Kde je jeho súhrnný výraz definovaný takto: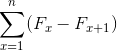

Tiež:

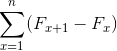
Zdroj: Pixabay.com

Predstavujú sumu prvkov, ktoré pri vývoji podliehajú zrušeniu opačných podmienok. Spôsobenie nasledujúcej rovnosti pre teleskopické súčty:

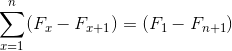
Jeho názov pochádza zo vzťahu so vzhľadom klasického ďalekohľadu, ktorý by sa dal zložiť a nasadiť, čo výrazne zmení jeho rozmer. Podobne sa dajú zhrnúť teleskopické súčty, ktoré sú vo svojej povahe nekonečné, zhrnuté v zjednodušenom výraze:

F₁ - F_N+1

[TOC]

Demonštrácia

Pri vývoji súčtu pojmov je odstránenie faktorov celkom zrejmé. Kde pre každý z prípadov sa v nasledujúcom iterácii objavia opačné prvky.

Prvý prípad sa bude brať ako príklad (f_X - F_x+1), pretože tento proces funguje homológne s (f_x+1-F_X).

Vypracovanie prvých 3 hodnôt 1, 2, 3 Je pozorovaná tendencia zjednodušenia

X₁     (F₁ - F₁₊₁) = F₁ - F₂

X₂     (F₂ - F₂₊₁) = F₂ - F₃

X₃     (F₃ - F₃₊₁) = F₃ - F₄

Kde vyjadrením súčtu opísaných prvkov:

X₁ + X₂ + X₃ = F₁ - F₂ + F₂ - F₃ + F₃ - F₄

Zistilo sa, že výrazy f₂ a f₃ Sú opísané svojimi protikladmi, vďaka ktorým je ich zjednodušenie nevyhnutné. Rovnakým spôsobom sa zistí, že výrazy f₁ a f₄ zostať.

Ak bola suma vyrobená z x = 1 do x = 3, znamená to, že prvok f₄ zodpovedá všeobecnému termínu f_N+1.

Tým demonštruje rovnosť:

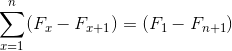
Ako sa vyrieši?

Účelom teleskopických súčtov je uľahčiť prácu, takže nie je potrebné rozvíjať nekonečné množstvo výrazov alebo zjednodušiť príliš dlhý reťazec.

Môže vám slúžiť: Trachtenberg Metóda: Čo je to, príklady

Na rozlíšenie bude potrebné iba vyhodnotiť podmienky f₁ a f_N+1. Tieto jednoduché substitúcie tvoria konečný výsledok sumy.

Celkom pojmov sa nebude vyjadriť, čo sa stane potrebným na demonštráciu výsledku, ale nie pre normálny proces výpočtu.

Dôležitá vec je všimnúť si konvergenciu numerickej série. Niekedy sa argument sumy nebude vyjadriť teleskopickým spôsobom. V týchto prípadoch je vykonávanie metód alternatívnej faktorizácie veľmi bežné.

Charakteristická metóda faktorizácie v teleskopických súhrnoch je metóda jednoduchých frakcií. K tomu dochádza, keď sa pôvodný frakčný rozkladá na súčet niekoľkých frakcií, kde je možné pozorovať teleskopický vzor (F (F_X - F_x+1) alebo (f_x+1  - F_X).

Rozklad v jednoduchých zlomkoch

Na overenie konvergencie numerických sérií je veľmi bežné transformovať racionálne výrazy pomocou metódy jednoduchých frakcií. Cieľom je modelovať argument až do formy teleskopického súčtu.

Napríklad nasledujúca rovnosť predstavuje rozklad v jednoduchých frakciách:

Pri vývoji numerickej série a uplatňovaní zodpovedajúcich vlastností má výraz takto:

Kde je viditeľná teleskopická forma (f_X - F_x+1).

Postup je dosť intuitívny a spočíva v nájdení hodnôt čitateľa, ktoré bez porušenia rovnosti umožňujú oddelenie produktov, ktoré sú v menovateľovi. Rovnice, ktoré vznikajú pri určovaní týchto hodnôt, sa zvyšujú podľa porovnania medzi oboma stranami rovnosti.

Tento postup sa pozoruje krok za krokom pri vývoji cvičenia 2.

Môže vám slúžiť: 6 zábava matematické hádanky pre deti

História

Je celkom neisté byť schopný definovať historický moment, v ktorom boli prezentované teleskopické súčty. Jeho implementácia sa však začína vidieť v sedemnástom storočí, v číselných sériových štúdiách, ktoré uskutočnili Leibniz a Huygens.

Obaja matematici pri skúmaní súčtov trojuholníkových čísel si začínajú všímať trendy v zbližovaní určitých sérií nasledujúcich prvkov. Ale ešte zaujímavejšie je začiatok modelovania týchto výrazov, v prvkoch, ktoré sa nemusia nevyhnutne stať.

V skutočnosti výraz, ktorý sa predtým používal na označenie jednoduchých frakcií:

Predložil ho Huygens a okamžite sa nazýva Leibnizova pozornosť. Ktorí v priebehu času mohli pozorovať konvergenciu na hodnotu 2. Bez toho, aby to vedel, implementoval teleskopické zhrnutie.

Cvičenia

Cvičenie 1

Definujte, ktorý termín konvertuje nasledujúca suma:

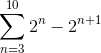
Ak sa suma rozvíja manuálne, pozoruje sa nasledujúci vzor:

(2³ - 2⁴) + (2⁴ - 2⁵) + (2⁵ - 2⁶)… (2¹⁰ - 2^jedenásť)

Kde faktory od 2⁴ Až 2¹⁰ Predstavujú pozitívne a negatívne časti, čím sa ich zrušenie prejavuje. Potom jediné faktory, ktoré sa nezjednodušia, budú prvé „2³"A posledný" 2^jedenásť„.

Týmto spôsobom sa pri implementácii teleskopických súhrnných kritérií získa:

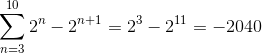
Cvičenie 2

Transformujte argument na teleskopický súčet typu a definujte konvergenciu série:

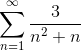
Ako je uvedené vo vyhlásení, prvá vec bude rozložiť sa v jednoduchých frakciách, aby sa prehodnotil argument a vyjadril ho v teleskopickej podobe.

2 frakcie, ktorých menovatelia sú „n“ a „n+1“, musia sa nájsť, ak použitá metóda nižšie musí dosiahnuť hodnoty čitateľa, ktorý spĺňa rovnosť.

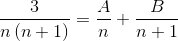
Hodnoty A a B sú definované. Vytvára sa prvá suma zlomkov.

Môže vám slúžiť: 60 deliteľov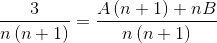

Potom sú menovatelia zjednodušili a vytvorí sa lineárna rovnica.

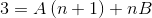
V ďalšom kroku je expresia pravej strany prevádzkovaná, až kým sa porovnáva vzor s „3“ vľavo.

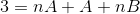
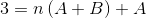
Na definovanie rovníc, ktoré sa majú použiť, sa musia porovnať výsledky oboch strán rovnosti. To znamená, že na ľavej strane sa nepozorujú žiadne premenné n hodnoty, týmto spôsobom sa musí A +B rovnať nule.

A + b = 0; A = -b

Na druhej strane, konštantná hodnota sa bude musieť rovnať konštantnej hodnote 3.

A = 3

Preto.

A = 3 a b = -3

Už definované hodnoty čitateľa pre jednoduché frakcie, suma je prehodnotenie.

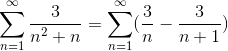
Kde sa už dosiahla generická forma teleskopického súčtu. Teleskopická séria je vyvinutá.

Kde vydelením veľmi veľkého počtu sa výsledok približuje čoraz viac a pozoruje konvergenciu série na hodnotu 3.

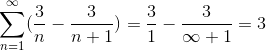
Tento typ série sa nemohol vyriešiť inými slovami, kvôli nekonečnému množstvu iterácií, ktoré problém definujú. Táto metóda však spolu s mnohými ďalšími zarámuje odvetvie štúdia numerickej série, ktorej cieľom je určiť hodnoty konvergencie alebo definovať divergenciu týchto sérií.

Odkazy

1. Lekcie nekonečného výpočtu. Manuel Franco, Manuel Franco Nicolás, Francisco Martínez González, Roque Molina Legaz. Editum, 1994.
2. Komplexný výpočet: úspechy a séria funkcií. Antonio Rivera Figueroa. Redakčná skupina Patria, 21. októbra. 2014.
3. Kurz v počte a skutočná analýza. Sudhir r. GhorPade, Balmohan V. Limit. Springer Science & Business Media, 5. júna. 2006.
4. Nekonečné série. Tomlinson Fort. The Clarendon Press, 1930.
5. Prvky teórie nekonečných sprievodov. Lloyd Leroy Smail. McGraw-Hill Book Company, Incorpan, 1923.