Príklady kvadratických úspechov, pravidlá a cvičenia vyriešené

Ten Kvadratické úspechy, Z matematického hľadiska pozostávajú zo sekvencií čísel, ktoré sledujú určité aritmetické pravidlo. Je zaujímavé poznať toto pravidlo, aby ste určili ktorékoľvek z podmienok nástupníctva.

Jedným zo spôsobov, ako to dosiahnuť, je určiť rozdiel medzi dvoma po sebe nasledujúcimi výrazmi a zistiť, či sa získaná hodnota vždy opakuje. Keď áno, hovorí sa, že je to pravidelný postup.

Numerické scény sú spôsob, ako organizovať sekvencie čísel. Zdroj: Pixabay.com

Ale ak sa neopakuje, môžete skúsiť preskúmať Rozdiel medzi rozdielmi A zistite, či je táto hodnota konštantná. Ak áno, potom je to Kvadratická sukcesia. 

[TOC]

Príklady pravidelných úspechov a kvadratických úspechov

Nasledujúce príklady pomáhajú objasniť, čo bolo doteraz vysvetlené:

Príklad pravidelnej sukcesie

Byť sukcesia s = 4, 7, 10, 13, 16, ...

Táto sukcesia, označovaná S, je nekonečná numerická súprava v tomto prípade celých čísel.

Je zrejmé, že ide o pravidelnú sukcesiu, pretože každý výraz sa získa pridaním 3 do predchádzajúceho termínu alebo prvku:

4

4 +3 = 7

7+3 = 10

10+3 = 13

13+3 = 16

Inými slovami: Táto sukcesia je pravidelná, pretože rozdiel medzi nasledujúcim pojmom a predchádzajúcom dáva pevnú hodnotu. V príklade vzhľadom na túto hodnotu je 3.

Pravidelné úspechy získané pridaním pevnej sumy do predchádzajúceho funkčného obdobia sa tiež nazývajú aritmetické progresie. A na rozdiel - konštantný - medzi následnými výrazmi, ktoré sa nazýva dôvod A je označený ako r.

Príklad neregistrovanej a kvadratickej sukcesie

Pozrite si teraz nasledujúcu sukcesiu:

S = 2, 6, 12, 20, 30, .. .

Keď sa vypočítajú následné rozdiely, získajú sa nasledujúce hodnoty:

Môže vám slúžiť: náhodné výbery s výmenou alebo bez výmeny

6-2 = 4

12-6 = 6

20-12 = 8

30-20 = 10

Ich rozdiely nie sú konštantné, takže sa dá povedať, že ide o neregistrovanú sukcesiu.

Ak však uvažujeme o súbore rozdielov, existuje ďalšia sukcesia, ktorá bude označená ako S_Rozmach:

Siež_Rozmach = 4, 6, 8, 10, .. .

Táto nová sukcesia je a pravidelný postup, Pretože každý termín sa získa pridaním pevnej hodnoty r = 2 k predchádzajúcej. Preto môžeme potvrdiť, že S je Kvadratická sukcesia.

Všeobecné pravidlo na vybudovanie kvadratickej sukcesie

Existuje všeobecný vzorec na vybudovanie kvadratickej sukcesie:

Tón_n = A ∙ n² + B ∙ n +c

V tomto vzorci, t_n Je to termín n sukcesie. A, B a C sú pevné hodnoty, zatiaľ čo n sa mení jeden po druhom, to je 1, 2, 3, 4, ..

Postupne v predchádzajúcom príklade a = 1, b = 1 a c = 0. Odtiaľ z toho vyplýva, že vzorec, ktorý generuje všetky výrazy, je: t_n = n² + n

To znamená:

Tón₁ = 1² + 1 = 2

Tón₂ = 2² + 2 = 6

Tón₃ = 3² + 3 = 12

Tón₅ = 5² + 5 = 30

Tón_n = n² + n

Rozdiel medzi dvoma po sebe idúcimi podmienkami kvadratického dedenia

Tón_N+1 - Tón_n = [A ∙ (n+1)² + B ∙ (n + 1) + c] - [a ∙ n² + B ∙ n +c]

Vývoj výrazu prostredníctvom pozoruhodného produktu zostáva:

Tón_N+1 - Tón_n = A ∙ n² + A ∙ 2 ∙ n + a + b ∙ n + b + c - a ∙ n² - B ∙ n - c

Zjednodušením dostanete:

Tón_N+1 - Tón_n = 2 ∙ a ∙ n + a + b

Toto je vzorec, ktorý dáva postupnosť rozdielov s_Rozmach To je možné napísať takto:

Rozmach_n = A ∙ (2n+1)+b

Kde je zrejmé, že nasledujúci termín je 2 ∙ niekedy predchádzajúci. To znamená dôvod sukcesie rozdielov s_Rozmach Es: r = 2 ∙ a.

Vyriešené cvičenia kvadratických úspechov

Cvičenie 1

Byť sukcesia s = 1, 3, 7, 13, 21,…. Určite áno:

i) Je to pravidelné alebo nie

ii) je kvadratický alebo nie

iii) bol kvadratický, postupnosť rozdielov a ich dôvod

Môže vám slúžiť: obmedzte vlastnosti (s príkladmi)

Odpovedať

i) Vypočítajme rozdiel nasledujúci pojem a predchádzajúci: predchádzajúci:

3-1 = 2

7-3 = 4

13-7 = 6

21-13 = 8

Môžeme potvrdiť, že dedičstvo nie je pravidelné, pretože rozdiel medzi postupnými pojmami nie je konštantný.

ii) Postupnosť rozdielov je pravidelná, pretože rozdiel medzi jeho výrazmi je konštantná hodnota 2. Preto je pôvodná sukcesia kvadratická.

iii) Už sme určili, že S je kvadratický, postupnosť rozdielov je:

Siež_Rozmach = 2, 4, 6, 8,… a jeho dôvod je r = 2.

Cvičenie 2

Byť sukcesia s = 1, 3, 7, 13, 21,… predchádzajúceho príkladu, kde sa overilo, že je kvadratický. Určiť:

i) vzorec, ktorý určuje všeobecný termín t_{n .}

ii) Overte tretí a piaty termín.

iii) hodnota desiateho termínu.

Odpovedať

i) všeobecný vzorec T_n je ∙ n² + B ∙ n +c. Potom je známe hodnoty a, b a c.

Postupnosť rozdielov je správna 2. Okrem akéhokoľvek kvadratického dedenia je dôvod r je 2 ∙ a, ako je uvedené v predchádzajúcich oddieloch.

R = 2 ∙ a = 2, čo nás vedie k záveru, že a = 1.

Prvé funkčné obdobie sukcesie rozdielov s_Rozmach Je 2 a musí dodržiavať pri ∙ (2n+1)+b, s n = 1 a a = 1, to znamená:

2 = 1 ∙ (2 ∙ 1+1)+b

Získava sa B = -1

Potom prvý termín S (n = 1) Vale 1, to znamená: 1 = a ∙ 1² + B ∙ 1 + C. Ako už vieme, že a = 1 a b = -1, nahradenie nás, zostávame:

1 = 1 ∙ 1² + (-1) ∙ 1 +c

Vymazanie C sa získa jeho hodnota: C = 1.

Súhrn:

A = 1, b = -1 a c = 1

Potom je tento termín spravodlivý_n = n² - N + 1

ii) Tretie funkčné obdobie t₃ = 3² - 3 + 1 = 7 a je overený. Piaty t₅ = 5² - 5 + 1 = 21, ktoré je tiež overené.

iii) desiaty termín bude T₁₀ = 10² - 10 + 1 = 91.

Cvičenie 3

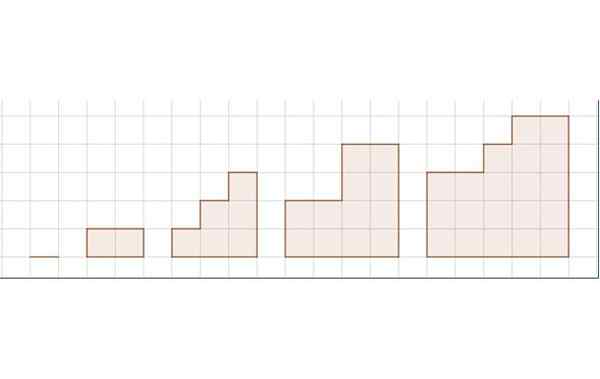Sekvencia oblastí pre cvičenie 3. Zdroj: Self Made.

Obrázok ukazuje sekvenciu piatich obrázkov. Návod predstavuje jednotku dĺžky.

Môže vám slúžiť: rozdiel medzi spoločnou frakciou a desatinným číslom

i) Stanovte dedičstvo pre oblasť čísel.

i) ukážte, že je to kvadratická sukcesia.

iii) Nájdite plochu na obrázku č. 10 (nie je zobrazené).

Odpovedať

i) Postupnosť zodpovedajúca oblasti postupnosti obrázkov je:

S = 0, 2, 6, 12, 20,…

ii) Postupnosť zodpovedajúca po sebe nasledujúcim rozdielom podmienok S je:

Siež_Rozmach = 2, 4, 6, 8,…

Pretože rozdiely medzi po sebe idúcimi výrazmi nie sú konštantné, takže S nie je pravidelná sukcesia. Musí vedieť, či je kvadratický, pre ktoré opäť robíme sekvenciu rozdielov a získame:

2, 2, 2, .. .

Pretože sa opakujú všetky výrazy sekvencie, potvrdzuje sa, že S je kvadratická sukcesia.

iii) dedičstvo s_Rozmach je pravidelný a jeho dôvod R je 2. Použitím predtým demonštrovanej rovnice r = 2 ∙ a zostáva:

2 = 2 ∙ a, čo znamená, že a = 1.

Druhé funkčné obdobie sukcesie rozdielov s_Rozmach Je to 4 a n-eme of s_Rozmach je

A ∙ (2n+1)+B.

Druhý termín má n = 2. Tiež sa zistilo, že a = 1, takže pomocou predchádzajúcej rovnice a jej výmenu je:

4 = 1 ∙ (2 ∙ 2+1)+b

Získava sa B = -1.

Je známe, že druhé funkčné obdobie S má hodnotu 2 a že vzorec všeobecného pojmu sa musí splniť s n = 2:

Tón_n = A ∙ n² + B ∙ N +C; n = 2; A = 1; B = -1; Tón₂ = 2

To znamená

2 = 1 ∙ 2² - 1 ∙ 2 + c

Dospelo sa k záveru, že C = 0, to znamená, že vzorec, ktorý dáva všeobecný termín sukcesie, je:

Tón_n = 1 ∙ n² - 1 ∙ n +0 = n² - n

Teraz je overený piaty termín:

Tón₅ = 5² - 5 = 20

iii) Obrázok č

Tón₁₀ = 10² - 10 = 90

Odkazy

1. https: // www.Geogebra.orgán