Sú to rektilineálne segmenty, ktoré sú možné v každom mnohouholníku

Diagonál štvorca

Rektilineálne segmenty, ktoré sú možné v každom mnohouholníku, sú diagonála. Diagonál je segment čiary, ktorý je nakreslený spojením dvoch non -adjacentových vrcholov polygónu. Inými slovami, diagonálne čiary začínajú vo vrchole postavy a končia v inom, ktorý nie je ďalej.

Na obrázku vyššie je diagonál štvorca znázornený čiernym zdvihom, ktorý, ako je vidieť, sa spojí s dvoma opačnými rohmi.

Diagonály námestia sa merajú rovnako, ale v kostore sú ich dve uhlopriečky odlišné, je tu väčšia, dlhšia a kratšia, kratšia, kratšia.

Ako vypočítať diagonálne číslo mnohouholníka?

Určenie počtu diagonálov mnohouholníka môže byť jednoduché, pokiaľ ide o štvorcový alebo rhombus, ale ako sa zvyšuje počet strán postavy, je zložitejšie vizualizovať, koľko diagonálov má.

Preto sa v matematike používa jednoduchý vzorec, vďaka ktorému bude tento proces oveľa efektívnejší:

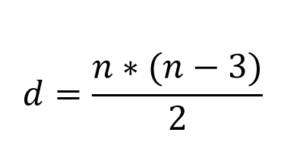
Malo by sa pamätať na to, že n sa rovná počtu strán mnohouholníka a n musí byť vždy väčší ako 3. Pretože? (Pokračujte v čítaní, odpoveď je na konci).

Príklad 1

Vypočítajte množstvo diagonálov osemuholníka.

Octagón je pravidelný osemdesiatylovec, čo znamená, že všetky jeho vnútorné strany a uhly sú rovnaké.

Pomocou predchádzajúceho vzorca stačí nahradiť n osem:

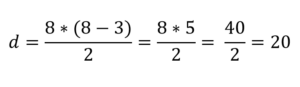
Týmto spôsobom je známe, že počet diagonálov, ktoré sa dajú nakresliť z vrcholov polygónu osemuholníka, je 20.

Môže vám slúžiť: vážené médiá: Ako sa vypočítajú, príklady a cvičenia

Bez vzorca je pravdepodobne ťažkopádne snažiť sa spočítať všetky diagonály, dokonca aj s dobrou kresbou. A čím vyššie je množstvo strán na obrázku, tým zložitejšie bude.

Príklad 2

Vypočítajte dĺžku diagonálu obdĺžnika s vetou Pythagora.

Pythagorasova veta potvrdzuje, že súčet štvorcov kategórií obdĺžnika trojuholníka nazývaný A a B, sa rovná štvorcovi hypotenuse (strana oproti pravému uhlu), nazývaná C.

V algebraickom zápise by to bolo:

do² + b² = c²

Diagonál obdĺžnika vytvára obdĺžnikový trojuholník, ktorý môže použiť túto vetu, kde B je základňa a H je výška.

Ak je základňa 12 cm a výška je 7 cm, pri výmene je:

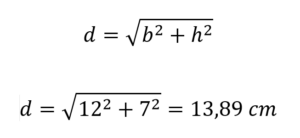
Preto je dĺžka diagonálu uvedeného obdĺžnika 13,89 centimetrov.

Polygón bez diagonálov

Je možné, že existuje polygón, ktorý nemá diagonálne čiary? Ako by to bolo?

Táto hádanka sa dá použiť na výhonok zvedavosti u detí a na to, aby si vizualizovali diagonály postavy:

Triangle je polygón s trom. Ale nemá žiadne diagonály

Áno, trojuholník nemá diagonály.

Vysvetlenie

Triangle je polygón s trom. Ale trojuholníky sú konvexné čísla, ktoré nemajú diagonálne čiary, sú najjednoduchšie a najfascinujúcejšie polygóny matematiky.

Vyzerá dobre na vzorec, ktorý vám umožňuje vypočítať diagonály mnohouholníka:

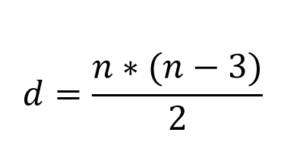
Okamžite sa poznamenáva, že nahradením n = 3 sa získava v dôsledku toho d = 0. To znamená, že trojuholníky nemajú diagonály, neexistuje spôsob, ako nakresliť. Ale napríklad polygóny s n = 4 majú všetky dve diagonály.

Môže vám slúžiť: decagon: pravidelné, nepravidelné, vlastnosti, príklady