Vyriešené aplikácie Fourier Series, príklady a cvičenia

Ten Fourier Series Pozostávajú zo súčtu nekonečných pojmov, ktoré pozostávajú z harmonických funkcií, sínusu a kosínu, ktorých argument je úplne základom základnej frekvencie.

Funkcie sínusu a kosínus sa vynásobia hodnotovými koeficientmi, takže súčet je identický s funkciou T rovnajúcou sa dvojnásobným PI (2π) vydeleným základnou uhlovou frekvenciou Ω Ω Ω Ω Ω Ω Ω Ω Ω Ω Ω Ω Ω.

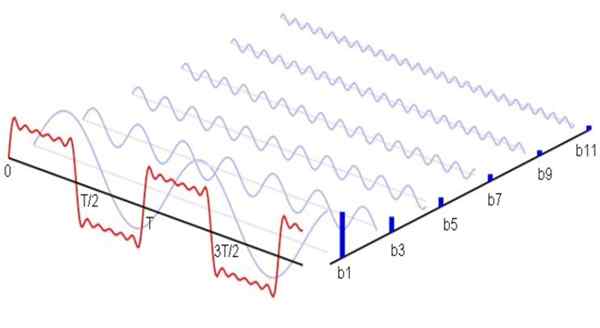
postava 1. Tu je (v modrej) prvá non -nulová harmonika série Fourier, ktorá zodpovedá signálu štvorcového tvaru vlny. Súčet týchto harmonických vedie k červeným signálom. Zdroj: Wikimedia Commons.

Matematicky by to bolo vyjadrené takto: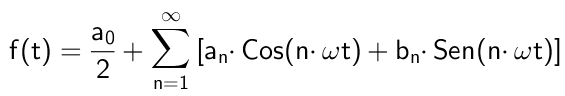

Kde Ω Je to základná frekvencia, ktorá súvisí s obdobím Tón funkcia f (t) Prostredníctvom vzťahu: 

Ω = 2π / t

Za pravidelné obdobie Tón, funkcia f (t) spĺňa túto podmienku:

f (t) = f (t + k t)

Kde klimatizovať Je to celé číslo a koeficienty₀ , do_n a b_n Nazývajú sa Fourierove koeficienty.

[TOC]

Dôležitosť a použitie série Fourier

Názov série Fourier je spôsobený tým, že jeho objaviteľom bol francúzsky matematický.

Tento objav bol základný pre matematiku, pretože ak má diferenciálna rovnica konkrétne harmonické riešenie, potom je možné dosiahnuť všeobecné riešenie pomocou prekrývania alebo súčtu toho istého.

Fourierove koeficienty periodickej funkcie, ktoré sa tiež nazývajú znak, Sú to spektrum toho istého.

Preto spektrom je sada frekvencií, ktoré tvoria signál charakterizovaný amplitúdou každej frekvencie, čo zodpovedá hodnotám Fourierových koeficientov.

Systémy kompresie signálu alebo zvukové a video vlny, vzadu výrazne menší počet bitov ako pôvodný digitalizovaný signál.

Fourierova séria signálu je ako jeho odtlačok prsta v tom zmysle, že, známe koeficienty, ktoré ho tvoria, vždy môžete vedieť, ktoré znamenia patria.

Aj keď použitie série Fourier alebo jej najbežnejšia forma, Fourierovu transformáciu, Ako metóda kompresie signálu je známa už nejaký čas, jeho použitie v praxi muselo čakať na numerické spracovateľy dostatočne rýchle, čo umožnilo stlačenie a dekomprimovanie signálov v „reálnom čase“.

Môže vám slúžiť: štatistické premenné

Príklad série Fourier 

Ďalej príklad funkcie F (T) a jej Fourierovej série.

Funkcia je:

 f (t) = 0 áno 0 ≤ t  < π y 1 si π ≤  t   < 2π

A má zodpovedajúcu sériu Fourier, ktorú dal:

f (t) = ½ - 2/π⋅se (t) - 2/(3π) ⋅se (3T) - 2/(5π) ⋅sen (5T) - 2/(7π) ⋅sen (7T) -…

Nasledujúci obrázok ukazuje funkciu a čiastočné súčty série Fourier:

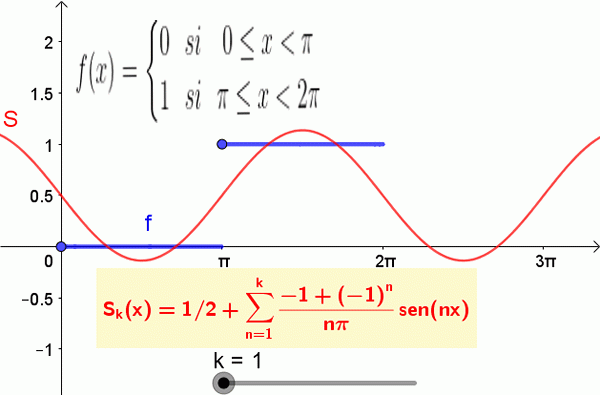Obrázok 2. Zobrazí sa prvých 19 termínov Fourierovej sumy zodpovedajúcej funkcii kroku. Zdroj: f. Zapata.

Stanovenie koeficientov

Nižšie je uvedené, ako určiť Fourierove koeficienty:

Predpokladajme, že funkcia je f (x) definovaná v intervale, ktorý prechádza z t_Jo do t_Jo + T, kde bude kapitál obdobím funkcie. Potom jeho Fourierová séria je:

f (t) = a₀/2 + a₁ cos (Ω t) + a₂ cos (2 Ω t) +… + a_n Cos (n Ω t) +…

.. .+ b₁ sin (Ω t) +b₂ sin (2 Ω t) +… +b_n Hriech (n Ω t) +..

Výpočet nezávislého termínu

Aby sme našli nezávislý pojem, integrujeme oboch členov rovnosti do intervalu definície funkcie:

[t_Jo , tón_Jo+ T]

Preto:

Istota_n ∫cos (n ω t) dt +…

.. .+ b₁ ∫sen (Ω t) dt +b₂ ∫sen (2 Ω t) dt +… +b_n ∫sen (n Ω t) dt +…

Tu symbol ∫ znamená integrál definovaný z T_Jo do t_Jo + Tón.

Integrál prvého funkčného obdobia je T, ktorý pri hodnotení vo výsledkoch hornej hranice:

tón_Jo + Tón

Pri odpočítaní dolnej hranice t_Jo, definitívne t.

Všetky ostatné výrazy sú 0, pretože ide o kosínové alebo sínusové funkcie vyhodnotené v celom období, ako ukazujeme nižšie:

∫cos (nΩ t) dt = (1/ nΩ) ∫cos (nΩ t) d (nΩ t)

Pamätajte, že symbol ∫ znamená integráciu medzi T_Jo do t_Jo + Tón. 

Aby sme urobili integráciu pojmov, ktoré majú kosínus alebo prsník, urobíme nasledujúcu zmenu premennej:

x = Ω (t - t_Jo)

Takže diferenciál x, dx sa rovná diferenciálu d (Ωt).

Takže integrál, ktorý sa má vykonať, je:

Pretože n je celé číslo, potom definovaný integrál vždy dá nulu. To isté platí pre funkciu sínusu.

Preto definovaný integrál vyhodnotený v úplnom období všetkých podmienok obsahuje. 

Môže vám slúžiť: divízie, v ktorých je zvyšok 300

Preto sa dospelo k záveru, že pojem A₀ sa počíta takto:

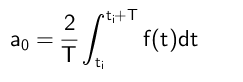
Výpočet koeficientov pre

Na výpočet koeficientov, ktoré sa vynásobia kozínskym funkciám, sa musia vynásobiť obaja členovia rovnosti:

f (t) = a₀/2 + a₁ cos (Ω t) + a₂ cos (2 Ω t) +… + a_n Cos (n Ω t) +…

.. .+ b₁ sin (Ω t) +b₂ sin (2 Ω t) +… +b_n Hriech (n Ω t) +..

Podľa kosínutej funkcie vyhodnotenej v zodpovedajúcom harmonickom a potom sa použije integrál definovaný v celom období obom členom. 

Napríklad na výpočet_m Obaja členovia sa vynásobia cos (MΩt):

f (t) cos (m Ω t) = a₀/2 cos (M Ω t) + a₁ cos (c) cos (M Ω t) + a₂ cos (2 Ω t) cos (M Ω t) +… + do_n Cos (n Ω t) cos (m Ω t) +…

.. .+ b₁ sin (co) cos (m Ω t) +b₂ sin (2 Ω t) cos (m Ω t) +… +b_n Sin (n Ω t) cos (M Ω t) +..

Potom integrujte do úplného obdobia, to znamená v intervale, ktorý prechádza z T_Jo do t_Jo + Tón.

Integrál pojmu obsahujúceho A₀ je zrušený, pretože m je celé číslo a funkcia kosínutia sa integruje do celej periódy. 

Integrály obsahujúce produkt cos (n Ω t) cos (m Ω t) sa tiež zrušujú vždy, keď n ≠ m. Iba v prípade, že N = M má integrál:

Všetky výrazy, ktoré majú kosínus znásobený sínus, to znamená, že tie, ktoré sú vynásobené koeficientmi B, pretože obsahujú integrály typu Sen (n Ω T) cos (M Ω T), keď sa definovaný integrál vykonáva na úplnom obdobie. 

Odtiaľ sa dospelo k záveru, že:

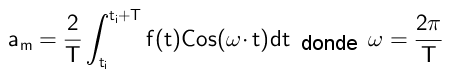
Výpočet koeficientov B

Na nájdenie koeficientov B sa uplatňuje podobný postup, ale tentokrát sa obaja členovia funkcie zhodujú so sériou Fourier vynásobia funkciou SEN (M Ω T).

Z rovnakých dôvodov, ktoré už boli vysvetlené pre prípad, v ktorom je jediný termín, ktorý nie je zrušený po integrácii do úplného obdobia, v ktorom:

n = m

A kde sa objaví integrál [sen (m Ω t)]]², ktoré integrovali v úplnom období, vedie k π.

Môže vám slúžiť: Homografická funkcia: Ako graf, vyriešené cvičenia

Týmto spôsobom sa koeficienty B vypočítajú podľa nasledujúceho vzorca:

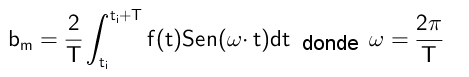
Cvičenia

- Cvičenie 1

Vykonajte explicitný výpočet koeficientov funkcie

 f (t) = 0 áno 0 ≤ t  < π y 1 si π ≤  t   < 2π

Riešenie

Najprv identifikujeme obdobie t tejto funkcie ako 2π, takže základná frekvencia Ω = 2π/ t sa v tomto príklade rovná jednotke, to znamená:

Ω = 1

Funkcia je definovaná v intervale [0, 2π], takže všetky integrácie sa uskutočnia v uvedenom intervale. 

Potom sa nezávislý výraz vypočíta takto:

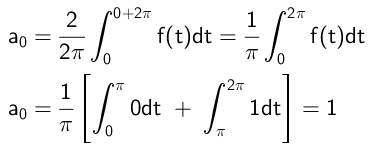
Koeficienty, ktoré sa znásobujú na kosínové funkcie, sa vypočítavajú týmto spôsobom:

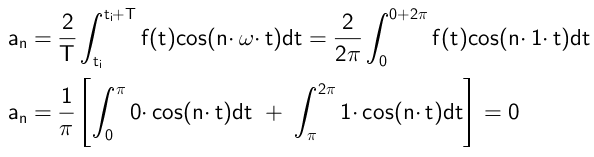
Ako je vidieť, všetky koeficienty pre's sú nulové, čo sa stane za predpokladu, že funkcia f (t) je nepárna.

Podobne sa koeficienty B vypočítajú takto:

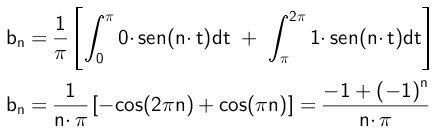
- Cvičenie 2

Nájdite koeficienty funkcie zodpovedajúcej obrázku 1, ktorý je:

f (t) = -1 áno 0

Riešenie 

Keďže funkcia preberá hodnoty medzi -1 a +1, môžeme intuit, aby nezávislý výraz je neplatný, ale výslovne ho vypočítame:

Vzhľadom na to, že funkcia má zvláštnu symetriu, musia byť všetky koeficienty, ktoré znásobujú harmonické výrazy s ksinskou funkciou. Overíme to nižšie:

Nakoniec nájdeme koeficienty B, ktoré znásobujú harmonické výrazy, ktoré obsahujú funkciu sínusu:

Kde je možné si všimnúť všetky B s indexom UP, sú 0. Prvé nepárne výrazy sú:

b₁= -4/(π); b₃= -4/(3π); b₅= -4/(5π); b₇= -4/(7π) a b₉= -4/(9π)

https: // youtu.Be/737yagwszya

Odkazy

1. AMERROR, i. 2013. Zvládnutie diskrétnej Fourierovej transformácie v jednej, dve alebo viacerých dimenziách: nástrahy a artefakty. Springer Science & Business Media.
2. Briggs, w. Devätnásť deväťdesiatpäť. DFT: Príručka vlastníkov pre diskrétnu Fourierovu transformáciu. Siam.
3. Chu, E. 2008. Diskrétne a kontinuálne Fourierové transformácie: analýza, aplikácie a rýchle algoritmy. CRC Press.
4. Guoan BI, Yonghong Zeng. 2012. Transformácie a rýchle algoritmy na analýzu a reprezentácie signálu. Springer Science & Business Media.
5. Sundararajan, D. 2003. Spracovanie digitálneho signálu: teória a prax.Svetový vedecký. 
6. Wikipedia. Fourier Series. Obnovené z: je.Wikipedia.com