Vlastnosti série Fibonacci, prirodzené vzťahy, aplikácie

Ten O séria Dedičstvo fibonacci je sekvencia čísel, ktorá sa získava začiatkom 0 a 1, pokračuje s ich súčtom: 0 + 1 = 1, potom súčet predchádzajúcich dvoch: 1 + 1 = 2 atď.

Podľa tohto postupu sa získajú ďalšie výrazy, pozrime sa: 2 + 1 = 3, 3 + 2 = 5, 5 + 3 = 8, 8 +5 = 13…

Prvé čísla série Fibonacci

Postup sa opakuje toľkokrát, koľkokrát chcete. Týmto spôsobom Fibonacciho dedenie nadobúda formulár: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 .. Čísla, ktoré sa to vyrábajú, sa volajú Fibonacci čísla.

[TOC]

História

Fibonacciho dedenie sa nazýva taliansky matematik, ktorý žil v stredoveku: Leonardo de Pisa, známy tiež ako Fibonacci (1175-1250). 

Leonardo de Pisa

Leonardo strávil detstvom v severnej Afrike a cestoval po celom Stredomorí, kde poznal systém číslovania indo -arabského čísla a bol s ním potešený. Pravdepodobne Leonardov arabskí učitelia ho naučili o dedičstve, ktorého už poznali hinduistickí matematici.

Následne, keď sa vrátil do Pisa Fibonacci, napísal knihu s názvom Liberál (Kniha Abacus), kde okrem zvýraznenia výhod indoarabských čísel voči rímskym číslovaním a zavedeniu 0, vyvolal problém reprodukcie králikov.

A riešením tohto problému je presne počet sukcesie fibonacci.

Leonardo de Pisa nebolo udelené vytvorenie dedenia; Vo svojej knihe sa o ňom zmienil iba ako zvedavosť, ktorá upútala pozornosť mnohých vedcov, ktorí ho nasledovali. Medzi nimi bol francúzsky matematik devätnásteho storočia Edouarda Lucasa, ktorý ju pri štúdiu dedičstva krstil menom stredovekého mudrca, ktorý ho oznámil na Západe.

Problém králikov fibonacci

Problém hovorí: žije pár králikov navždy, čo je o dva mesiace úrodné. Po dosiahnutí zrelosti majú každý mesiac niekoľko detí s rôznym sexom, ktoré tiež trvajú dva mesiace, kým sa reproduku.

Môže vám slúžiť: de Morgan zákony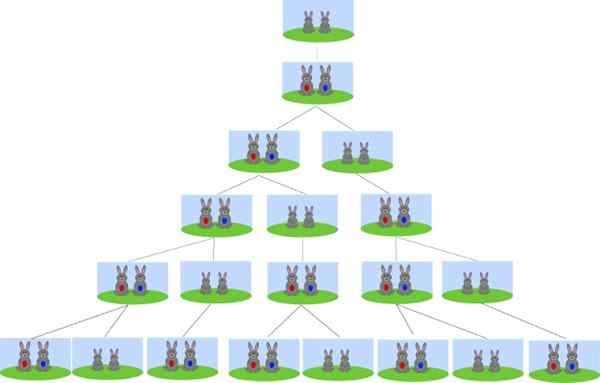Pôvod Fibonacciho dedičstva je v probléme reprodukcie králikov. Zdroj: Wikimedia Commons.

Počnúc niekoľkými novorodencami, koľko párov králikov bude za mesiac? Koľko párov králikov bude po 2, 3 a 4 mesiacoch? A koľko bude po 6 mesiacoch?

Odpoveď je v číslach fibonacci. Po 1 mesiaci sa nachádza 1 pár králikov, pôvodný pár, pretože sa reprodukujú iba po 2 mesiacoch.

Po 2 mesiacoch sú 2 páry králikov: pôvodný pár a ich prvý vrh.

Po 3 mesiacoch budeme mať 3 páry vrátane pôvodného páru, ich prvého vrhu a nového.

Po dosiahnutí 4. mesiaca budeme mať pôvodný pár, prvý vrh, ktorý má svoje prvé deti, vrh tretieho mesiaca a nový odpad. Celkom 5 párov králikov.

Ale to sú čísla sekvencie fibonacci, preto po 6 mesiacoch bude 13 párov králikov, pretože každý mesiac sa pridávajú páry predchádzajúcich dvoch mesiacov.

Vlastnosti série Fibonacci

Tu je niekoľko zaujímavých vlastností dedičstva Fibonacci.

Nehnuteľnosť 1

Rekurzívny vzorec na nájdenie podmienok dedenia je:

do_N+1 = a_n + do_N-1  Pre n väčšie alebo rovné 2.

Kde n = 2, 3, 4, ... to znamená nájsť siedmy termín a₇, Robíme n = 6, takže 6+1 = 7. Potrebujeme poznať podmienky₅  už₆, Zoznam, ktorý je uvedený v úvode do₅ = 5 a a₆ = 8, preto₇ = 5+8 = 13.

Nehnuteľnosť 2

Ak nie sú známe dva výrazy, ktoré chceme nájsť, potom môžeme použiť nasledujúci vzorec:

Môže vám slúžiť: Tesseldos: Charakteristika, typy (pravidelné, nepravidelné), príklady

Nehnuteľnosť 3

Čísla a_n už_N+1 byť  Koprimos, to znamená, že sú to navzájom bratranci, čo znamená, že nemajú spoločné spoločné faktory.

Nehnuteľnosť 4

Veľmi zaujímavou vlastnosťou je kvocient medzi podmienkami_2n už_n, čo má hodnotu 1, keď n = 1. To znamená:

do₂ /₁ = 1

Môžeme to ľahko skontrolovať so zoznamom čísel fibonacci.

Na druhej strane, ak n ≠ 1, potom kvocient je:

do_2n /_n = a_n  + Druhý_N-1

Napríklad ak n = 3, potom a _2n = a₆ = 8 a₃ = 2. Dobre teda:

8/2 = 2 + 2. do₂ = 2 + 2. 1

Naozaj: 8/2 = 4 a 2 + (2.1) = 4. Je možné overiť, či je splnená akúkoľvek hodnota n.

Nehnuteľnosť 5

Pomer r_n = a_N+1 /_{n ,} Keď sa n stane skvelým, zbierajte sa na Dôvod ani Podiel, Iracionálne číslo, ktoré sa často vyskytuje v prírode, dané:

Prirodzené vzťahy dedenia fibonacci

Fibonacciho dedenie v rastlinách

Prejavy dedičstva fibonacci v rastlinnom kráľovstve sa vyskytujú

Pobočky určitých stromov vychádzajú každý rok podľa dedičstva Fibonacci. Prvý rok kmeň rastie bez toho, aby hádzal akúkoľvek pobočku, po jednom roku ju vyrába a tak počas každého roka. Na druhej strane, každá pobočka môže po jednom roku hodiť ďalšiu novú, rovnako ako sa králiky reprodukujú.

Centrum slnečnicových kvetov obsahuje semená usporiadané v logaritmických špirálových lúčoch v oboch zmysle, ktorých množstvá zodpovedajú dvom po sebe idúcim číslam fibonacci.

Fibonacci čísla sú prítomné v počte okvetných lístkov slnečnicových a margaritových kvetov, ako aj v mnohých vzoroch, v ktorých rastliny majú listy.

Môže vám slúžiť: Ordinálna premenná

Odborníci tvrdia, že týmto spôsobom rastliny optimalizujú priestor pre listy a kvety, aby mali optimálny rast.

S ústredným bodom ako východiskovým miestom tieto štruktúry rastú a dostávajú slnečné svetlo, preto musia nové listy a okvetné lístky pokryť čo najmenšie tie, ktoré vyšli ako prvé. A najlepším spôsobom, ako to dosiahnuť, je prijať vzorec rastu z hľadiska sekvencie fibonacci.

Fibonacciho dedenie zvierat

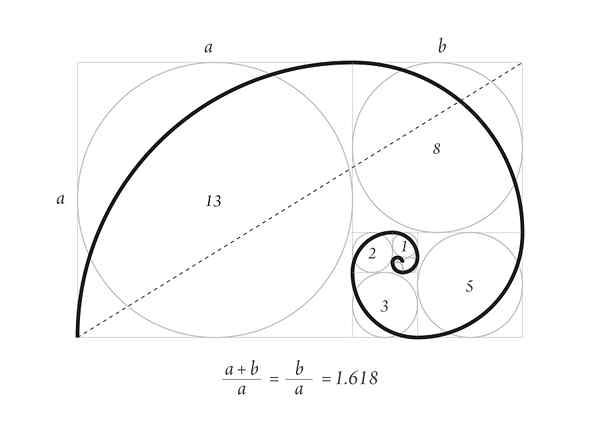Durero špirála s prvým počtom Fibonacciho dedenia

Odolná špirála vynikajúceho obrazu je súčasťou rastu vzoru škrupín u morských zvierat a rohov niektorých prežúvaní.

Začnite s dvoma štvorcami 1, jeden na druhom, potom štvorec strany 2 vedľa neho, ktorý tvorí obdĺžnik strany 3, ktorého strany majú zlatý pomer.

Nižšie je štvorec strany 3 a doľava štvorec strany 5. Nad ňou je štvorec strany 8 a doprava štvorcový strany 13. Toto sú prvé čísla dedenia.

Nakoniec je špirála nakreslená dotykom bodov rohov štvorcov, ako je vidieť na obrázku.

Žiadosti

Fibonacciho dedenie sa uplatňuje v rôznych oblastiach:

-V umení Zlatý podiel súvisiaci s dedením Fibonacci sa objavuje u ľudí a vecí, ktoré predstavujú veľkí umelci ako Leonardo da Vinci, Miguel Ángel a Alberto Durero.

-Proporcie partnera v Aténach tiež reagujú na číslo zlata.

-V kompozíciách Mozarta, Beethovena, Schuberta a Debussyho.

-Navrhnúť objekty, ktorých rozmery vyzerajú harmonicky pre ľudské oči, ako sú kreditné karty, kontajnery, vlajky.

-Na akciovom trhu sa používa na predpovedanie toho, čo ceny vráti svoj trend.

Odkazy

1. Sukcesia fibonacci. Obnovené z: Blogeducastur.je.
2. Stewart, J. 2007. Predbežné vyfarbenie. 5. Vydanie. Učenie sa.
3. Vargas, m. Aplikácie dedičstva fibonacci. Získané z: kamarátov.Cl.
4. Wikipedia. Fibonacci číslo. Zdroj: In.Wikipedia.orgán.