Koncept lineárnych vĺn, charakteristiky, príklady

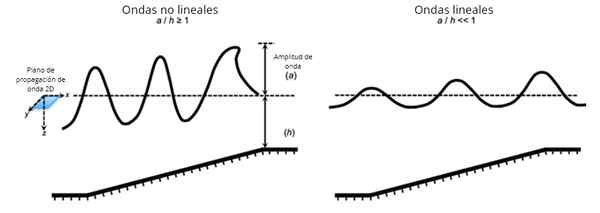
Ten Lineárne vlny Toto sú tie, v ktorých je použiteľný zásada superpozície, tj, v ktorých je možné dosiahnuť vývoj vlny a jej časopriestorový vývoj ako súčet základných riešení, napríklad harmonického typu. Nie všetky vlny spĺňajú zásadu superpozície, ktoré sa s ňou nedodržiavajú.

„Lineárna“ nominálna hodnota vychádza zo skutočnosti, že lineárne vlny vždy spĺňajú diferenciálnu rovnicu v čiastočných derivátoch, v ktorých sú všetky výrazy zahŕňajúce závislú premennú alebo jej deriváty zvýšené na prvú moc.

Vlny, ktoré sú vidieť v diaľke. Zdroj: Pixabay.

Na druhej strane, nelasové vlny spĺňajú vlnové rovnice, ktoré majú kvadratický alebo vyšší stupeň v závislej premennej alebo vo svojich derivátoch.

Niekedy je zmätené lineárne vlny s pozdĺžnymi vlnami, ktoré sú tie, v ktorých sa vibrácie vyskytujú v rovnakom smere šírenia, ako sú napríklad zvukové vlny.

Pozdĺžne vlny, ako aj priečne sa však môžu byť zase lineárne alebo nelineárne v závislosti od iných faktorov, amplitúda počiatočného narušenia a prostredia, v ktorom sa šíria.

Všeobecne sa vyskytuje, že keď je počiatočné narušenie malej amplitúdy, rovnica, ktorá opisuje šírenie vlny, je lineárneho typu alebo sa dá linizovať určitými prístupmi, hoci to nie je vždy také.

[TOC]

Diferenciálna rovnica v lineárnych vlnách

V lineárnom médiu môže byť obmedzený priebeh v priestore a čase reprezentovaný súčtom sínusových alebo kosínových vĺn s rôznymi frekvenciami a vlnovými dĺžkami prostredníctvom série Fourier. 

Lineárne vlny majú vždy diferenciálnu rovnicu priradeného lineárneho typu, ktorého roztok predstavuje predpoveď toho, čo bude narušenie v zadných momentoch počiatočnej ruky umiestnenej priestorovo v počiatočnom počiatočnom okamihu.

Klasická rovnica lineárnych vĺn v jednej priestorovej dimenzii, ktorej roztoky sú lineárne vlny, je:

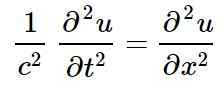
V predchádzajúcej rovnici alebo predstavuje narušenie určitej fyzickej sumy v polohe X A momentálne tón, to znamená alebo Je to funkcia X a tón:

Môže vám slúžiť: Čo sú to vektory Coplanares? (S vyriešenými cvičeniami)

u = u (x, t)

Napríklad, ak ide o zvukovú vlnu vo vzduchu, alebo Môže predstavovať zmenu tlaku vzhľadom na jeho hodnotu bez narušenia.

V prípade elektromagnetickej vlny alebo predstavuje elektrické pole alebo magnetické pole oscilujúce kolmo na smer šírenia.

V prípade napätého lana, alebo predstavuje krížový posun vzhľadom na rovnováhu rovnováhy lana, ako je to znázornené na nasledujúcom obrázku:

Priebeh v danom okamihu, v prípade lineárnych vĺn, táto forma je prekrývanie sínusoidných vĺn rôznych frekvencií a vlnových dĺžok. Zdroj: f. Zapata.

Riešenia diferenciálnej rovnice

Ak máte dve alebo viac roztokov lineárnej diferenciálnej rovnice, každé riešenie vynásobené konštantou bude riešením a bude tiež ich súčtom. 

Na rozdiel od nelineárnych rovníc, Wavelínové rovnice pripúšťajú harmonické riešenia typu: 

alebo₁= A⋅sen (k⋅x - ω⋅t) a alebo₂= A⋅sen (k⋅x + ω⋅t) 

To sa dá overiť jednoduchou substitúciou v rovnici lineárnych vĺn.

Prvé riešenie predstavuje progresívnu vlnu, ktorá postupuje doprava, zatiaľ čo druhá vľavo rýchlo C = Ω/k.

Harmonické riešenia sú charakteristické pre rovnice lineárnych vĺn.

Na druhej strane je lineárna kombinácia dvoch harmonických roztokov tiež riešením rovnice lineárnej vlny: napríklad:

u = a₁ cos (k₁⋅x - Ω₁⋅t) + a₂ drez₂⋅x - Ω₂⋅t) je roztok.

Najdôležitejšou charakteristikou lineárnych vĺn je, že akákoľvek forma vlny, akokoľvek zložitá, sa dá získať súčtom jednoduchých harmonických vĺn v prsníku a kosínus:

u (x, t) = a₀ + ∑_n Do_n cos (k_n⋅x - Ω_n⋅t) + ∑_m B_m drez_m⋅x - Ω_m⋅t).

Disperzné a neisperzívne lineárne vlny

V klasickej rovnici lineárnej vlny, c predstavuje rýchlosť šírenia impulzu.

Nedôverčivé vlny

V prípadoch, kde c Je to konštantná hodnota, napríklad elektromagnetické vlny vo prázdnote, potom pulz v počiatočnom okamihu t = 0 Forma f (x) Šíri sa podľa:

u (x, t) = f (x - c⋅t)

Bez toho, aby ste utrpeli akékoľvek skreslenie. Ak k tomu dôjde, hovorí sa, že médium nie je navrhnuté.

Disperzné vlny

Avšak v disperznom médiu môže šírenie C rýchlosť závisieť od vlnovej dĺžky λ, tj C = C (λ).

Môže vám slúžiť: Rovnica kontinuity

Elektromagnetické vlny sú disperzné pri cestovaní cez materiálové médium. Tiež povrchové vlny vody cestujú rôznou rýchlosťou podľa hĺbky vody.

Rýchlosť, s ktorou sa šíri harmonická vlna A zajtra (k⋅x - Ω⋅t) je Ω/k = c a fázová rýchlosť sa volá. Ak je médium disperzné, potom c Je to funkcia čísla vĺn klimatizovať: C = c (k), kde klimatizovať Súvisí s vlnovou dĺžkou pomocou K = 2π/λ.

Disperzné vzťahy

Vzťah medzi frekvenciou a vlnovou dĺžkou sa nazýva disperzný pomer, ktorá vyjadrila z hľadiska uhlovej frekvencie Ω a číslo vlny klimatizovať je: Ω = c (k) ⋅K.

Niektoré charakteristiky disperzných vzťahov lineárnych vĺn sú nasledujúce:

Vo vlny, v ktorých je vlnová dĺžka (vzdialenosť medzi hrebentami) oveľa väčšia ako hĺbka H, Ale že jeho šírka je oveľa menšia ako hĺbka, že disperzný vzťah je:

Ω = √ (GH) ⋅K

Odtiaľ sa dospelo k záveru, že sa šíria konštantnou rýchlosťou √ (GH) (ne -disperzná polovica).

Vlny vo veľmi hlbokých vodách sú však disperzné, pretože ich disperzný pomer je:

Ω = √ (g/k) ⋅K

To znamená, že fázová rýchlosť Ω/k Je variabilný a závisí od čísla vlny, a teda od vlnovej dĺžky vlny.

Rýchlosť

Ak sa dve harmonické lineárne vlny prekrývajú, ale postupujú rôznymi rýchlosťami, potom rýchlosť skupiny (tj vlne balíka) nezodpovedá fázovej rýchlosti.

Rýchlosť vložka_g Je definovaný ako derivát frekvencie vzhľadom na číslo vlny v disperznom pomere: vložka_g = Ω '(k).

Nasledujúci obrázok ukazuje prekrývanie alebo súčet dvoch harmonických vĺn alebo₁= A⋅sen (k₁⋅x - Ω₁⋅t) a alebo₂= A⋅sen (k₂⋅x - Ω₂⋅t) ktoré cestujú rôznymi rýchlosťami vložka₁= Ω₁/k₁ a vložka₂= Ω₂/k₂. Všimnite si, ako sa rýchlosť skupiny líši od fázovej rýchlosti, v tomto prípade je rýchlosť skupiny ∆Ω/∆K.

Môže vám slúžiť: magnetické vlastnosti materiálov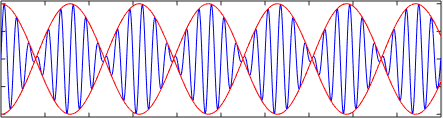Lineárna (modrá) vlna v disperznom médiu. Červená krivka bola pridaná, aby sa zdôraznilo, že rýchlosť skupiny sa líši od rýchlosti šírenia

V závislosti od pomeru disperzie môžu mať fázová rýchlosť a rýchlosť skupiny v opačných smeroch dokonca opačné smery.

Príklady lineárnych vĺn

Elektromagnetické vlny

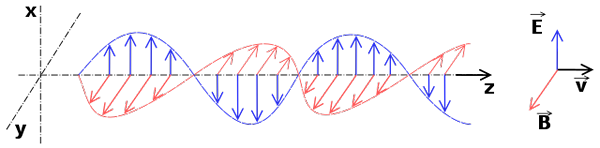elektromagnetické vlny, ktoré tvoria elektromagnetické žiarenie

Elektromagnetické vlny sú lineárne vlny. Jej vlnová rovnica je odvodená z rovníc elektromagnetizmu (Maxwell rovnice), ktoré sú tiež lineárne.

Schrödingerova rovnica

Je to rovnica, ktorá opisuje dynamiku častíc v atómovej stupnici, kde sú relevantné zvlnené charakteristiky, napríklad prípad elektrónov v atóme.

Potom sa volá „elektrónová vlna“ alebo vlnová funkcia, je lineárna vlna.

Vlny v hlbokej vode

Lineárne vlny sú tiež tie, v ktorých je amplitúda oveľa nižšia ako vlnová dĺžka a vlnová dĺžka oveľa väčšia ako hĺbka. Vlny v hlbokej vode sledujú lineárnu teóriu (známe ako Airyho zvlnená teória).

Vlna, ktorá sa blíži k pobrežiu a tvorí charakteristický hrebeň, ktorý je valcovaný (a že miluje surferi), je nelineárna vlna.

Znieť

Pretože zvuk je malým narušením atmosférického tlaku, považuje sa za lineárnu vlnu. Nárazová vlna výbuchu alebo čela vlny nadzvukovej roviny je však typickými nelineárnymi vlnami príkladov.

Vlny na napätom lane

Vlny, ktoré sa šíria napätým lanom, sú lineárne za predpokladu, že počiatočná pulzácia je malá, to znamená, že elastický limit lana nie je prekročený.

Lineárne vlny na reťazcoch sa odrážajú na ich koncoch a prekrývaní sa, čo vedie k stacionárnym vlnám alebo vibračným režimom, ktoré dávajú harmonické a podskupinové tóny charakteristické pre strunové prístroje.

Odkazy

1. Griffiths G a Schiesser W. Lineárne a nelineárne vlny. Získané z: Sholarpedia.orgán.
2. Whitham g.B. (1999) „Lineárne a nelineárne vlny“. Mravný. 
3. Wikipedia. Nelineárne vlny. Obnovené z: je.Wikipedia.com
4. Wikipedia. Nelineárny akustický. Zdroj: In.Wikipedia.com
5. Wikipedia. Vlny. Zdroj: In.Wikipedia.com
6. Wikiwaves. Nelineárne vlny. Získané z: wikiwaves.orgán