Fyzický

Polkruh Ako vypočítať obvod, oblasť, stredisko, cvičenia

Polkruh Ako vypočítať obvod, oblasť, stredisko, cvičenia

On polkruh Je to plochá postava vymedzená priemerom obvodu a jeden z dvoch plochých kruhových oblúkov určených uvedeným priemerom.

Týmto spôsobom je polkruh ohraničený a polkruh, ktorý pozostáva z plochého kruhového oblúka a priameho segmentu, ktorý spája konce plochého kruhového oblúka. Polkruh pokrýva polkruh a všetky vnútorné body na rovnaké.

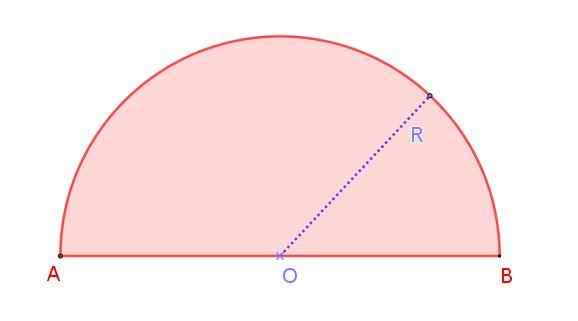
postava 1. Rádio Rádio kruh. Zdroj: f. Zapata.

Vidíme to na obrázku 1, ktorý zobrazuje rádio Rión R, ktorého opatrenie je polovica priemeru AB. Všimnite si, že na rozdiel od kruhu, v ktorom sú nekonečné priemery, v polkruhu je iba jeden priemer.

Polkruh je geometrická postava s mnohými použitiami v architektúre a dizajne, ako vidíme na nasledujúcom obrázku:

Obrázok 2. Seminicírculo ako dekoratívny prvok v architektúre. Zdroj: Pikist.

[TOC]

Prvky a opatrenia polkruhu

Prvky polkruhu sú:

1.- Plochý kruhový oblúk a⌒b

2.- Segment [AB] 

3.- Interiér ukazuje na polkruh zložený z oblúka A⌒B a segmentu [AB].

Obvod polkruhu

Obvod je súčet obrysu oblúka plus súčet priameho segmentu:

Obvod = dĺžka oblúka A⌒B + Dĺžka segmentu [AB]

V prípade rádiového polkruhu R, jeho obvod P bude daný vzorcom:

P = π⋅r + 2 št = (π + 2) ⋅r

Prvým termínom je polovica obvodu obvodu polomeru, zatiaľ čo druhý je dĺžka priemeru, ktorý je dvojnásobkom polomeru.

Môže vám slúžiť: teplometrické stupnice

Plocha polkruhu

Keďže polkruh je jedným z plochých uhlových sektorov, ktoré zostávajú vtiahnutím priemeru cez obvod, jeho oblasť A bude polovica kruhovej oblasti, ktorá obsahuje rádiové polkruh R:

A = (π⋅r2) / 2 = ½ πple2

Ťažba polkruhu

Centroid polkruhu je na jeho osi symetrie do výšky meranej od jej priemeru 4/(3π) krát polomer r.

Zodpovedá to približne 0,424 škomorodom, meraným od stredu polkruhu a na jeho osi symetrie, ako je znázornené na obrázku 3.

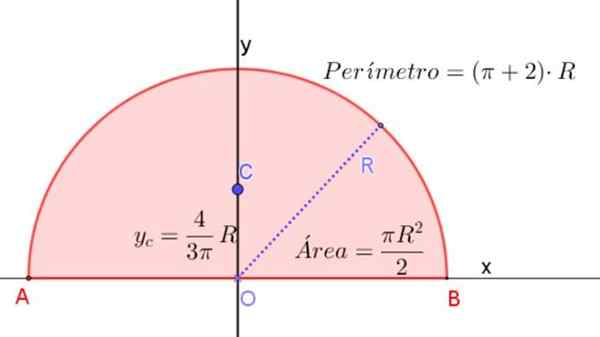Obrázok 3. Polkruh Rádiu R, čo naznačuje vzorce na určenie oblasti, obvodu a umiestnenia jeho centiap. Zdroj: f. Zapata.

Moment zotrvačnosti polkruhu

Moment zotrvačnosti plochej postavy je definovaný vzhľadom na os, napríklad os x, napríklad:

Integrál štvorca vzdialenosti bodov, ktoré patria k obrázku k osi, pri. 

Obrázok 4 zobrazuje definíciu momentu zotrvačnosti iX polkruhu rádio R, vzhľadom na os x, ktorá prechádza jej diagonálom:

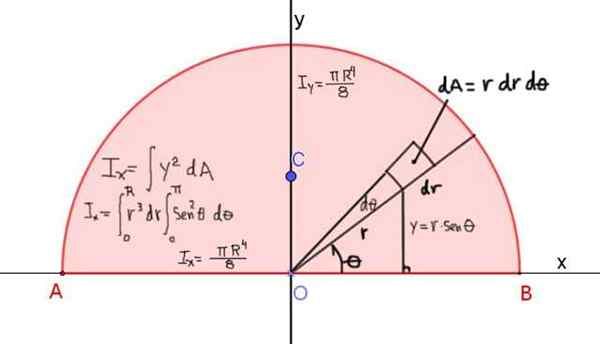Obrázok 4. Definícia momentu zotrvačnosti IX polkruhu vzhľadom na os x, ktorá prechádza cez jej diagonálne. Výsledok je uvedený pre momenty zotrvačnosti vzhľadom na os x a y. Zdroj: f. Zapata.

Moment zotrvačnosti vzhľadom na os x je daný:

JoX = (π⋅r4) / 8

A okamih zotrvačnosti vzhľadom na os symetrie a je:

Môže vám slúžiť: zvlnená optika

Iy = (π⋅r4) / 8

Ukazuje, že oba momenty zotrvačnosti sa zhodujú vo svojom receptúre, ale je dôležité zdôrazniť, že sa odvolávajú na rôzne osi.

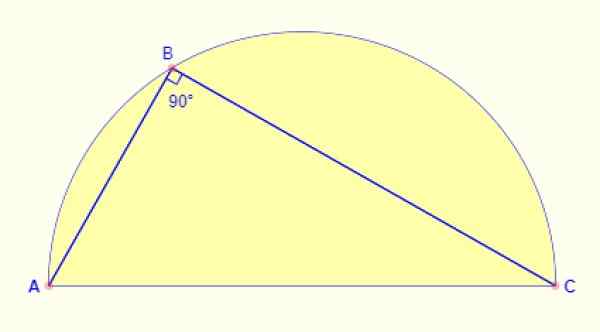
Registrovaný uhol

Uhol registrovaný v polkruhu je vždy 90 °. Bez ohľadu na to, ktorá časť oblúka je odvedená do bodu, uhol, ktorý sa tvorí medzi strany AB a BC postavy, je vždy rovný.

Obrázok 5. Uhol zaregistrovaný v polkruhu. Zdroj: Math Open Reference.

Vyriešené cvičenia

Cvičenie 1 

Stanovte obvod polkruhu polomeru 10 cm.

Riešenie

Pripomeňme, že obvod v závislosti od polomeru je daný vzorcom, ktorý sme predtým videli:

P = (2 + π) ⋅r

P = (2 + 3,14) ⋅ 10 cm = 5,14 ⋅ 10 cm = 51,4 cm.

Cvičenie 2

Nájdite plochu 10 cm rádiového polkruhu.

Riešenie

Vzorec pre oblasť polkruhu je:

A = ½ πple2 = ½ πple (10 cm)2 = 50π cm2 = 50 x 3,14 cm2 = 157 cm2.

Cvičenie 3

Stanovte výšku H stredu polomeru polkruh R = 10 cm meraný z jej základne, čo je to isté, čo je priemer polkruhu. 

Riešenie

Centroid je polkruhový rovnovážny bod a jeho poloha je na osi symetrie vo výške H základne (priemer polkruhu):

H = (4 št) / (3π) = (4,10 cm) / (3 x 3,14) = 4 246 cm

Cvičenie 4

Nájdite moment zotrvačnosti polkruhu vzhľadom na os, ktorá sa zhoduje s jej priemerom, s vedomím, že polkruh je vyrobený z tenkého plechu. Jeho polomer je 10 cm a jeho hmotnosť je 100 gramov.

Riešenie

Vzorec, ktorý dáva okamih zotrvačnosti polkruhu, je:

Môže vám slúžiť: Fyzika tuhého štátu: vlastnosti, štruktúra, príklady

JoX = (π⋅r4) / 8

Ale ako nám problém hovorí, že ide o materiálový polkruh, potom sa musí predchádzajúci vzťah vynásobiť povrchovou hustotou hmotnosti polkruhov, ktorá bude označená σ.

JoX = σ (π⋅r4) / 8

Potom určíme σ, čo nie je nič iné ako hmotnosť polkruhu rozdelenej medzi oblasť rovnakej oblasti.

Táto oblasť bola stanovená v cvičení 2 a výsledok bol 157 cm2. Potom bude povrchná hustota tohto polkruhu:

σ = 100 gramov / 157 cm2 = 0,637 g/cm2

Potom sa okamih zotrvačnosti vzhľadom na priemer bude vypočítaný nasledovne:

JoX = (0,637 g/cm2) [3,1416 ⋅ (10 cm)4]/ 8

Výsledné:

JoX = 2502 gacm2

Cvičenie 5

Určite moment zotrvačnosti polomeru polkruh 10 cm postavený z materiálového listu s povrchovou hustotou 0,637 g/cm2 osou, ktorá prechádza cez jej ťažisko a je rovnobežná s jej priemerom.

Riešenie

Na vyriešenie tohto cvičenia je potrebné si zapamätať Steinerovu vetu vo chvíľach zotrvačnosti paralelných osí, čo hovorí:

Moment zotrvačnosti i vzhľadom na os, ktorá je vo vzdialenosti h ťažiska, sa rovná súčtu momentu zotrvačnosti ic Pokiaľ ide o os, ktorá prechádza strediskom a je rovnobežná s prvou ďalšou produktom cesta cez štvorec oddelenia týchto dvoch osí.

I = ic + M h2

V našom prípade je známe, že je to okamih zotrvačnosti vzhľadom na priemer, ktorý bol už vypočítaný v cvičení 4. H tiež vie medzi priemerom a ťažiskom, ktorý bol vypočítaný v cvičení 3.

Musíme len vyčistiť IC:

Joc = I - m h2

Joc = 2502 gacm2 - 100 g ⋅ (4 246 cm)2 Výsledkom je okamih zotrvačnosti osou rovnobežnou s priemerom a ktorý prechádza centroidom je: 

Joc = 699,15 g⋅cm2

Odkazy

  1. Alexander, D. 2013. Geometria. 5. Vydanie. Učenie sa.
  2. Matematika otvorená referencia. Polkruh. Získané z: Mathpenref.com.
  3. Vesmír.Polkruh. Získané z: Universoformulas.com.
  4. Vesmír. Plocha polkruhu. Získané z: Universoformulas.com.
  5. Wikipedia. Polkruh. Zdroj: In.Wikipedia.com.