Vysvetlenie druhej rovnováhy, príklady, cvičenia

Ten Druhá rovnovážna podmienka Tvrdí, že súčet krútiacich momentov alebo momentov produkovaných všetkými silami, ktoré pôsobia na tele, bez ohľadu na to, aký bod sa vypočítava, musí byť zrušený tak, aby bolo uvedené telo v statickej alebo dynamickej rovnováhe.

Označovanie krútiaceho momentu alebo momentu sily prostredníctvom gréckeho listu τ, Matematicky sa vyjadruje takto:

∑ τ = 0

postava 1. Na vyváženie kolíka je potrebné použiť druhú rovnovážnu podmienku. Zdroj: pxhere.

Odvážny list označuje vektorovú povahu okamihu, ktorý sa musí zrušovať vzhľadom na akýkoľvek bod, ktorý je vybraný ako spin centrum. Týmto spôsobom je zaručené zrušením momentu čistého krútia.

Ak sa však objekt už predtým otáčal a sieťový krútiaci moment náhle zmizne, rotácia bude pokračovať, ale s konštantnou uhlovou rýchlosťou.

Druhá rovnovážna podmienka sa používa v spojení s prvou podmienkou, ktorá hovorí, že súčet síl na tele musí byť neplatný, takže sa nepohybuje alebo že ak áno, je to s rovnomerným priamym pohybom:

∑ F = 0

Obe podmienky sa vzťahujú na rozšírené telá, ktoré sú merateľné rozmery. Ak má byť objekt časticou, nemá zmysel hovoriť o rotáciách a prvá podmienka na zaručenie rovnováhy je dostatočná.

Príklady

Druhá rovnovážna podmienka je odhalená v nespočetných situáciách:

Pri lezení po schodoch

Pri podopretí schodiska na podlahe a stene potrebujeme dosť na trieť, najmä na podlahu, aby sme zaistili, že schodisko skĺzne. Ak sa pokúsime vyliezť na rebrík podopretý na mastnej, mokrej alebo klzkej podlahe, nie je ťažké predvídať, že padneme.

Aby ste boli schopní schodisko schodistne používať, je potrebné, aby bol v statickej rovnováhe počas lezenia a keď je potrebný v kroku.

Môže vám slúžiť: pluto (trpaslík planéta)

Pohyb skrinky

Ak chcete presunúť vysoký nábytok ako skrinku alebo akýkoľvek kus, ktorého vysoký je väčší ako jeho široký, je vhodné tlačiť na nízky bod, aby sa predišlo prevráteniu, týmto spôsobom je pravdepodobnejšie, že nábytok sa namiesto toho skĺzne otáčania a ľahnúť si.

Za týchto okolností nie je nábytok nevyhnutne v rovnováhe, pretože by sa mohol pohybovať rýchlo, ale aspoň by sa neotáčal.

Balkón

Balkóny, ktoré vynikajú, musia byť budovy postavené a zaručujú, že hoci je veľa ľudí na vrchole, neotáča sa a zrúti sa.

Dielektrika v externých elektrických poliach

Pri umiestnení dielektrického materiálu do vonkajšieho elektrického poľa sa molekuly pohybujú a otáčajú, aby prijali rovnovážnu polohu, čím sa vytvorí elektrické pole vo vnútri materiálu.

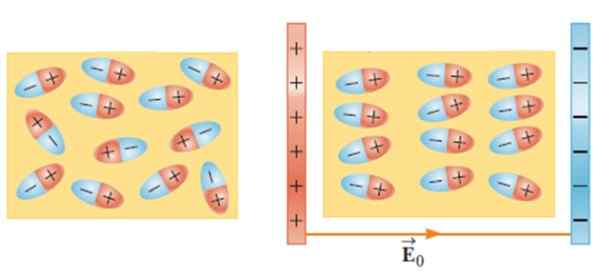Obrázok 2.- Bez externého elektrického poľa sú dipóly randomizované (vľavo). Vonkajšie pole aplikuje krútiaci moment na dielektrické molekuly a tieto sú reorganizované. Zdroj: Serway, r. Fyzika pre vedu a inžinierstvo.

Tento efekt spôsobuje, že kapacita kondenzátora sa zvýši, keď sa medzi jeho brnenie zavádza materiál ako sklo, guma, papier alebo olej.

Znaky a lampy

Je bežné, že mnohé priestory zavesia oznámenia na stene budovy, takže sú viditeľné pre okoloidúcich.

Plagát je pripevnený tyčou a káblom, obidve pripevnené na stene pomocou opory. Rôzne sily, ktoré sa konajú, musia zabezpečiť, aby plagát nespadol, pre ktoré sa dve rovnovážne podmienky dostanú do činnosti.

Reflektor v parku môže byť tiež umiestnený týmto spôsobom, ako na nasledujúcom obrázku:

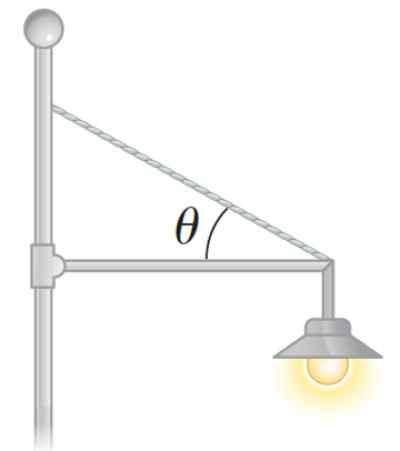Obrázok 3. Statická vyvážená žiarovka. Zdroj: Serway. Fyzika pre vedu a inžinierstvo.

Ako vypočítať moment siete alebo sieťový moment sily?

Krútiaci moment alebo moment sily, označený τ ani M V niektorých textoch sa vždy vypočíta s ohľadom na určitý bod, keď os rotácie prechádza.

Je definovaný ako vektorový produkt medzi vektorom polohy r, to je nasmerované z uvedenej osi do bodu použitia sily a sily F:

Môže vám slúžiť: termodynamická rovnováha: triedy a aplikácie

τ = r × F

Ako vektor je potrebné vyjadriť krútiaci moment, ktorý dáva jeho veľkosť, smer a význam. Veľkosť je daná:

τ = RF.hriech

Správne pravidlo pre vektorový produkt

Ak je problém v rovine, adresa krútiaceho momentu je kolmá na papier alebo obrazovku a smer je určený pravidlom pravej ruky, v ktorej index smeruje smerom k r, Prostredný prst smerom k F a palec signály do alebo z papiera.

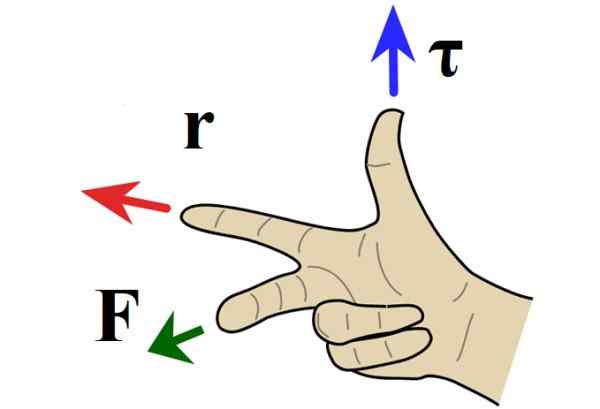Obrázok 4. Pravá pravidlo pre vektorový produkt. Zdroj: Wikimedia Commons.

Keď krútiaci moment poukazuje z papiera, rotácia je v opačnom smere ako ihly a priradí sa kladné znamenie z dohovoru. Ak je moment namiesto toho nasmerovaný v hárku, rotácia je v smere rúk a negatívna značka.

Na nájdenie čistého krútiaceho momentu je zvolený vhodný bod pre výpočet, ktorý môže byť ten, v ktorom najväčšie množstvo síl pôsobí. V tomto prípade je moment týchto síl neplatný, pretože má vektor polohy r veľkosti 0.

Môžete si vybrať akýkoľvek bod, ktorý ponúka dostatok informácií na vyčistenie neznámeho, ktorý žiada, aby sa problém vyriešil. Pozrime sa to potom podrobnejšie.

Cvičenie

Reflektor nasledujúceho obrázku má 20 kg hmotnosti a je podopretý vodorovnou tenkou tyčou, opovrhnutiaou hmotnosťou a dĺžkou L, ktorá je vyjadrená na stĺp. Kábel, tiež svetlo, čo pomáha udržať reflektor tvorí uhol 9 = 30 ° s tyčou. Vypočítať:

a) napätie v kábli

b) veľkosť sily F, ktorú stĺp vyvíja na tyč cez záves.

Riešenie

Použijeme prvú rovnovážnu podmienku ∑ F = 0 na sily uvedené v diagrame:

Môže vám slúžiť: Absorbované teplo: vzorce, ako ho vypočítať a vyriešiť cvičenia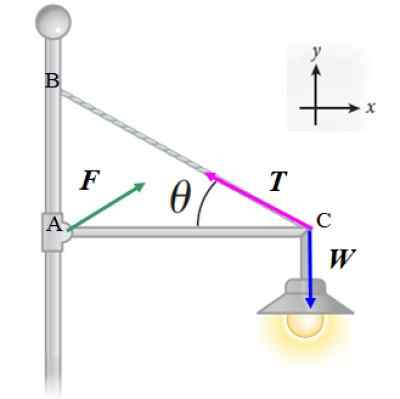

F + Tón + W = 0

Všimnite si, že veľkosť a smer F Ešte sa musia určiť, ale predpokladáme, že má dve zložky: f_X a f_a. Týmto spôsobom dostávame dve rovnice:

F_X -Tón. cos θ = 0

F_a - W + tlek sin θ = 0

Teraz aplikujme druhú rovnovážnu podmienku a výber bodu A, pretože nepoznáme veľkosť F ani to Tón. Pri výbere tohto bodu vektor r_Do je neplatný, preto okamih F je neplatný a veľkosť F V rovnici sa neobjaví:

-W⋅l + t⋅sen θ⋅l = 0

Preto:

Tón.hriech.L = w.L

T = w/sen θ = (20 kg x 9.8 m/s²) / Sin 30 ° = 392 n

Poznanie veľkosti t môžeme vyčistiť komponent f_X:

F_X = Tlek cos θ = 392 cos 30 ° n = 339. 5 n

A potom komponent f_a:

F_a = W - t⋅ sin θ = (20 kg x 9.8 m/s²) - 392⋅sen 30 ° = 0

Potom môžeme vyjadriť F Tak:

F = 339.5 n X

Je to preto vodorovná sila. Je to preto, že sa domnievame, že bar mal opovrhnuteľnú váhu.

Ak bol bod C vybraný na výpočet výsledného momentu, vektory r_Tón a r_W Sú preto nulové, preto:

M = f_YlekL = 0

Dospelo sa k záveru, že f_a = 0. Teda:

- W + tlek sin θ = 0

T = w/ sin 9

Čo je rovnaký výsledok pôvodne získaný výberom bodu A ako miesto, kde os rotácie prechádza.

Záujmové témy

Rovnováha.

Podmienka prvého vyváženia.

Odkazy

1. Bedford, 2000. Do. Mechanika pre inžinierstvo: statické. Addison Wesley.
2. Figueroa, D. (2005). Séria: Fyzika pre vedu a inžinierstvo. Zväzok 4. Častice. Editoval Douglas Figueroa (USB).
3. Giancoli, D.  2006. Fyzika: Princípy s aplikáciami. 6. Ed Prentice Hall.
4. Sears, Zemansky. 2016. Fyzika univerzity s modernou fyzikou. 14. Edimatizovať. Zväzok 1.
5. Serway, r., Jewett, J. (2008). Fyzika pre vedu a inžinierstvo. Zväzok 1. 7. Edimatizovať. Učenie sa.