Uhly v typoch obvodov, vlastnosti, cvičenia vyriešené

Nazývaný Uhly obvodu pre tých, v ktorých je niektorý z jeho prvkov alebo sa pretína pri danom obvode. Medzi nimi sú tieto:

1.- On centrálny uhol, ktorého vrchol je v strede obvodu a jeho strany naň sušia, ako vidíme na nasledujúcom obrázku:

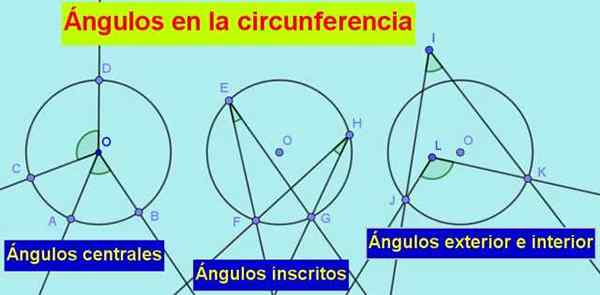
postava 1. Typy uhlov v obvode sú: centrálne, vpísané, vonkajší a interiér. Zdroj: f. Zapata.

2.- On registrovaný uhol, ktorého vrchol je na obvode a jeho strany sú suché alebo dotyčené k obvodu.

3.- Vonkajší uhol, ktorého vrchol je mimo obvodu, ale jeho strany sú suché alebo dotyčené k obvodu.

4.- On Vnútorný, s vrcholom vo vnútri obvodu a jeho suchým stranami.

Všetky tieto uhly si navzájom udržiavajú určité vzťahy, čo nás vedie k dôležitým vlastnostiam medzi uhlami patriacimi k danému obvodu.

[TOC]

Vlastnosti

- Centrálny uhol

Centrálny uhol je definovaný ako ten, ktorého vrchol je v strede obvodu a jeho strany sa rozrezajú do obvodu.

Radiány Miera centrálneho uhla je kvocient medzi oblúkom, ktorý je obvodom obvodu medzi bokmi uhla a polomerom obvodu. 

Ak je obvod jednotný, to znamená polomer 1, potom miera centrálneho uhla je dĺžka oblúka, čo zodpovedá počtu radiánov.

Ak chcete mieru centrálneho uhla v stupňoch, potom sa miera vynásobí v radiánoch faktorom 180 °/π.

Nástroje na meranie uhlov, ako je transportér a goniometer, vždy používajú centrálny uhol a dĺžku podteku.

Môže vám slúžiť: čiastočné deriváty: vlastnosti, výpočet, cvičenia

Sú kalibrované v sexuálnych stupňoch, čo znamená, že vždy, keď sa s nimi meria uhol, v zadnej časti je meraná dĺžka oblúka podvedeného centrálnym uhlom.

Nehnuteľnosť

Miera centrálneho uhla v radiánoch sa rovná dĺžke oblúka, ktorý subtínky alebo zachytávajú delené dĺžkou polomeru.

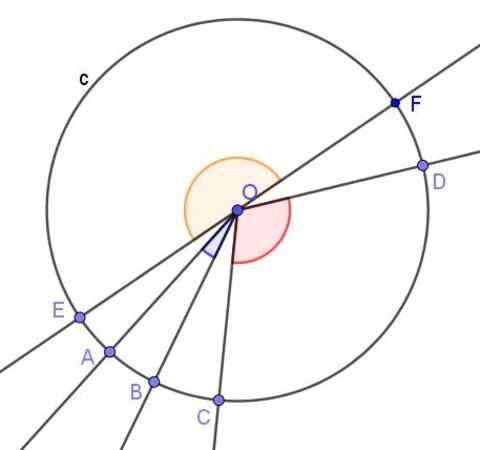Obrázok 2. Sú zobrazené tri centrálne uhly. Jeden akútny, druhý tupý a jeden plochý. Zdroj: f. Zapata.

- Registrovaný uhol

Registrovaný uhol obvodu je ten, ktorý má svoj vrchol na obvode a jeho polopriepustné sú suché alebo dotyčené do toho istého. 

Jeho vlastnosti sú:

Vlastnosti

-Registrovaný uhol je konvexný alebo plochý.

-Keď vpísaný uhol zachytí rovnaký oblúk ako centrálny uhol, miera prvého bude polovicou odhodlania druhého.

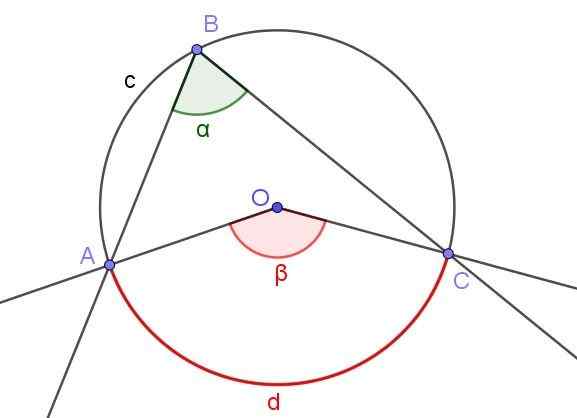Obrázok 3. Registrovaný uhol ∠ABC a centrálny uhol ∠AOC, ktorý subtituje rovnaký oblúk A⌒C. Zdroj: f. Zapata.

Obrázok 3 zobrazuje dva uhly ∠ABC a ∠AOC, ktoré zachytia rovnaký obvod Arc A⌒C.

Ak je miera registrovaného uhla a, potom je β miera centrálneho uhla dvojnásobkom miery registrovaného uhla (β = 2 a), pretože obe odpočítajú rovnaký nameraný oblúk d.

- Vonkajší uhol

Je to uhol, ktorého vrchol je mimo obvodu a každá z jeho strán sa znižuje obvodu v jednom alebo viacerých bodoch.

Nehnuteľnosť

-Jeho miera sa rovná semi -expresii (alebo rozdielom rozdeleným 2) centrálnych uhlov, ktoré zachytávajú oblúky samotné.

Aby sa zabezpečilo, že opatrenie je pozitívne, semi -expresia by mala byť vždy centrálnym uhlom najväčšieho opatrenia menej mierou dolného centrálneho uhla, ako je znázornené na nasledujúcom obrázku.

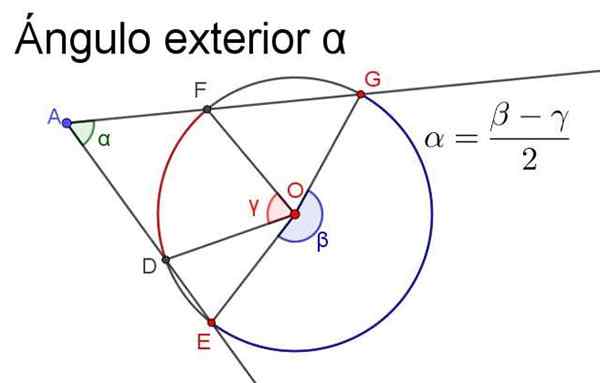Obrázok 4. Vonkajší uhol a je rovný semifinále centrálov, ktoré podriadia rovnaké oblúky. Zdroj: f. Zapata.

- Vnútorný

Vnútorný uhol je ten, ktorého vrchol je vo vnútri obvodu a jeho strany sa znížia na obvod.

Môže vám slúžiť: určovací koeficient: vzorce, výpočet, interpretácia, príklady

Nehnuteľnosť 

Jeho miera sa rovná semi -stope centrálneho uhla, ktorý podvádza rovnaký oblúk, plus centrálny uhol, ktorý podvádza rovnaký oblúk ako jeho predĺženie uhla (toto je vnútorný uhol tvorený polopriepustný vnútorný uhol).

Nasledujúci obrázok zobrazuje a objasňuje vlastnosť vnútorného uhla.

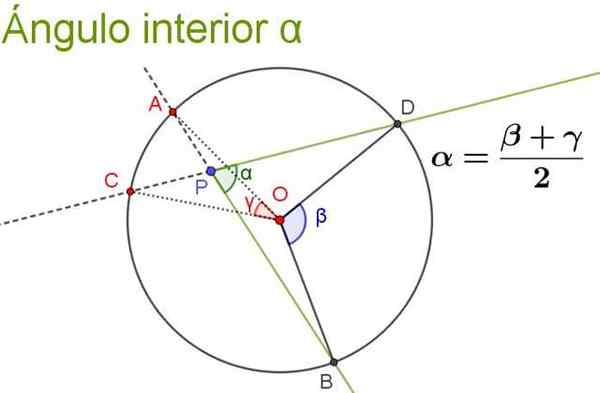Obrázok 5. V vnútornom uhle sa rovná semi -seismu centrálnych uhlov, ktoré podriadia rovnaké oblúky ako on sám. Zdroj: f. Zapata.

Vyriešené cvičenia

- Cvičenie 1

Predpokladajme, že vpísaný uhol, v ktorom jedna zo strán prechádza stredom obvodu, ako je znázornené na obrázku 6. Polomer obvodu je OA = 3 cm a oblúk má dĺžku π/2 cm. Stanovte hodnotu a a β uhlov.

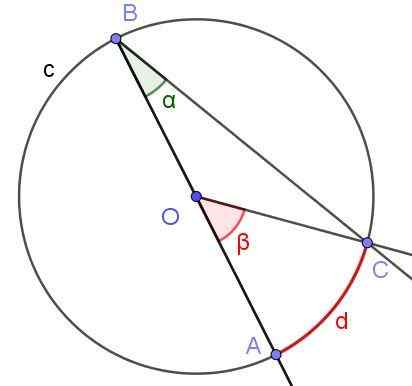Obrázok 6. Registrovaný uhol ∠ABC s bočnou stránkou [BA) cez O a centrálny uhol ∠AOC.Zdroj: f. Zapata.

Riešenie

V tomto prípade sa tvorí COB Isosceles Triange, pretože [OC] = [OB]. V trojuholníku Isosceles sú uhly susediace s základňou rovnaké, preto musia ∠BCO = ∠ABC = α. Na druhej strane ∠COB = 180 ° - β. Berúc do úvahy súčet vnútorných uhlov klasického trojuholníka, ktorý máte:

a + a + (180 ° - p) = 180 °

Odkiaľ vyplýva, že 2 a = β alebo čo je ekvivalentné a = β/2, čo potvrdzuje vlastnosť (3) predchádzajúcej časti, že miera registrovaného uhla je polovica centrálneho uhla, keď oba uhly odpočítajú rovnaké lano [AC].

Teraz pokračujeme v určovaní numerických hodnôt: Phel β je ústredný a jeho miera v Radianoch je pomer medzi oblúkom D a polomerom R = OA, takže jeho miera je:

p = d / r = (π / 2 cm) / (3 cm) = π / 6 rad = 30 °.

Môže vám slúžiť: štvornásobné: prvky, vlastnosti, klasifikácia, príklady

Na druhej strane už bolo potvrdené, že a = β / 2 = (π / 6 rad) / 2 = π / 12 rad = 15 °. 

- Cvičenie 2

Na obrázku 7 uhly α₁ a p₂ mať rovnaké opatrenie. Okrem toho uhol β₁ Meria 60 °. Stanovte uhly β a a.

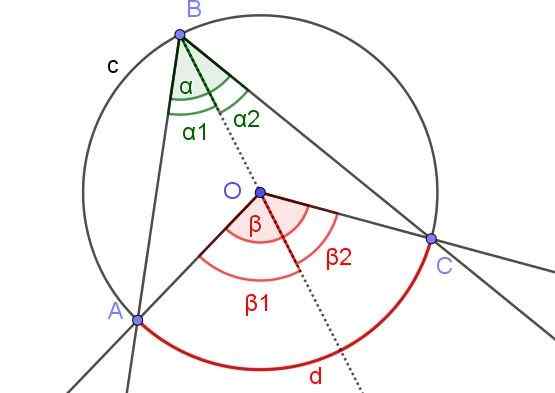Obrázok 7. Na obrázku a₁ = β₂ a p₁ = 60 °. Stanovte hodnoty β a a. Zdroj: f. Zapata.

Riešenie

V tomto prípade je vpísaný uhol ∠ABC, v ktorom je stred alebo obvod vo vnútri uhla.

Kvôli majetku (3) máte α₂ = β₂ /2 a α₁ = β₁ /2. Ako:

α = α₁ + α₂ a p = β₁ + p₂

Máte preto:

α = α₁ + α₂ = β₁ /2 + β₂ /2 = (β₁ + p₂) / 2 = β / 2.

To znamená podľa vlastností:

a = β / 2

Ako sa hovorí, že β₁ = 60 ° potom:

α₁ = β₁ / 2 = 60 ° / 2 = 30 °.

Tiež nám hovoria, že α₁ = β₂ Takže to vyplýva, že:

p₂ = 30 °.

Uhol β je:

p₁ + p₂ = 60 ° + 30 ° = 90 °.

A ako a = β / 2, potom:

a = 90 ° / 2 = 45 °. 

Na záver:

p = 90 ° a a = 45 °.

Odkazy

1. Baldor, a. 1973. Geometria a trigonometria. Stredoamerický kultúrny úvodník.
2. A. Do. 2003. Elementy geometrie: s cvičeniami a geometria kompasu. University of Medellin.
3. Geometria 1. Uhly v obvode. Získané z: edu.Xunta.je.
4. Všetka veda. Vyriešené cvičenia uhlov v obvode. Získané z: Francesphysics.Blog.com
5. Wikipedia. Registrovaný uhol. Obnovené z: je.Wikipedia.com