Pravidlo páky

Čo je pravidlo páky?

Ten pravidlo páky Je to matematický postup, ktorý umožňuje vypočítať frakcie, percentá alebo množstvá fáz prítomných v rovnováhe v binárnom systéme. Nielenže je to matematické, ale tiež dosť grafické a asertívne, je veľmi užitočné pri výpočtoch fyzikálno -chemických a inžinierstva.

Toto pravidlo sa vzťahuje na fázové diagramy pre binárne systémy, bez ohľadu na typ systému samotného systému. To znamená, že fázy môžu byť pevné, rovnako ako v prípade zliatiny; alebo kvapalné a plynné, ako vidíme v systémoch v rovnováhe kvapaliny.

Fyzikálny a matematický princíp páky sa používa aj na chemické účely a vo fyzike materiálov. Zdroj: Jimbowley, CC BY-SA 3.0, cez Wikimedia Commons

Pravidlo páky sa môže uplatniť priamo, berúc do úvahy hodnoty grafiky v osi Abscissa, kde globálne frakcie alebo percentuálne podiely najprchavejšej zložky zvyčajne idú v prípade kvapalín; alebo žiaruvzdorné, v prípade kovov v zliatinách.

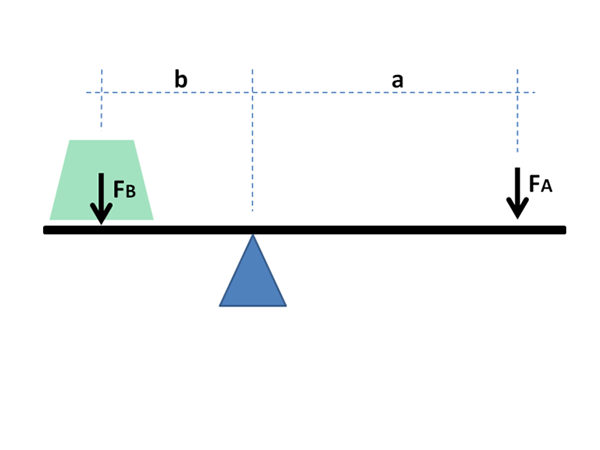
Ako bude uvedené nižšie, jeho názov je spôsobený obrovskou podobnosťou, ktorú má s matematickými výrazmi, ktoré demonštrujú rovnováhu medzi dvoma masami umiestnenými na koncoch rockeru s Fulcro.

Army páky musia vyvážiť, aby vyvážili masy záťaže; V prípade fázových diagramov, frakcie a mólov fáz v rovnováhe materiálu.

Vysvetlenie

Grafické aspekty

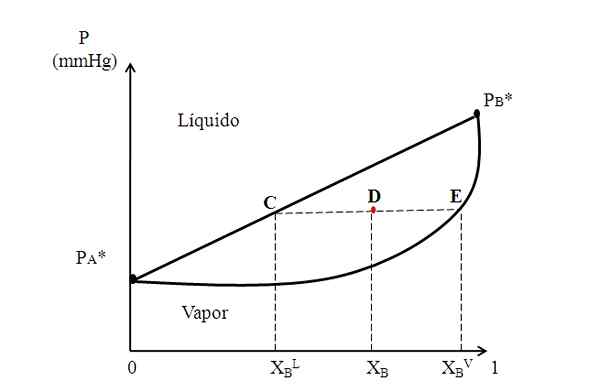Hypotetický binárny diagram, kde väzobná čiara ukazuje zloženie kvapalných a parných fáz. Zdroj: Gabriel Bolívar.

V strede vyššie uvedeného diagramu máme oblasť, v ktorej koexistujú tekuté a pary; to znamená, že rovnovážna oblasť kvapaliny. Nad touto oblasťou bude zmes A a B tekutá a pod ňou bude sóda kvôli nižším tlakom.

Teraz zvážte zmes so zložením X_B a ktorého tlak ho umiestni v bode D. Vytiahneme z bodu D horizontálna čiara, ktorá sa dotýka čiary a krivky po stranách, pôvodom bodov C a E, respektíve. Táto línia, ktorá oznamuje body C, D a E, C-D-E, je línia známa ako línia Únie a premietaním do osi a musí nám dať tlak systému.

Môže vám slúžiť: Vodná alkalita: Čo je, odhodlanie a význam

Potom z týchto bodov nakreslíme ďalšie čiary kolmé na väzobnú čiaru, ktorá bude hrať os x. Keď bod E spočíva na parnej krivke, potom budeme mať molárnu frakciu B vo fáze pary (x_B^Vložka). Podobne nám bod C na priamke kvapaliny dá molárnu frakciu B v kvapalnej fáze (x_B^L).

Pravidlo páky je založené presne na väzbovej čiare a vzdialenosti medzi x_B^L, X_B a x_B^Vložka.

Matematický odpočet

Globálna molárna frakcia B sa rovná:

X_B = n_B / (n^L + n^Vložka)

Kde n_B Sú to celkové móly B vo fáze kvapaliny aj pary, a n^L a n^Vložka sú príslušné móly pre tieto fázy. Vyčistenie n_B budeme mať:

n_B = X_Bn^L + X_Bn^Vložka (1)

Na druhej strane, n_B Tiež sa rovná:

n_B = n_B^L + n_B^Vložka

= X_B^Ln^L + X_B^Vložkan^Vložka  (2)

Teraz vyrovnanie rovníc (1) a (2) nám poskytne:

X_Bn^L + X_Bn^Vložka = X_B^Ln^L + X_B^Vložkan^Vložka

A usporiadať:

n^L(X_B - X_B^L) = n^Vložka(X_B^Vložka - X_B) (3)

n^L(C-d) = n^Vložka(Z)

Tieto posledné dva matematické výrazy sú pravidlom páky. Všimnite si, že x_B - X_B^L Je to vzdialenosť medzi bodmi C a D; a x_B^Vložka - X_B, Je to vzdialenosť medzi bodmi D-E: dve polovice väzbovej čiary (pákové ramená).

Táto rovnica je veľmi podobná rovnomernej rovnováhe mas na rockeri s Fulcro:

m₁l₁ = m₂l₂

Pravidlo páky nám teda umožní vypočítať celkové móly n^L a n^Vložka za predpokladu, že sú známe celkové móly zmesi, n_Tón (n_Tón = n^L + n^Vložka).

Druhá forma

Predchádzajúci výraz pre pravidlo páky slúži na výpočet množstiev (hmotnosti, móly atď.) fáz v rovnováhe. Najznámejšia verzia pravidla páky nám však umožňuje vypočítať frakcie alebo percentuálne podiely každej fázy, pričom medzi x berie iba vzdialenosti medzi x_B, X_B^L a x_B^Vložka.

Zoberme si rovnaký systém vyššie, ktorý máte inú formu pravidla páky:

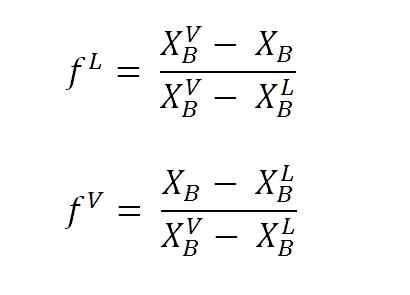Rovnice na výpočet kvapalinových a parných frakcií pomocou páky ramien. Zdroj: Gabriel Bolívar.

Kde F ^L a F ^VložkaSú to molárne frakcie (alebo percento, v závislosti od grafu) fáz kvapaliny a pary. Všimnite si, že, samozrejme, F ^L a F ^Vložka Nemajú žiadne jednotky; zatiaľ čo n^L a n^Vložka Áno, majú jednotky (móly, gramy atď.).

Môže vám slúžiť: reakčné teplo

Príklady

Spôsob 1

V nádobe 28 mólov B a 12 mólov A sú zmiešané. Stanovte množstvá a molárne frakcie pre vytvorené fázy.

Vypočítame x_B:

X_B = (28 molov B)/ (28 molov B + 12 molov A)

= 0.7

Táto hodnota zodpovedá x_B horného diagramu. Odpočúvanie nám poskytne približne nasledujúce hodnoty pre x_B^L a x_B^Vložka:

X_B^L = 0.41

X_B^Vložka = 0.94

S pravidlom páky:

n^L(X_B - X_B^L) = n^Vložka(X_B^Vložka - X_B)

A vedieť to n_Tón = n^L + n^Vložka, a? n_Tón = 40 mólov, potom vyčistíme n^L ani n^Vložka v závislosti od druhého:

n^L(X_B - X_B^L) = (40 mólov - n^L) (X_B^Vložka - X_B)

Usporiadanie a čistenie n^L budeme mať:

n^L = (40 mólov) (x_B^Vložka - X_B) / (X_B^Vložka - X_B^L)

Nepamätá si tento výraz F ^L? Teraz nahradenie, budeme mať:

n^L = (40 molov) (0.94 - 0.70) / (0.94 - 0.41)

= 18.11 mólov v kvapalnej fáze

Môžeme vypočítať n^Vložka Dvoma spôsobmi:

n^Vložka = n^L(X_B - X_B^L) / (X_B^Vložka - X_B)

ani

n^Vložka = 40 molov - 18.11 mólov

= 21.89 krtkov v parnej fáze

Metóda 2

Čo keď najskôr vypočítame F ^L a F ^Vložka?

F ^L = (X_B^Vložka - X_B) / (X_B^Vložka - X_B^L)

= (0.94 - 0.70) / (0.94 - 0.41)

= 0.4528 alebo 45.28%

To znamená, 45.2% mólov je v kvapalnej fáze, čo je množstvo rovné:

n^L = F ^Ln_Tón

= (0.4528) (40 mólov)

= 18.11 mólov

A F ^Vložka Môžeme to vypočítať rovnako dvoma spôsobmi:

F ^Vložka = 1 - F ^L

ani

F ^Vložka = (X_B - X_B^L) / (X_B^Vložka - X_B^L)

Byť jej hodnotou:

F ^Vložka = 0.5472 alebo 54.72%

A preto, n^Vložka Bude to rovnaké:

n^Vložka = F ^Vložkan_Tón

= (0.5472) (40 mólov)

= 21.89 mólov

Všimnite si, že použitie dvoch foriem pravidla páky ako metódy alternatívneho výpočtu je možné dosiahnuť rovnaké výsledky. Metóda 2 sa zdá byť priamejšia a jednodulnejšia; Ale ak sa pozorne pozoruje, po vyriešení zúčtovania n^L ani n^Vložka, Zistí sa, že obe metódy sú v skutočnosti rovnako ľahké.

Vyriešené cvičenia

Ďalej sa vyriešia ďalšie dve cvičenia, kde sa zvážené systémy budú vyžadovať kvapalinové a nekrižadlové vapor. Schémy sú tiež grafické vzhľadom na teplotu systému a nie ich tlak.

Cvičenie 1

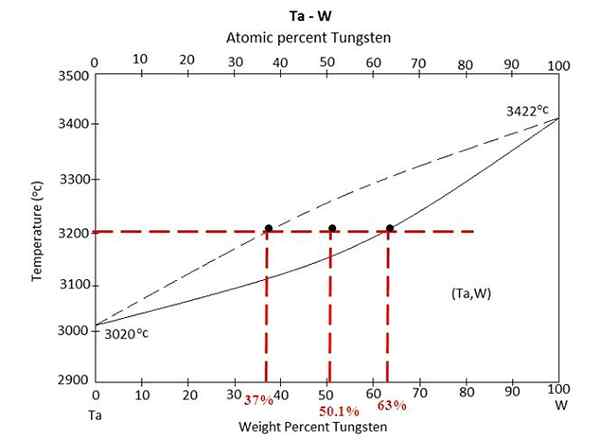Fázový diagram pre zliatinu medzi Tantalo a volfrámom. Zdroj: Materialdia, CC BY-SA 4.0, cez Wikimedia Commons

Máme fázový diagram nad zliatinou medzi Tantalo a volfrámom, TA-W. Na osi x je znázornené globálne hmotnostné percentá volfrámu, W% (m/m).

V rámci kvapalinovej rovnovážnej oblasti (TA+W) a tuhej látky (zliatiny) je zmes pri 3200 ° C. Stanovte hmotnosti každej fázy za predpokladu, že sa zahrieva 100 gramov zliatiny.

Môže vám slúžiť: kovy, nemetály a metaloidy

Postup

Tentoraz sa cvičenie vyrieši pomocou druhej formy pravidla páky. Linka Únie nám hovorí, že: V pevnej fáze máme 63% volfrámu, zatiaľ čo v kvapalnej fáze máme 37% volfrámu. Dôvodom je, že volfrám sa topí na vyššiu teplotu (3422 ° C) ako tantal (3020 ° C).

Takže máme:

W%^Siež alebo w_Siež= 63%

W%^L alebo w_L= 37%

A tiež:

W₀ = 50.1%

Uplatňujeme pravidlo páky na F ^L:

F ^L = (63% - 50.1%) / (63% - 37%)

= 0.4961 alebo 49.61%

Všimnite si, že vzdialenosť zodpovedajúca kvapalnej fáze je rameno páky v blízkosti pevnej fázy, opačná strana stredného bodu.

Hmotnosť kvapalnej fázy je preto:

(0.4961) (100 gramov) = 49.61 roztavených gramov

A pevná fáza sa bude rovnať:

100 gramov - 49.61 gramov = 50.39 gramov zliatiny bohatých na volfrámu

Cvičenie 2

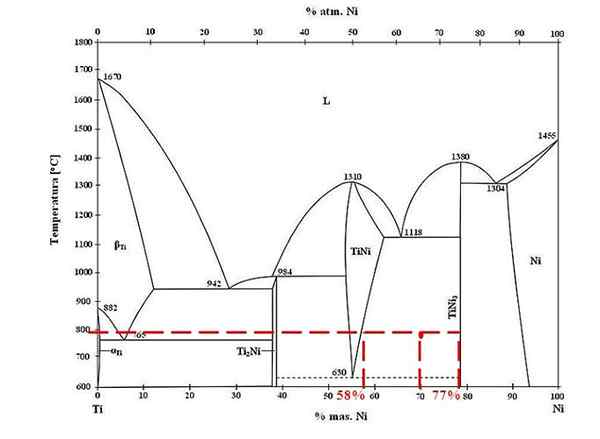Fázový diagram pre zliatiny titánových a-a-zliatiny. Zdroj: Doomgiver, CC By-SA 3.0, cez Wikimedia Commons

Pre zliatinu titánu a niklu pri 800 ° C a so 70% niklu určte, koľko z Tini a Tini₃ Sú prítomní.

Postup

Tentoraz žiadajú iba hromadné frakcie každej fázy. Červený bod je umiestnený v rovnovážnej oblasti medzi fázami TINI a TINI₃, ktorých krivky sú tam, kde hrá líniu Únie, ktorá tečie k hodnotám 58% alebo pre fázu TINI a 77% alebo pre fázu TINI₃.

Všimnite si, že červený bod je bližšie k fáze Tini₃ fáza Tini. To znamená, že musí byť viac Tini₃ že tini; A preto vzdialenosť alebo rameno páky zodpovedajúce TINI₃ Musí to byť najdlhší, naopak (70%-58%).

Vedieť to, pokračujeme vo výpočte F ^Tini3:

F ^Tini3 = (70% - 58%) / (77% - 58%)

= 0.6316 alebo 63.16%

Naozaj, 63.16% zliatiny zodpovedá fáze Tini₃. Medzitým fáza TINI zodpovedá:

1 = F ^Tini3 + F ^Tini

F ^Tini = 1 - F ^Tini3

= 0.3684 alebo 36.84%

Záverom z vzniku cvičení môžeme povedať, že pravidlo páky je veľmi užitočné na určenie frakcií každej fázy v rovnováhe pre systém dvoch komponentov.

Odkazy

1. Walter J. Moore. (1963). Fyzikálna chémia. V chemickej kinetike. Štvrté vydanie, Longmans.
2. Irán. Levine. (2009). Princípy fyzikálneho spôsobu. Šieste vydanie. MC Graw Hill.
3. Wikipedia. (2020). Pravidlo páky. Zdroj: In.Wikipedia.orgán
4. Michael Adewumi. (18. mája 2020). Pravidlo páky. Získané z: Eng.Librettexts.orgán
5. Adam Warren. (1997). Fázové diagramy: kravaty a pravidlo páky. Získané z: Southampton.Ac.Uk
6. University of Cambridge. (2020). Pravidlo páky. Zdroj: doitpoms.Ac.Uk