Pravá ruka

postava 1. Pravá ruka. Zdroj: Wikimedia Commons. ACDX [CC BY-S (http: // creativeCommons.Org/licencie/By-SA/3.0/]].

Aké je pravidlo pravej ruky?

Ten pravá ruka Je to mnemotechnický zdroj na stanovenie smeru a smeru vektora v dôsledku vektorového produktu alebo krížového produktu. Vo všeobecnosti sa používa vo fyzike, pretože existujú dôležité vektorové veľkosti, ktoré sú výsledkom vektorového produktu. To je napríklad krútiaci moment, magnetická sila, uhlová hybnosť a magnetický moment.

Byť dvoma všeobecnými vektormi do a b ktorého krížový produkt je do X b. Modul takého vektora je:

do X b = do.b.hriech α

Kde a je minimálny uhol medzi do a b, Zatiaľ čo A a B predstavujú ich moduly. Na rozlíšenie vektorov od ich modulov sa používajú výrazné písmená.

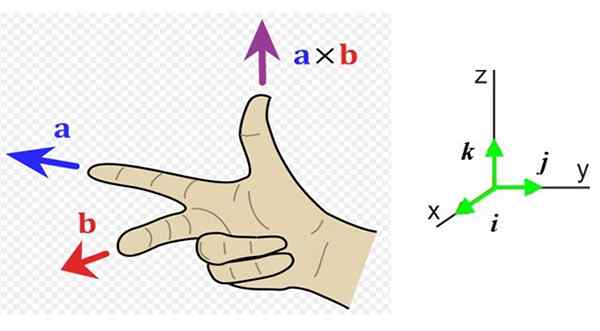
Teraz potrebujeme poznať smer a význam tohto vektora, takže je vhodné mať referenčný systém s tromi smermi priestoru (obrázok 1 vpravo). Jednotkové vektory Jo, J a klimatizovať Ukazujú na čitateľa (mimo stránky), doprava a nahor.

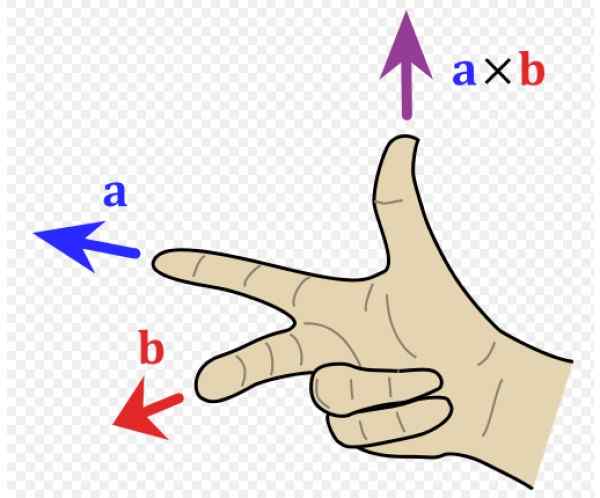
V príklade na obrázku 1 vľavo vektor do smeruje doľava (adresa a záporný a ukazovák pravej ruky) a vektor b ide do čitateľa (adresa X Pozitívny, prostredný prst pravej ruky).

Výsledný vektor do X b Má smer palec, smerom hore v smere z pozitívny.

Druhé pravidlo pravej ruky

Toto pravidlo sa používa veľa, keď existujú veľkosti, ktorých smer a význam sa rotujú, napríklad magnetické pole B produkovaný tenkým a priamym drôtom, ktorý prepravuje prúd.

V tomto prípade sú riadky magnetického poľa sústredné obvody s drôtom a smer odbočenia sa získa týmto pravidlom takto: pravý palec označuje smer prúdu a zostávajúce štyri prsty sú zakrivené v smere smerom k smeru smer poľa. Koncept ilustrujeme na obrázku 2.

Môže vám slúžiť: elastické otrasy: v rozmere, špeciálne prípady, cvičenia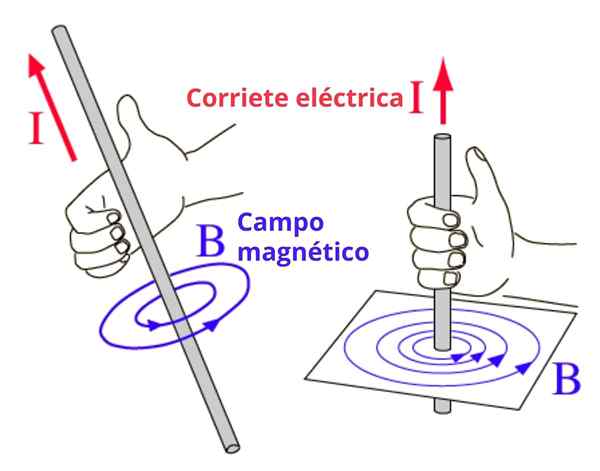Obrázok 2. Pravá ruka na určenie významu obehu magnetického poľa

Alternatívne pravidlo pravej ruky

Nasledujúci obrázok ukazuje alternatívnu formu pravidla pravého ruky. Vektory, ktoré sa objavujú v osvietení, sú:

• Rýchlosť vložka presného zaťaženia.
• Magnetické pole B v rámci ktorého sa zaťaženie pohybuje.
• F_B Sila, ktorú magnetické pole vyvíja na zaťaženie.

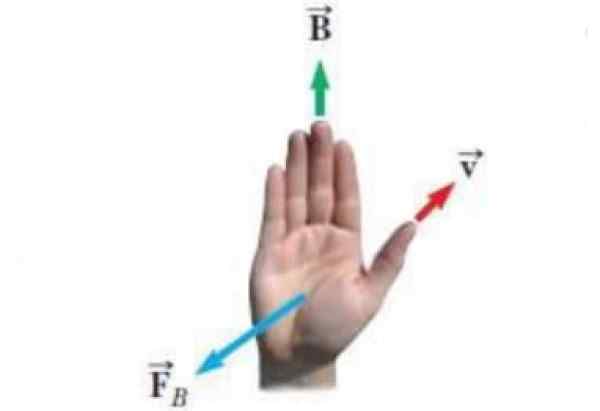Obrázok 3. Alternatívne pravidlo pravej ruky. Zdroj: Wikimedia Commons. Expertikuis [CC BY-SA (https: // creativeCommons.Org/licencie/By-SA/4.0)]

Rovnica magnetickej sily je F_B = qvložka X B a pravidlo pravej ruky poznať smer a zmysel pre F_B Platí to takto: palec body podľa V, zostávajúce štyri prsty sú umiestnené podľa poľa B. Tak F_B Je to vektor, ktorý vychádza z dlane ruky, kolmo na ňu, akoby tlačil zaťaženie.

Poznač si to F_B ukázalo by sa opačným smerom, ak by zaťaženie, ktoré bolo negatívne, pretože vektorový produkt nie je komutatívny. V skutočnosti:

do X B = - B X do

Žiadosti

Pravidlo pravej ruky sa dá aplikovať na rôzne fyzikálne veľkosti, povedzme niektoré z nich:

Uhlová rýchlosť a zrýchlenie

Obe uhlová rýchlosť Ω Ako uhlové zrýchlenie α Sú to vektory. Ak sa objekt otáča okolo pevnej osi, je možné uhlovú rýchlosť Ω.

Z hľadiska uhlového zrýchlenia α bude mať rovnakú adresu ako Ω, Ale jeho význam závisí od IF Ω Zvyšuje alebo znižuje jeho veľkosť v priebehu času. V prvom prípade majú obe rovnaký smer a význam, ale v druhom bude mať opačné zmysly.

Môže vám slúžiť: Watt Law: Čo je, príklady, aplikácie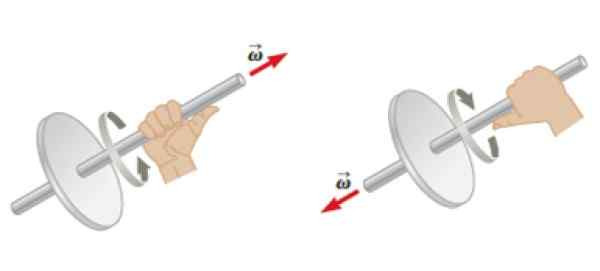Obrázok 4. Pravidlo pravej ruky aplikované na objekt v rotácii na určenie smeru a smeru uhlovej rýchlosti. Zdroj: Serway, r. Fyzický.

Uhlová hybnosť

Uhlový vektor L_Ani častice, ktorá sa otáča okolo určitej osi alebo je definovaná ako vektorový produkt svojho vektora okamžitej polohy r  a množstvo lineárneho pohybu p:

L = r X p

Pravidlo pravice sa používa týmto spôsobom: ukazovák je umiestnený v rovnakom smere a smere r, Prostredný prst v p, Obaja na vodorovnej rovine, ako na obrázku. Automaticky sa palec rozširuje vertikálne smerom nahor a ukazuje smer smeru a smeru uhlovej hybnosti L_Ani.

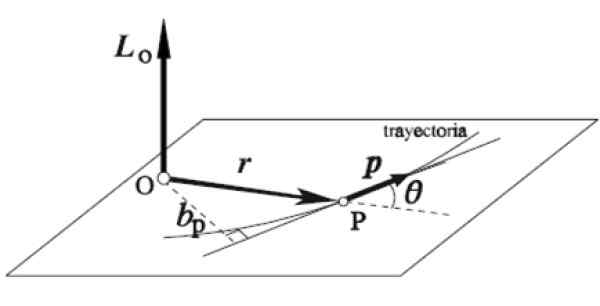Obrázok 5. Uhlový vektor. Zdroj: Wikimedia Commons.

Cvičenia

Cvičenie 1

Rotácie na obrázku 6 prebieha rýchlo s uhlovou rýchlosťou Ω a jej os symetrie rozbitejšie pomalšie okolo vertikálnej osi z. Tento pohyb sa volá precesia. Opíšte sily, ktoré pôsobia na točenie a účinok, ktorý vytvárajú.

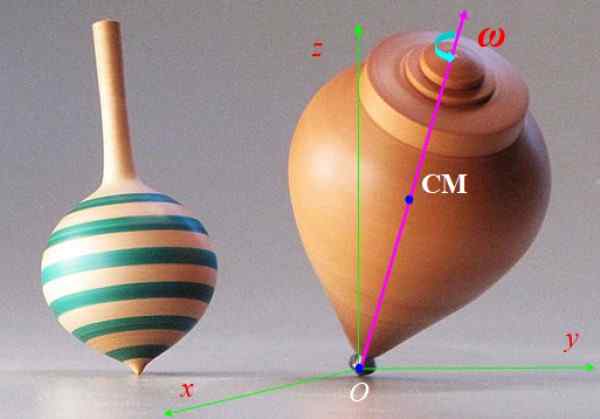Obrázok 6. Točenie. Zdroj: Wikimedia Commons.

Riešenie

Sily pôsobiace na rotáciu sú normálne N, aplikované na podporný bod so zemou alebo viac hmotnosťou mg, aplikované v strede hmotnosti cm, s g Vektor zrýchlenia závažnosti, smerovaný vertikálne nadol (pozri obrázok 7).

Obe sily sú vyvážené, preto sa točenie nepohybuje. Hmotnosť však vytvára krútiaci moment alebo krútiaci moment τ Sieť o bode alebo, dané:

τ_Ani = r_Ani X F, s F = Mg.

Ako r a mg Sú vždy v lietadle, keď sa otáčanie otáča, podľa pravidla pravej ruky krútiaci moment τ_Ani Vždy sa nachádza v lietadle Xy, kolmé obidve a r ako g.

Poznač si to N nevyrába krútiaci moment vzhľadom na O, pretože jeho vektor r Pokiaľ ide o alebo je null. Tento krútiaci moment vytvára zmenu uhlovej hybnosti, ktorá spôsobuje precesiu rotácie okolo osi Z.

Môže vám slúžiť: termodynamická rovnováha: triedy a aplikácie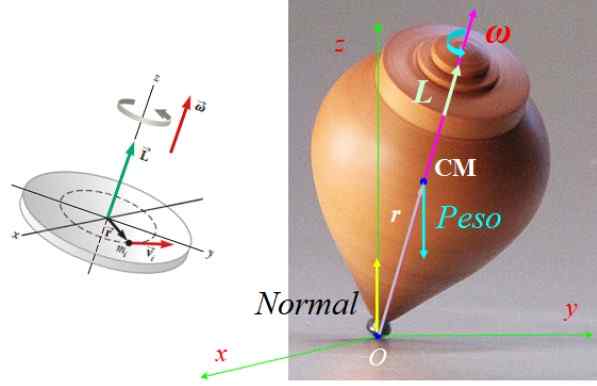Obrázok 7. Sily pôsobiace na rotáciu a jeho vektor uhlovej hybnosti. Zdroj ľavého obrázku: Serway, r. Fyzika pre vedu a inžinierstvo.

Cvičenie 2

Ukazujte smer a smer vektora uhlovej hybnosti L z trumpe na obrázku 6.

Riešenie

Akýkoľvek bod rotácie má hmotnosť m_Jo, rýchlosť vložka_Jo a vektor polohy r_Jo, Keď sa točí okolo osi Z. Uhlová hybnosť L_Jo z uvedených častíc je:

L_Jo = r_Jo X p_Jo = r_Jo x m_Jovložka_Jo

Vzhľad r_Jo a vložka_Jo Sú kolmé, veľkosť L je:

L_Jo = m_Jor_Jovložka_Jo

Lineárna rýchlosť vložka súvisí s uhlovou rýchlosťou Ω cez:

vložka_Jo = r_JoΩ

Preto:

L_Jo = m_Jor_Jo (r_JoΩ) = m_Jor_Jo²Ω

Celková uhlová hybnosť trompo l je súčtom uhlovej hybnosti každej častice:

L = (∑m_Jor_Jo² ) Ω

∑ m_Jor_Jo²  Je to moment zotrvačnosti i točenia, potom:

L= IΩ

Preto L a Ω Majú rovnaký smer a význam, ako je znázornené na obrázku 7.