Zníženie podobných výrazov

Aké je zníženie podobných výrazov?

Ten Zníženie podobných výrazov Je to metóda použitá na zjednodušenie algebraických výrazov. V algebraickom výraze sú podobné pojmy, ktoré majú rovnakú premennú; to znamená, že majú rovnaké neznáme reprezentované listom a majú rovnaké exponenty.

V niektorých prípadoch sú polynómy rozsiahle a aby ste dosiahli riešenie, musíte sa pokúsiť znížiť výraz; To je možné, keď existujú výrazy, ktoré sú podobné, ktoré sa dajú kombinovať pomocou algebraických operácií a vlastností, ako je súčet, odčítanie, násobenie a delenie.

Vysvetlenie

Podobné výrazy sú tvorené rovnakými premennými s rovnakými exponentmi av niektorých prípadoch sa líšia iba podľa ich numerických koeficientov.

Tí, ktorí nemajú žiadne premenné, sa tiež považujú za podobné pojmy; to znamená, že podmienky, ktoré majú iba konštanty. Napríklad napríklad sú podobné pojmy:

• 6x² - 3x². Obe výrazy majú rovnakú premennú x².
• 4²b³ + Druhý²b³. Oba výrazy majú rovnaké premenné²b³.
• 7 - 6. Podmienky sú konštantné.

Tieto výrazy, ktoré majú rovnaké premenné, ale s rôznymi exponentmi sa nazývajú nepodstatné výrazy, napríklad:

• 9²B + 5AB. Premenné majú rôzne exponenty.
• 5x + a. Premenné sú rôzne.
• B - 8. Jeden výraz má premennú, druhý je konštanta.

Identifikácia podobných výrazov, ktoré tvoria polynóm, sa dajú zredukovať na jeden a kombinovať všetkých tých, ktorí majú rovnaké premenné s rovnakými exponentmi. Týmto spôsobom je výraz zjednodušený znížením počtu výrazov, ktoré ho zostavujú, a výpočet jeho roztoku je uľahčený.

Ako urobiť zníženie podobných výrazov?

Zníženie podobných podmienok sa vykonáva uplatňovaním asociatívneho vlastníctva sčítania a distribučného vlastníctva produktu. Pri použití nasledujúceho postupu je možné znížiť podmienky:

• Po prvé, podobné pojmy sú zoskupené spolu.
• Koeficienty (čísla, ktoré sprevádzajú premenné) podobných pojmov, sa pridávajú alebo odpočítajú a uplatňujú sa asociatívne, komutatívne alebo distribučné vlastnosti, ako sa to môže.
• Potom sú napísané nové získané výrazy, ktoré pred nimi umiestnia znamenie, ktoré vyplynulo z operácie.

Môže vám slúžiť: diskrétna matematika

Príklad

Znížte podmienky nasledujúceho výrazu: 10x + 3y + 4x + 5y.

Riešenie

Najprv sú podmienky nariadené tak, aby zoskupili tie, ktoré sú podobné, uplatňujúca komutatívnu nehnuteľnosť:

10x + 3y + 4x + 5y = 10x + 4x + 3y + 5y.

Potom sa použije distribučná vlastnosť a koeficienty, ktoré sprevádzajú premenné, sa pridajú, aby sa dosiahli zníženie podmienok:

10x + 4x + 3y + 5y

= (10 + 4) x + (3 + 5) a

= 14x + 8y.

Na zníženie podobných výrazov je dôležité vziať do úvahy príznaky, ktoré majú koeficienty, ktoré sprevádzajú premennú. Existujú tri možné prípady:

Zníženie podobných výrazov s rovnakými príznakmi

V tomto prípade sa pridávajú koeficienty a pred výsledkom sa známka podmienok umiestni. Preto, ak sú pozitívne, výsledné pojmy budú pozitívne; V prípade, že sú podmienky negatívne, výsledok bude mať znamenie (-) sprevádzané premennou. Napríklad:

a) 22Ab² + 12Ab² = 34 AB².

b) -18x³ - 9x³ - 6 = -27x³ - 6.

Zníženie podobných výrazov CNa rôznych príznakoch

V tomto prípade sa koeficienty odpočítajú a pred výsledkom sa umiestni znak hlavného koeficientu. Napríklad:

a) 15x²a - 4x²a + 6x²a - 11x²a

= (15x²a + 6x²Y) + ( - 4x²a - 11x²a)

= 21x²Y + (-15x²a)

= 21x²a - 15x²a

= 6x²a.

b) -5a³B + 3 a³B - 4a³B + a³b

= (3 a³B + a³b) + (-5a³B - 4a³b)

= 4a³B - 9a³b

= -5 a³b.

Týmto spôsobom sa na zníženie podobných výrazov, ktoré majú rôzne príznaky, sa vytvára jediný aditívny termín so všetkými tými, ktoré majú kladné znamenie (+), pridávajú sa koeficienty a výsledok je sprevádzaný premennými.

Môže vám slúžiť: Unitárny kruh: trigonometrické funkcie a aplikácie

Rovnakým spôsobom sa vytvára subtraktívny termín, so všetkými podmienkami, ktoré majú negatívny znak (-), sa pridávajú koeficienty a výsledok je sprevádzaný premennými.

Nakoniec sa odpočítajú sumy dvoch tvorených výrazov a znak najväčšieho je uvedený na výsledok.

Zníženie podobných výrazov v operáciách

Zníženie podobných pojmov je operácia algebry, ktorá sa dá uplatniť v súčtu, odčítaní, násobení a algebraickom delení.

Sumy

Ak máte niekoľko polynómov s podobnými výrazmi, na ich zníženie, podmienky každého polynómu sa nariadia, aby si udržali svoje znamenia, potom sú napísané za ostatnými a podobné výrazy sú znížené. Napríklad máte nasledujúce polynómy:

3x - 4xy + 7x²a + 5xy².

- 6x²a - 2xy + 9 xy² - 8x.

V odčítaniach

Aby sa odpočítal polynóm od iného, ​​píše sa Minuend a potom ho odpočítava svojimi zmenenými znakmi a potom sa urobí zníženie podobných výrazov. Napríklad:

5³ - 3Ab² + 3B²c

6Ab² + Druhý³ - 8b²c

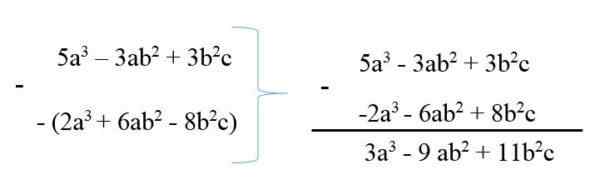
Polynómy sú teda zhrnuté na 3A³ - 9ABAB² + 11b²c.

Pri násobení

V polynómovom produkte sú výrazy, ktoré tvoria vynásobenie pre každý výraz, ktorý tvorí multiplikátor, vzhľadom na to, že príznaky násobenia zostávajú rovnaké, ak sú pozitívne, ak sú pozitívne.

Zmenia sa iba vtedy, keď sa vynásobia výrazom, ktorý je negatívny; To znamená, že keď dva výrazy toho istého znaku vynásobia výsledok, bude pozitívny (+) a keď budú mať rôzne príznaky, výsledok bude záporný (-).

Napríklad:

a) (a + b) _* (A + b)

= a² + AB + AB + B²

= a² + 2ab+ b².

b) (a + b) _* (A - b)

= a² - AB + AB - B²

= a² - b².

taxík) _* (A - b)

= a² - AB - AB + B²

= a² - 2ab+ b².

V divíziách

Ak chcete znížiť dva polynómy prostredníctvom divízie, musí tretí polynóm.

Môže vám slúžiť: Tukey Test: Čo je v prípade príkladu vyriešené cvičenie

Z tohto dôvodu musia byť podmienky dividend a deliteľa nariadené, zľava doprava, takže premenné sú v rovnakom poradí.

Divízia sa potom vykonáva, počnúc od prvého funkčného obdobia zľava dividend medzi prvou vľavo od deliča, vždy berúc do úvahy príznaky každého funkčného obdobia.

Napríklad znížte polynóm: 10x⁴ - 48x³a + 51x²a² + 4xy³ - 15 rokov⁴ Rozdelenie medzi polynómom: -5x² + 4xy + 3y².

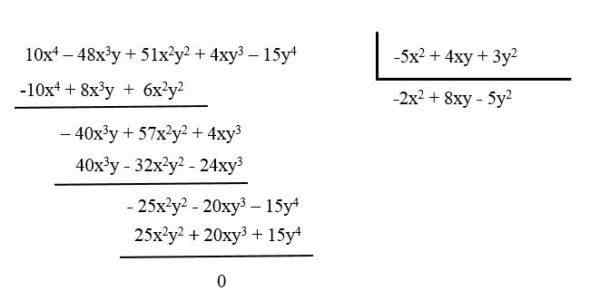
Výsledný polynóm je -2x² + 8xy - 5y².

Vyriešené cvičenia

Prvé cvičenie

Znížte podmienky daného algebraického výrazu:

15a² - 8Ab + 6a² - 6AB - 9 +4A² - 13 ab.

Riešenie

Uplatňuje sa komutatívna vlastnosť sumy a zoskupuje podmienky, ktoré majú rovnaké premenné:

15a² - 8Ab + 6a² - 6AB + 9 + 4A² - 13

= (15a² + 6² + 4²) + ( - 8AB - 6AB) + (9 - 13).

Potom sa použije distribučná vlastnosť násobenia:

15a² - 8Ab + 6a² - 6AB + 9 + 4A² - 13

= (15 + 6 + 4) a² + ( - 8 - 6) AB + (9 - 13).

Nakoniec sú zjednodušené pridaním a odpočítaním koeficientov každého pojmu:

15a² - 8Ab + 6a² - 6AB + 9 + 4A² - 13

= 25A² - 14AB - 4.

Druhé cvičenie

Zjednodušte produkt nasledujúcich polynómov:

(8x³ + 7xy²)_*(8x³ - 7 xy²).

Riešenie

Každý termín prvého polynómu sa vynásobí druhým, berúc do úvahy, že znaky podmienok sú rôzne; Výsledok jeho násobenia bude preto negatívny, ako aj zákony exponentov sa musia uplatniť.

(8x³ + 7xy²) _* (8x³ - 7xy²)

= 64 x⁶ - 56 x³_* Xy² + 56 x³_* Xy² - 49 x²a⁴

= 64 x⁶ - 49 x²a⁴.