Koncept, charakteristiky, príklady, cvičenia Bravais siete

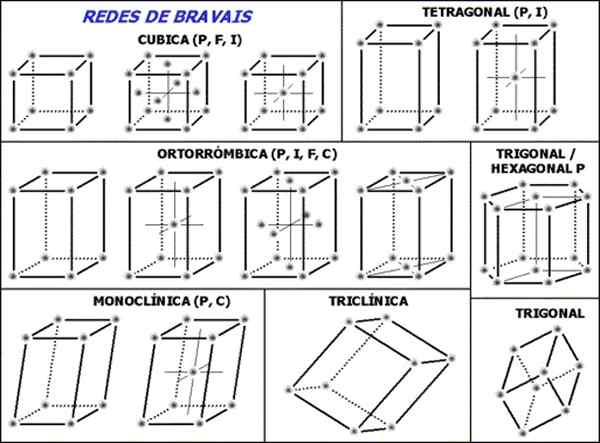
Ten Siete Sú to sada štrnástich troch rozmerových jednotkových buniek, v ktorých atómy kryštálu. Tieto bunky pozostávajú z trojrozmerného usporiadania bodov, ktoré tvoria základnú štruktúru, ktorá sa pravidelne opakuje v troch priestorových smeroch.

Pôvod tejto nominálnej hodnoty pre základné kryštalické štruktúry pochádza z roku 1850, keď Auguste Bravais ukázal, že je možných iba 14 možných základných trojrozmerných jednotiek.

postava 1. Siete Bravais sú sada 14 nevyhnutných a dostatočných jednotkových buniek na opis akejkoľvek kryštalickej štruktúry. (Wikimedia Commons)

Sada 14 sietí Bravais je rozdelená do siedmich skupín alebo štruktúr podľa geometrie buniek, týchto sedem skupín je:

1- kubický

2- tetragonálny

3- ortorrombický

4- trigonal-hexagonálny

5- monoklinický

6- triklinický

7-trigonálny

Každá z týchto štruktúr definuje jednotnú bunku, ktorá je najmenšou časťou, ktorá si zachováva geometrické usporiadanie atómov v skle.

[TOC]

Charakteristiky sietí Bravais

Štrnásť sietí Bravais, ako je uvedené vyššie, sú rozdelené do siedmich skupín. Ale každá z týchto skupín má svoje jednotkové bunky s charakteristickými parametrami, ktoré sú:

1- Sieťový parameter (A, B, C)

2- počet atómov na bunku

3- Vzťah medzi sieťovými parametrami a atómovým rádiom

4-koordinačné číslo

5-balenie faktor

6- Intersticiálne priestory

7- Translaciami pozdĺž vektorov A, B, C sa kryštalická štruktúra opakuje.

Kubické siete

Skladá sa z jednoduchej alebo kubickej kubickej siete, kubickej siete zameranej na tváre alebo kubickú sieť F a kubickú sieť zameranú na kubické telo alebo sieť.

Všetky kubické siete majú tri tri Parametre siete zodpovedá adresám X, Y, z rovnakej hodnoty:

A = b = c

Kubická sieť P

Je vhodné zdôrazniť, že atómy sú reprezentované guľami, ktorých centrá sú vo vrcholoch kubickej bunky P.

Môže vám slúžiť: umelé satelity

V prípade kubickej siete P počet atómov na bunku Je to 1, pretože v každom vrchole je iba ôsma časť atómu vo vnútri jednotkovej bunky, potom 8*⅛ = 1.

On Koordinačné číslo Označuje počet atómov, ktoré sú v blízkosti susedov v kryštalickej sieti. V prípade kubickej siete p je koordinačné číslo 6.

Kubická sieť i

V tomto type siete Okrem atómov vo vrcholoch kocky sa nachádza atóm v strede kocky. Tak číslo atómu na bunku Jednotný v kubickej sieti p je 2 atómy.

Obrázok 2. Kubická sieť zameraná na telo.

Kubická sieť f

Je to kubická sieť, ktorá má okrem atómov vo vrcholoch atóm v strede tváre každej kocky. On počet atómov na bunku Je to 4, pretože každý zo šiestich atómov tváre má polovicu vo vnútri bunky, hovorí 6*½ = 3 plus 8*⅛ = 1 vo vrcholoch.

Obrázok 3. Kubická sieť zameraná na tváre.

Hexagonálna sieť

V tomto prípade je jednotková bunka priamy šesťuholníkový hranol. Hexagonálne siete majú tri tri Parametre siete zodpovedajúce splnenie nasledujúceho vzťahu:

A = b ≠ c

Je uhol medzi vektorom A a B 120 °, ako je znázornené na obrázku. Zatiaľ čo medzi vektormi A a C, ako aj medzi B a C sú priame uhly.

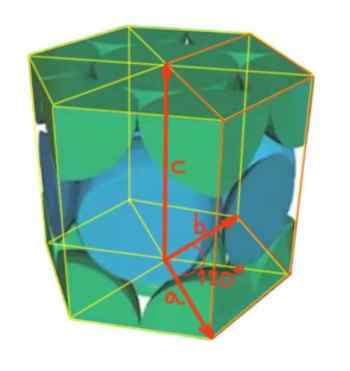Obrázok 4. Hexagonálna sieť.

On počet atómov na bunku Bude sa vypočítavať takto:

- V každej z 2 báz šesťuholníkového hranolu je v šiestich vrcholoch 6 atómov. Každý z týchto atómov zaberá ⅙ jednotnej bunky.

- V strede každej z 2 šesťuholníkových základov je 1 atóm, ktorý zaberá 1/2 jednotnej bunky.

- Na 6 bočných tvárach hexagonálneho hranolu sú 3 atómy, z ktorých každý zaberá ⅔ jednotkovej bunky a 3 atómy, ktoré zaberajú každý ⅓ objemu jednotkovej bunky.

Môže vám slúžiť: Počuť silu: povrchové a hmotnostné sily

(6 x ⅙) x 2 + ½ x 2 + ⅔ x 3 + ⅓ x 3 = 6 

Vzťah medzi parametrami siete A a B s atómovým polomerom R sa za predpokladu, že všetky atómy sú rovnakého rádu a sú v kontakte, je: 

a/r = b/r = 2

Príklady

Kovy sú hlavnými príkladmi kryštalických štruktúr a tiež najjednoduchšie, pretože všeobecne pozostávajú z jedného typu atómu. Existujú však aj iné nemetalické zlúčeniny, ktoré tiež tvoria kryštalické štruktúry, ako je diamant, kremeň a mnoho ďalších.

- Železo

Železo má jednoduchú bunku kubickej jednotky s parametrom siete alebo okrajom A = 0,297 nm. V 1 mm existujú bunky 3,48 x 10^6 jednotiek.

- Meď

Má kubickú kryštalickú štruktúru sústredenú na tvári, tvorenú iba atómami medi.

- Drahokamy

Drahé drahokamy sú kryštalické štruktúry v podstate rovnaká zlúčenina, ale s malými časťami nečistôt, ktoré sú často zodpovedné za ich farbu.

diamant

Je zložený iba z uhlíka a neobsahuje nečistoty, a preto nemá farbu. Diamant má Kubická kryštalická štruktúra (izometrický hexoktahedrál) a je najťažším známym materiálom.

Štrbina

Skladá sa z oxidu oxidu kremičitého, zvyčajne je bezfarebný alebo biely. Jeho kryštalická štruktúra je trigonálna-Trapezoédrica.

Rubínový 

Skladá sa z oxidu hlinitého s chrómovými nečistotami, ktoré mu dodávajú jeho charakteristickú červenú farbu. Tvorí jeden Hexagonálna kryštalická sieť.

Zafír 

Je to tiež kryštál oxidu hliníka, ale s nečistotami titánu a železa, ktoré sú zodpovedné za svoju modrú farbu v rôznych odtieňoch. Ako Ruby má hexagonálna štruktúra.

Jadro

Drahý kameň všeobecne zelený, má Monoklinická štruktúra A je zložený z kremičitanu železa-magnézium-calcio.

Topaz 

Je bezfarebný s a Ortorrombická štruktúra fluoridu hliníka hydroxidu.

Vyriešené cvičenia

Cvičenie 1

Nájdite vzťah medzi parametrom siete a atómovým polomerom pre kubickú sieť f.

Môže vám slúžiť: Teória veľkého tresku: Charakteristiky, fázy, dôkazy, problémy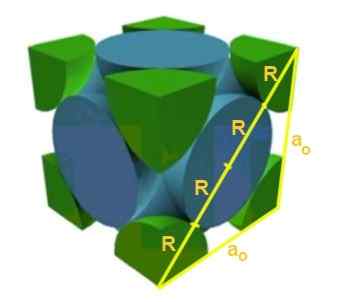

Riešenie: V prvom rade sa predpokladá, že atómy sú znázornené ako gule všetky polomer R v „kontakte“ medzi sebou, ako je znázornené na obrázku. Vytvára sa obdĺžnikový trojuholník, v ktorom sa splní:

(4 r)^2 = a^2 + a^2 = 2 a^2

Takže máte, že vzťah Edge-Radio je:

A/r = 4/√2

Cvičenie 2

Nájdite vzťah medzi parametrom siete a atómovým polomerom pre kubickú sieť I (zameraný na telo).

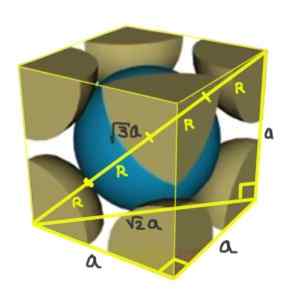
Riešenie: Atómy majú byť reprezentované ako všetky guľové gule v „kontakte“, ako je to znázornené na obrázku.

Dva obdĺžniky sú tvorené jedným z hypotenusa √2a a druhého z hypotenus √3a, ako sa dá preukázať pomocou Pythagorovej vety. Odtiaľ musíte vzťah medzi sieťovým parametrom a atómovým polomerom pre kubickú sieť I (sústredené v tele) je:

A/r = 4/√3

Cvičenie 3

Nájdite baliaci faktor F pre jednotkovú bunku kubickej štruktúry F (kubický sústredený na tváre), v ktorom majú atómy rádio R a sú v „kontakte“.

Riešenie: Baliaci faktor F je definovaný ako pomer medzi objemom obsadeným atómami v jednotkovej bunke a objemom bunky:

F = vatómy / Vbunka

Ako je uvedené vyššie, počet atómov na jednotku bunky kubickej siete zameranej na tváre je 4, takže balenie bude:

F = 4 [4πr^3/3] /[a^3] =…

… 4 [4πr^3/3]/[4R/√2]^3 = (√2) π/6 = 0,74

Odkazy

1. Centrum akademických zdrojov krištáľových štruktúr. [PDF]. Získané 24. mája 2018, z: Web.iIT.Edu
2. Kryštály. Získané 26. mája 2018, od: ThoughtCo.com
3. Tlačové knihy. 10.6 latice štruktúry v kryštalických tuhých látkach. Získané 26. mája 2018, od: OpenTextBC.Ac
4. Mdlák. (30. júna 2015). Typy kryštálových štruktúr. Získané 26. mája 2018, od: CrystalVisions-Film.com
5. HelMestine, Anne Marie, PH.D. (31. januára 2018). Druhy 
6. Kittel Charles (2013) Solid State Physics, Condensed Matter Physics (8. vydanie). Mravný.
7. Khi. (2007). Kryštalické štruktúry. Získané 26. mája 2018, od: Folk.Ntnu.Nie
8. Wikipedia. Bravais latices. Zdroj: In.Wikipedia.com.