Konvexná definícia polygónu, prvky, vlastnosti, príklady

A konvexný polygón Je to geometrická postava obsiahnutá v rovine, ktorá je charakterizovaná, pretože má všetky svoje uhlopriečky vo vnútri a jeho uhly merajú menej ako 180 °. Medzi jeho vlastnosti patria:

1) Pozostáva z n po sebe idúcich segmentov, kde sa posledný zo segmentov pripojí k prvému. 2) Žiadny zo segmentov nie je prekrížený takým spôsobom, že vymedzuje lietadlo vo vnútri a ďalšom vonkajšej strane. 3) Každý z uhlov vnútornej oblasti je striktne nižší ako plochý uhol.

postava 1. Polygóny 1, 2 a 6 sú konvexné. (Pripravil Ricardo Pérez).

Jednoduchý spôsob, ako určiť, či je polygón konvexný alebo nezohľadňuje čiaru, ktorá prechádza jednou zo svojich strán, čo určuje dve semiplány. Ak na každej línii, ktorá prechádza na jednej strane, sú druhé strany mnohouholníka v rovnakom semifreále, je to potom konvexný polygón.

[TOC]

Prvky mnohouholníka

Každý polygón pozostáva z nasledujúcich prvkov:

- Strany

- Vrcholy

Strany sú každý z po sebe idúcich segmentov, ktoré tvoria polygón. V mnohouholníku nemôže mať žiadny zo segmentov, ktoré ho tvoria.

Vrcholy sú bodmi Únie dvoch po sebe idúcich segmentov. V mnohouholníku sa počet vrcholov vždy rovná počtu strán.

Ak dve strany alebo segmenty polygónového kríža, máte krížový polygón. Bod prechodu sa nepovažuje za vrchol. Krížový polygón je nekonvexný polygón. Havarované polygóny sú krížené polygóny, a preto nie sú konvexné.

Môže vám slúžiť: analytická geometria

Ak má polygón všetky svoje strany rovnakej dĺžky, je tu pravidelný mnohouholník. Všetky bežné polygóny sú konvexné. 

Konvexné a nekonvexné polygóny

Obrázok 1 zobrazuje niekoľko polygónov, niektoré z nich sú konvexné a iné nie sú. Analyzme ich:

Číslo 1 je polygón s tromi zvratom (trojuholník) a všetky vnútorné uhly sú menšie ako 180 °, preto je to konvexný mnohouholník. Všetky trojuholníky sú konvexné polygóny.

Číslo 2 je štvorčlenný polygón (štvornásobný), kde žiadna zo strán nie je zachytená a tiež každý z vnútorných uhlov je menší ako 180 °. Je to potom štvorplňovaný konvexný polygón (konvexný kvadrilaterálny).

Na druhej strane, číslo 3 je štvorčlenný polygón, ale jeden z jeho vnútorných uhlov je väčší ako 180 °, takže nespĺňa podmienku konvexity. To znamená, že je to nekonvelovaný polygón.

Číslo 4 je štvorsegmentový (bočné) polygón, z ktorých dva sú zachytené. Štyri vnútorné uhly sú menšie ako 180 °, ale keď dve strany krížia, sú nekonvexným krížovým polygónom (krížové štvorkoliek).

Ďalším prípadom je číslo 5. Jedná sa o päťgón s päťdeskou, ale ako jeden z jeho vnútorných uhlov je väčší ako 180 °, potom existuje konkávny mnohouholník.

Nakoniec má číslo 6, ktoré má tiež päť strán, má všetky svoje vnútorné uhly menšie ako 180 °, takže ide o päťdesentový konvexný polygón (konvexný Pentagon).

Môže vám slúžiť: Chyba vzorkovania: vzorce a rovnice, výpočet, príklady

Konvexné vlastnosti polygónu

1- Nezkrytý mnohouholník alebo jednoduchý mnohouholník rozdeľuje rovinu, ktorá ju obsahuje do dvoch oblastí. Vnútorná oblasť a vonkajšia oblasť, čo je polygón hranica medzi týmito dvoma regiónmi.

Ale ak je polygón navyše konvexný, potom existuje vnútorná oblasť, ktorá je jednoducho príbuzná, čo znamená, že prijímanie akýchkoľvek dvoch bodov vnútorného regiónu, môže byť vždy zjednotený segmentom, ktorý patrí do celku vnútornej oblasti.

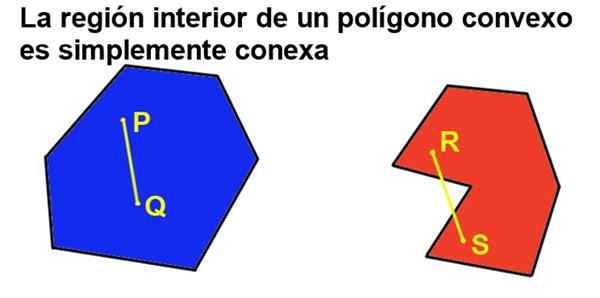Obrázok 2. Konvexný polygón jednoducho súvisí, zatiaľ čo konkávna nie je. (Pripravil Ricardo Pérez).

2- Celý vnútorný uhol konvexného polygónu je menší ako plochý uhol (180 °).

3- Všetky vnútorné body konvexného polygónu vždy patria k jednému zo čiastočne definovaných čiarom, ktorá prechádza dvoma po sebe idúcimi vrcholmi.

4- V konvexnom mnohouholníku sú všetky diagonály úplne obsiahnuté vo vnútornej oblasti mnohouholníka.

5- Vnútorné body konvexného polygónu patria do celku do konvexného uhlového sektora definovaného každým vnútorným uhlom.

6- Každý polygón, v ktorom sú všetky jeho vrcholy na obvode, je konvexný polygón, ktorý sa nazýva cyklický polygón.

7- Každý cyklický polygón je konvexný, ale nie každý konvexný polygón je cyklický.

8- Každý netrpený polygón (jednoduchý polygón), ktorý má všetky svoje strany rovnakej dĺžky, je konvexný a je známy ako pravidelný mnohouholník.

Diagonály a uhly v konvexných polygónoch

9- Celkový počet diagonálov konvexného polygónu N strany je daný nasledujúcim vzorcom:

Môže vám slúžiť: polybal grafika

N = ½ n (n - 3)

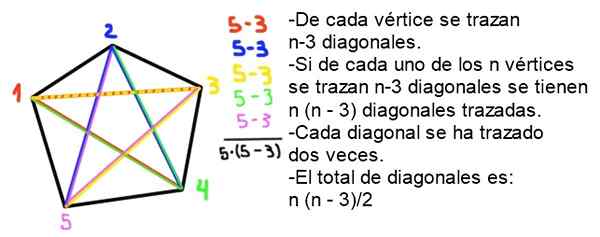
Demonštrácia: V konvexnom polygóne N strany každého vrcholu sú nakreslené n - 3 uhlopriečky, pretože samotný vrchol a dve susedné sú vylúčené. Pretože existujú N vrcholy, sú nakreslené celkom n - 2) diagonály, ale každý diagonál bol nakreslený dvakrát, takže počet diagonálov (bez opakovania) je N (N -2)/2.

10- Súčet vnútorných uhlov konvexného polygónu N Strany je daný nasledujúcim vzťahom:

S = (n - 2) 180 °

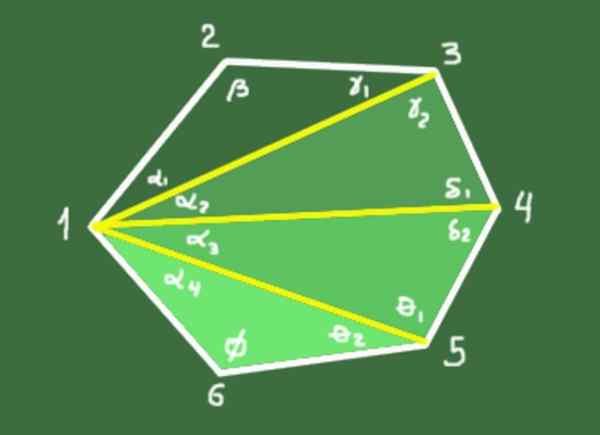
Demonštrácia: N-3 Diagonaly sú nakreslené zo vrcholu, ktorý definuje trojuholníky N-2. Súčet vnútorných uhlov každého trojuholníka je 180 °. Celkový súčet uhlov trojuholníkov N-2 je (n-2)*180 °, ktoré sa zhodujú so súčtom vnútorných uhlov mnohouholníka.

Príklady

Príklad 1

Cyklický šesťuholník, je to šesťprúdený polygón a šesť vrcholov, ale všetky vrcholy sú na rovnakom obvode. Všetok cyklický polygón je konvexný.

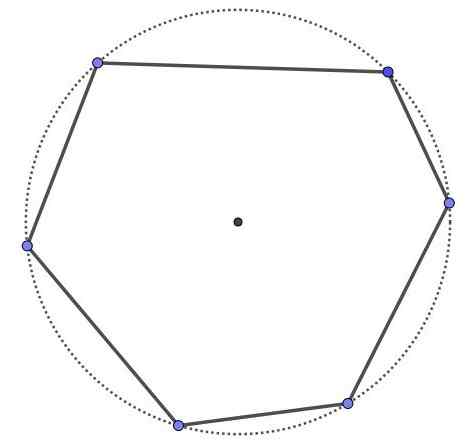Cyklický šesťuholník.

Príklad 2

Určiť hodnotu vnútorných uhlov pravidelného engonu.

RIEŠENIE: ENEGON je 9 -vedený polygón, ale tiež reguluje všetky jeho strany a uhly sú rovnaké.

Súčet všetkých vnútorných uhlov polygónu s 9 -odrazeným polygónom je:

S = (9 - 2) 180 ° = 7 * 180 ° = 1260 ° 

Existuje však 9 vnútorných uhlov rovnakej miery α, takže musí byť splnená nasledujúca rovnosť:

S = 9 a = 1260 °

Odkiaľ vyplýva, že a miera každého vnútorného uhla pravidelného engonu je:

a = 1260 °/9 = 140 °