Trigonometrické dôvody, príklady, cvičenia a aplikácie

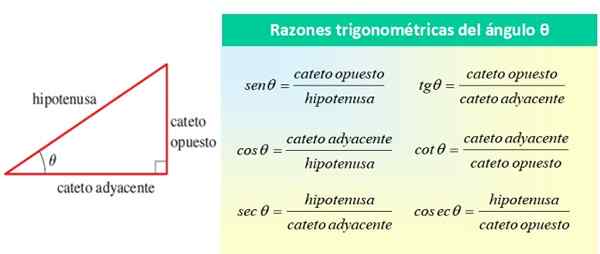
Ten trigonometrické dôvody Sú to kvocienty alebo dôvody, ktoré sa dajú urobiť s hodnotou bokov pravého trojuholníka. Tieto strany sú: dve kategórie, ktoré sa navzájom tvoria 90 °, a hypotenus, ktorá tvorí akútny uhol 9 s jednou z kategórií.

Je možné vytvoriť 6 kvocientov. Ich mená a príslušné skratky sú:

• Brease (sen)
• Coseno (cos)
• tangent (TG alebo Tan)
• COTANGENT (CTG alebo COTAN)
• Secante (sec) a
• Harvester (harmónia)

Všetky sa odvolávajú na uhol 9, ako je to znázornené na nasledujúcom obrázku:

postava 1. Trigonometrické dôvody akútneho uhla 9. Zdroj: f. Zapata.

Základné trigonometrické dôvody uhla 9 sú sin θ, cos θ a tan θ, zatiaľ čo zostávajúce dôvody možno vyjadriť z hľadiska týchto troch. Z predchádzajúceho obrázka vidíte to:

• Sec θ = 1/ cos θ
• poškodenie 9 = 1/ sin 9
• detská postieľka 9 = 1/tg 9

Veľkosť bokov trojuholníka neovplyvňuje hodnotu dôvodov, pretože dva trojuholníky, ktorých uhly merajú to isté, sú podobné trojuholníky a príslušné kvocienty medzi stranami majú rovnakú hodnotu.

[TOC]

Príklad

Napríklad vypočítame trigonometrické dôvody uhla 9 v nasledujúcich trojuholníkoch:

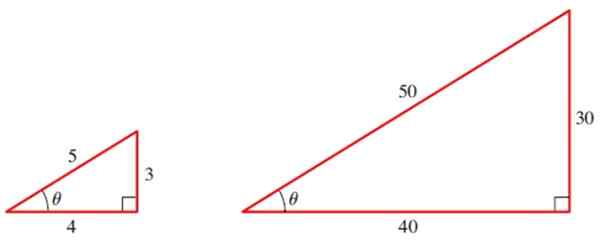Obrázok 2. Dva podobné trojuholníky majú rovnaké trigonometrické dôvody svojich uhlov. Zdroj: Stewart, J.Predbežné vycvičenie: matematika na výpočet.

Pre malý trojuholník máme tri základné dôvody uhla θ:

hriech θ = 3/5

cos θ = 4/5

TG 9 = ¾

A teraz vypočítame tri základné dôvody θ s veľkým trojuholníkom:

Sin θ = 30/50 = 3/5

cos θ = 40/50 = 4/5

TG θ = 30/40 = ¾

Dôležitý detail, ktorý je potrebné zvážiť, je nasledujúci: Sin θ aj cos θ sú menšie ako 1, pretože kategórie vždy merajú menej ako hypotenus. Naozaj:

sin θ = 3/5 = 0.6

cos θ = 4/5 = 0.8

Vyriešené cvičenia

V nasledujúcich cvičeniach sa vyžaduje vyriešiť pravý trojuholník, čo znamená nájsť dĺžku jeho troch strán a mieru jeho vnútorných uhlov, z ktorých jeden vždy meria 90 °.

Môže vám slúžiť: prvé -degree rovnice: vzorec, ako ich vyriešiť, napríklad cvičenia

Veta Pythagora sa vzťahuje na obdĺžnikové trojuholníky a je veľmi užitočná, keď sú známe dve strany a musí sa určiť chýbajúce. Veta hovorí:

Preprava² = oproti kateto² + susedný kateto²

Môžeme overiť vetu Pythagoras s malým trojuholníkom na obrázku 2, ktorého nohy sú 3 a 4. Na poradí, v ktorom sú kategórie prijaté. Aplikácia vety, ktorú máme:

Preprava² = 3² + 4² = 9 + 16 = 25

Preto je hypotenus:

Hypotenus = √25 = 5

- Cvičenie 1

Vypočítajte trigonometrické dôvody uhlov uvedených v týchto trojuholníkoch:

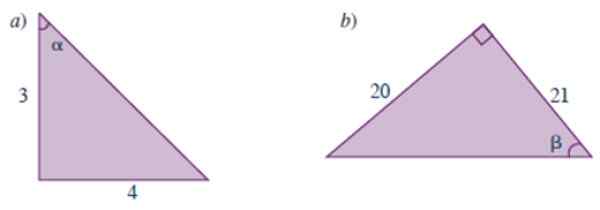Obrázok 3.- Trojuholníky za rok vyriešené 1. Zdroj: Carena, m. 2019. Príručka matematiky preduniverzity.

Roztok

Tento trojuholník je rovnaký na obrázku 3, ale žiadajú nás o trigonometrické dôvody druhého akútneho uhla, označené ako α. Vyhlásenie však neponúka hodnotu hypotenusu, avšak uplatňovaním vety Pythagory, o ktorej vieme, že to má hodnotu 5.

Dôvody sa dajú vypočítať priamo z definície, pričom pri výbere nohy, ktorá je opakom uhla α, je opatrná na výpočet Sen α. Pozrime sa:

• Sin α = 4/5
• cos α = 3/5
• TG a = 4/3
• COT α = ¾
• Sec a = 1/(3/5) = 5/3
• poškodenie a = 1/(4/5) = 5/4

A ako vidíme, hodnoty trigonometrických dôvodov sa vymenili. V skutočnosti sú a a 9 doplnkové uhly, čo znamená, že pridávajú 90 °. V tomto prípade je splnené, že sen α = cos θ a tak ďalej z iných dôvodov.

Riešenie B

Vypočítajme hypotenus trojuholníka cez vetu Pythagoras:

Preprava² = 20² + dvadsaťjeden² = 841

√841 = 29

Potom 6 trigonometrických dôvodov uhla β sú:

• Sen β = 20/29
• cos β = 21/29
• TG β = 20/21
• COT β = 21/20
• Sec β = 1/(21/29) = 29/21
• poškodenie β = 1/(20/29) = 20/29

Môže vám slúžiť: kombinované operácie

- Cvičenie 2

a) Nájdite hodnotu x na obrázku.

b) Vypočítajte obvod 3 zobrazených trojuholníkov.

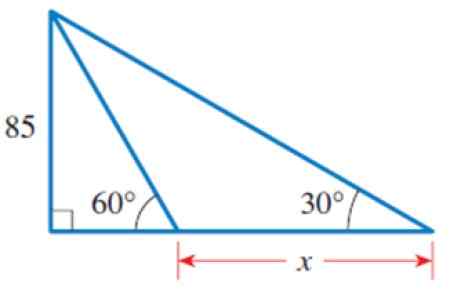Obrázok 4. Trojuholníky za rok vyriešené 2. Zdroj: Stewart, J. Predbežné vycvičenie: matematika na výpočet.

Roztok

Na obrázku môžeme identifikovať niekoľko trojuholníkov, najmä obdĺžnikový trojuholník vľavo, ktorý má kategóriu rovnú 85 a akútny uhol 60 °.

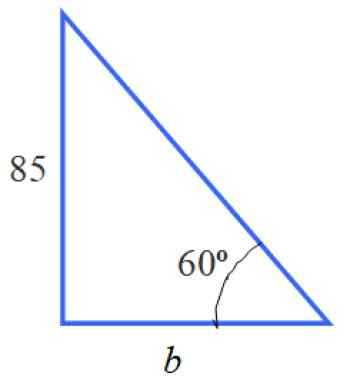Obrázok 5. Trojuholník vľavo.

S informáciami tohto trojuholníka môžeme vypočítať stranu b. Nie je to opatrenie, ktoré vyhlásenie žiada, ale poznať jeho hodnotu je predchádzajúci krok.

Na určenie vhodného dôvodu je TG 60 ° = 85 /b, pretože B je noha susedná so 60 ° a 85 je opakom uvedeným uhlom. Preto:

B = 85 / tg 60 ° = 85 / √3

Akonáhle je známy B, použijeme veľký a vonkajší obdĺžnikový trojuholník, ktorý má spoločnú stránku s predchádzajúcim trojuholníkom: ten, ktorý meria 85. Toto je kateto na rozdiel od uhla 30 °.

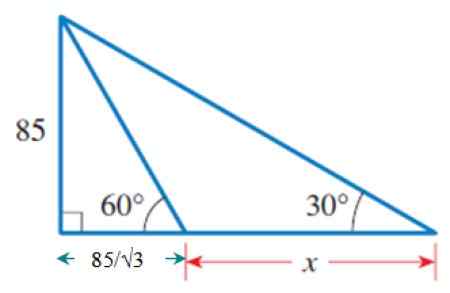Obrázok 6. Vonkajší trojuholník, ktorého časť základne je už známa.

Odtiaľ:

Kateto susediace s 30 ° = (85/√3) + x

Teraz môžeme zvýšiť nasledujúce:

85 / [(85 / √3) + x] = TG 30 °

Čo je v štvorcových zátvorkách vynásobte 30 ° TG:

85 = [(85/√3) + x]. TG 30 °

Uplatňovanie distribučnej vlastnosti násobenia:

85 = TG 30 °. (85/√3) + x. TG 30 °

Preto:

X.TG 30 ° = 85 - TG 30 °. (85/√3) = 85 [1 - TG 30 ° . (1/√3)] = 85 . (2/3) = 170/3

Výmena hodnoty TG 30 ° = √3 / 3:

x = (170/3) ÷ (√3 / 3) = 98.pätnásť

Riešenie B

Obvod malého trojuholníka

Byť h₁ Hypotenus tohto trojuholníka, ktorý možno vypočítať podľa Pythagorovej vety alebo z trigonometrického dôvodu, napríklad COS 60 °:

cos 60 ° = 85 / √3 / h₁→ H₁ = (85/√3) ÷ cos 60 ° = 98.1

Ak chcete nájsť P, obvod tohto trojuholníka, jednoducho pridáme 3 strany:

Môže vám slúžiť: Opisná štatistika: História, charakteristiky, príklady, koncepty

P = 85 + (85/√3) + 98.1 = 232.2

Obvod vonkajšieho trojuholníka

Byť h₂ na hypotenus vonkajšieho trojuholníka:

Sen 30 ° = 85 ÷ h₂  

h₂ = 85 ÷ hriech 30 ° = 170

Pre tento trojuholník je obvod:

P = 85 + [(85/√3) + 98.15] + 170 = 402.22

Obvod ne -rektanga trojuholníka

Z tohto trojuholníka už poznáme všetky jeho strany:

P = x + h₁ + h₂ = 98.15 + 98.15 + 170 = 366.3

Aplikácie trigonometrických dôvodov

Trigonometrické dôvody majú početné praktické aplikácie, napríklad výšky je možné vypočítať.

Predpokladajme, že vodná veža je 325 stôp od budovy. Pozorovateľ umiestnený v okne Všimnite si, že uhol výšky horného konca veže je 39 °, zatiaľ čo uhol depresie, s ktorou je viditeľná základňa veže, je 25 °. Zázraky:

a) Aká je výška veže?

b) Koľko je okno?

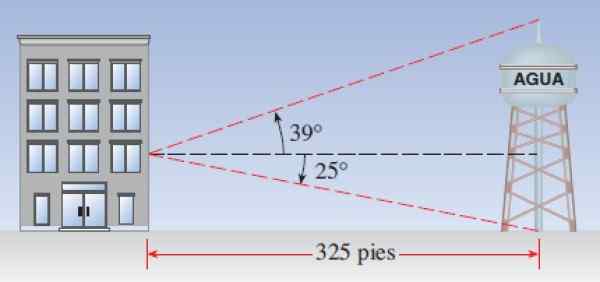Obrázok 7. Schéma na výpočet výšky Vista Torre z budovy. Zdroj: Stewart, J. Predbežné vycvičenie: matematika na výpočet.

Roztok

Od kateto oproti 39 horného trojuholníka dostaneme časť odpovede:

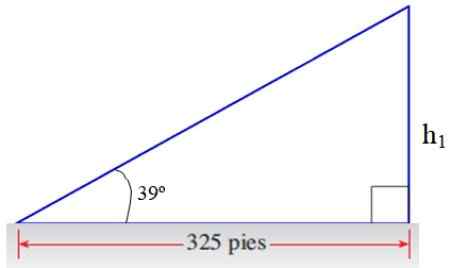Obrázok 8. Trojuholník na cvičenie aplikácie. Zdroj: f. Zapata.

h₁/325 = TG 39 ° → H₁ = 325 . Tg 39 ° stôp = 263.2 stopy

Podobným spôsobom dostávame zvyšok výšky veže, nazývaný H₂ Z dolného trojuholníka:

h₂/325 = TG 25 ° → H₂ = 325 . Tg 25 ° stôp = 151.6 stôp

Celková výška veže je h₁ + h₂ = 263.2 + 151.6 stôp = 414.7 stôp.

Riešenie B

Okno je presne vo výške h₂ pôda

h₂ = 151.6 stôp.

Odkazy

1. Carena, m. 2019. Príručka matematiky preduniverzity. Národná univerzita pobrežia.
2. Hoffman, J. Výber matematických problémov. Zväzok 3.
3. Jiménez, r. 2008. Algebra. Sála.
4. Stewart, J. 2006. Predbežné vycvičenie: matematika na výpočet. 5. Vydanie. Učenie sa.
5. Zill, D. 1984. Algebra a trigonometria. McGraw Hill.