Aký je vzťah medzi rhombom a obdĺžnicou oblasťou?

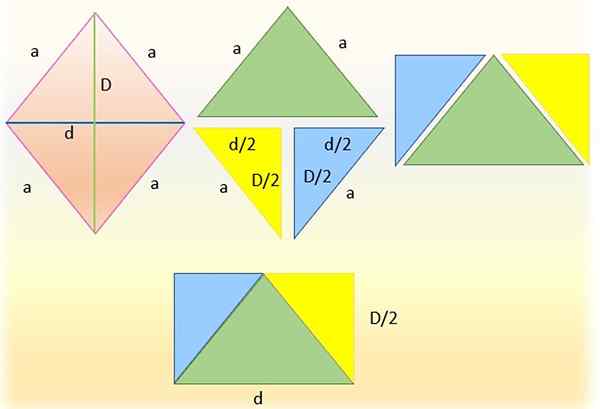
Rozklad rhombu na získanie obdĺžnika. Zdroj: f. Zapata

Je možné vypočítať oblasť kostra (a niektoré ďalšie geometrické čísla) z oblasti trojuholníka alebo príbuzného kvadriterálu, ako je rovnobežník alebo obdĺžnik.

Obdĺžnik a plocha rovnobežníka sú rovnaké: sa vypočíta ako produkt medzi základňou obrázku a jeho výškou vzhľadom na túto základňu. Oblasť trojuholníka je polopriepustný produkt medzi jeho základňou a výškou.

Tieto vzorce sa dajú ľahko zapamätať, aj keď geometria samozrejme ponúka exkluzívny vzorec pre oblasť Rhombus, ktorý pozná mieru jej hlavných a menších diagonálov označených ako D a D:

Je možné odvodiť tento výraz prostredníctvom sekvencie znázornenej na obrázku vyššie.

Za týmto účelom je kosoštvorca vľavo rozrezaný jedným z jej diagonálov, ktorý bol vyrobený v odseku obrázkov menším diagonálom, čím sa získa dva trojuholníky. Horný trojuholník (v zelenej) je vľavo a dolný je rozdelený zase na dva trojuholníky, rezané na polovicu hlavného diagonálneho, čím získate rovnaké modré a žlté obdĺžniky.

Potom sa hypoteny týchto trojuholníkov zhodujú so stranami zeleného trojuholníka, pretože merajú to isté, to je „a“. A konečne sa získa obdĺžnik, ktorého základňa je dolná „D“ diagonálna a ktorej výška je polovica hlavného diagonálneho, to znamená: „D/2“.

Takto vytvorená oblasť obdĺžnika sa zhoduje presne o oblasť kosoštvorca, preto je možné potvrdiť, že:

Môže vám slúžiť: trinomial

Do _diamant = (základňa × výška) _obdĺžnik = D × (d/2)

Výsledkom, že, ako je vidieť.

Rombo a plocha rovnobežníka

Oblasť Rhombus je tiež v spojení s rovnoprávnou časťou rovnobežníka, pretože obe geometrické postavy sú ploché a patria do rodiny štvoruholníkov. Napríklad na nasledujúcom obrázku je vľavo rhombus a rovnobežník vpravo.

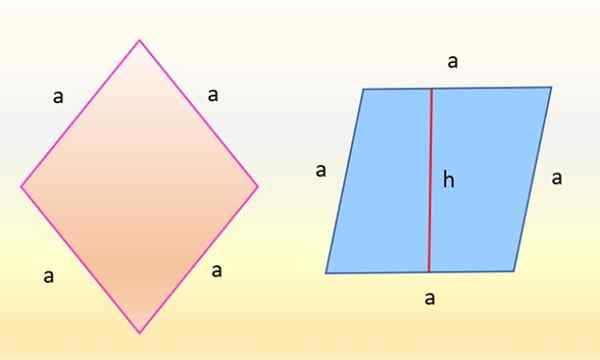Oblasť Rhombus vľavo je rovnaká ako vpravo na rovnobežníku vpravo. Zdroj: f. Zapata

Ukazuje sa, že obrázky sú identické, pretože to, čo sa zmenilo, je iba orientácia. Rhobus vľavo, v ružovej farbe, ktorého strany majú rovnaké opatrenie: a, je otočená takým spôsobom, že jedna z jeho strán je úplne vodorovná. Potom rhombus má tvar modrého rovnobežníka vpravo.

A plocha tohto rovnobežníka je tiež produktom medzi základňou „A“ a výškou vzhľadom na túto základňu nazývanú „H“ na obrázku, preto:

Do _{rovnobežník} = A × H

Pretože je to rovnaká hodnota, oblasť je identická a podľa toho, že:

Do _diamant = A × H

Poznanie a h rovnobežníka sa tak vypočítava jeho oblasť a bude sa zhodovať s oblasťami kostra Rhombus.

Oblasť Rombo napísaná v obdĺžniku

Ďalší vzťah medzi Rhombusom a obdĺžnikom sa objaví, keď je prvý zaregistrovaný vo vnútri druhého. Ak k tomu dôjde, vrcholy kosoštvorca sa zhodujú so stredom bokov obdĺžnika, ktorý je zobrazený nižšie:

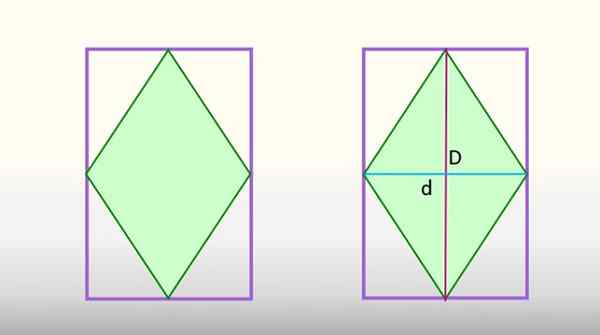Oblasť Rhombus vpísaná do obdĺžnika je rovnocenná s polovicou obdĺžnikovej oblasti. Zdroj: f. Zapata

Toto ustanovenie robí hlavné a menšie uhlopriečky kosoštvorca, postava je rozdelená na 8 rovnakých trojuholníkov, z ktorých 4 zodpovedajú kostolu v zelenej farbe a ďalšie 4 sú súčasťou obdĺžnika. Keby sa tieto posledné 4 trojuholníky spojili, vytvorili by polovicu obdĺžnika a 4 trojuholníky Rhombus, druhé.

Môže vám slúžiť: Isosceles trojuholník

Preto oblasť Rhombus je rovnocenná s polovicou oblasti obdĺžnika, v ktorej je registrovaná, čo uvádza, že:

Do_diamant = A_obdĺžnik / 2

Toto sa ľahko overuje výpočtom plochy jedného z trojuholníkov a vynásobením 4, pretože sú rovnaké. Oblasť akéhokoľvek trojuholníka je polovica produktu medzi základňou a jeho výškou:

Do _trojuholník = báza × výška /2

Z predchádzajúceho obrázku sa pozoruje, že základňa jedného z trojuholníkov je d/2 a výška je d/2, ktorá nahradenie v predchádzajúcom vzorec dáva:

Do _trojuholník = (d /2) × (d /2) /2 = (d × d) /8

Vynásobenie tohto výsledku 4, aby ste mali oblasť Rhombus:

Do _diamant = 4 (d × d) /8 = (d × d) /2

Polovica obdĺžnika je:

Do _obdĺžnik / 2 = báza × výška / 2

Pretože spodná časť obdĺžnika je D a jeho výška je D, zostáva:

Do_obdĺžnik / 2 = d × d/ 2

Čo je presne oblasť registrovaného kostra. Predpokladá sa, že:

Oblasť kostra zaregistrovaného v obdĺžniku je rovnocenná s polovicou tejto oblasti tohto.

Vyriešené cvičenia

Cvičenie 1

Koľko je oblasť Rhombus, ktorej hlavné diagonálne opatrenia 14.6 cm a dolný diagonálny 9.8 cm?

Riešenie

Výmenou D = 14.6 cm a d = 9.8 cm v receptúre v oblasti Rhombus:

Hľadaná oblasť je:

Do _diamant = 14.6 cm × 9.8 cm = 143.1 cm²

Cvičenie 2

Na obrázku predchádzajúcej časti je hlavná diagonála kosoštvorca zaregistrovaná v obdĺžnikových opatreniach d = 30 cm a oblasť obdĺžnika má hodnotu 210 cm². Žiada sa na výpočet:

a) dĺžka menšej uhlopriečky

Môže vám slúžiť: linka a segment semiférií

b) oblasť kosoštvorca dvoma spôsobmi: prvý cez oblasť obdĺžnika a druhý s použitím vzorca oblasti rhombu. Skontrolujte, či je výsledok rovnaký.

Roztok

Obdĺžnik je produkt medzi jeho základňou a jeho výškou. Najväčšou diagonálom je jeho výška, zatiaľ čo najmenšia diagonálna D by bola základňa. Pomocou vzorca oblasti a výmenou hodnôt príkazu máte:

Do _obdĺžnik = báza × výška = d × 30 cm = 210 cm²

Potom stojí základňa:

D = 210 cm² / 30 cm = 7 cm

Riešenie B

Ako je uvedené vyššie, oblasť Rhombus je polovica oblasti obdĺžnika, a to je známe:

Do _diamant = 210 cm² /2 = 105 cm²

Výsledok sa skontroluje okamžite a nahradí sa vo vzorci:

Diagonaly sú už známe: d = 30 cm, d = 7 cm, potom:

Do _diamant = 30 cm × 7 cm /2 = 105 cm²

Je dokázané, že, ako sa očakávalo, oblasť Rhombus je v oboch prípadoch rovnaká.