Coplanares bodový rovnica, príklad a vyriešené cvičenia

Ten Body Coplanares Všetci patria do toho istého lietadla. Dva body sú vždy koplanány, pretože tieto body definujú čiaru, cez ktorú prechádzajú ploché infinity. Potom obidva body patria do každého z plánov, ktoré prechádzajú líniou, a preto budú vždy koplanány.

Na druhej strane, tri body definujú jednu rovinu, z ktorých je nasledované, že tri body budú vždy koplanány do lietadla, ktoré určujú.

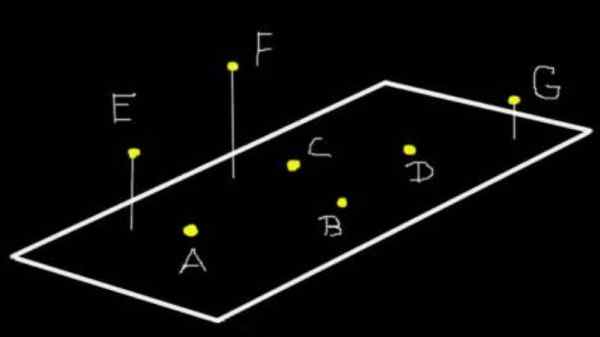
postava 1. A, B, C a D sú koplanány do roviny (Ω). E, F a G nie sú koplanány A (Ω), ale ak sú koplanány do lietadla, ktoré traja definujú. Zdroj: f. Zapata.

Viac ako tri body môžu byť koplanárne alebo nie. Napríklad na obrázku 1, body A, B, C a D sú koplanáry do roviny (co). Ale E, F a G nie sú koplanány A (Ω), hoci sú to koplanány do lietadla, ktoré traja definujú.

[TOC]

Rovnica lietadla Daná tromi bodmi

Rovnica roviny určená tromi známymi bodmi A, B, C je matematický vzťah, ktorý zaručuje, že akýkoľvek bod P generických súradníc (x, y, z), ktorý spĺňa rovnicu, patrí do uvedenej roviny. 

Predchádzajúce vyhlásenie je rovnocenné s tvrdením, že ak P koordinácie (x, y, z) spĺňa rovnicu roviny, potom bude uvedený bod na copatar s tromi bodmi a, b, c, ktoré určujú rovinu.

Ak chcete nájsť rovnicu uvedenej roviny, začnime nájdením vektorov AB a Ac:

AB = [Bx - seker, od - ay, bz - az]

Ac = [Cx - ax, cy - ay, cz - az]

Vektorový produkt AB X Ac Výsledkom je kolmý alebo normálny vektor do roviny určeného bodmi a, b, c.

Akýkoľvek bod súradníc (x, y, z) patrí do roviny, ak je pravda, že vektor AP je kolmo na vektor AB X Ac, čo je zaručené, ak je splnené:

Môže vám slúžiť: decagon: pravidelné, nepravidelné, vlastnosti, príklady

AP • (AB X Ac) = 0

To je rovnocenné s tvrdením, že trojitý produkt AP, AB a Ac Byť nula. Predchádzajúcu rovnicu je možné napísať matricovým spôsobom:

Príklad

Nech body A (0, 1, 2); B (1, 2, 3); C (7, 2, 1) a D (do, 0, 1). Aká hodnota by mala mať do takže štyri body sú koplanány?

Riešenie

Na nájdenie hodnoty A je potrebné, aby bod D bol súčasťou roviny určeného pomocou A, B a C, čo je zaručené, ak sa rovnica roviny stretne.

Rozvoj determinantu, ktorý máme:

A (-1-1) + 1 (-1 -7) -1 (1 -7) = -2a -8 + 6 = -2a -2 = 0

Predchádzajúca rovnica to naznačuje A = -1 Splniť rovnosť. Inými slovami, jediný spôsob, ako tento bod D (do, 0.1) byť koplanárny s bodmi A, B a C je taký do Valga -1. Inak to nebude koplanár.

Vyriešené cvičenia

- Cvičenie 1

Lietadlo pretína karteziánske osi x, y, z v 1, 2 a 3. Križovatka uvedenej roviny so osami určuje body A, B a C. Nájdite zložku DZ bodu D, ktorej karteziánske komponenty sú:

 D (-dz, dz+1, dz) 

Pod podmienkou, že D je koplanárna s bodmi A, B a C. 

Riešenie

Ak je známe odpočúvanie roviny s karteziánskymi osami, je možné použiť segmentálnu formu rovnice rovnice:

x/1 + y/2 + z/3 = 1

Keďže bod D musí patriť do predchádzajúcej roviny, musíte:

-DZ/1 + (DZ + 1)/2 + DZ/3 = 1

To znamená:

-DZ + DZ/2 + ½ + DZ/3 = 1

DZ (-1 + ½ + ⅓) = ½ 

DZ (-1/6⅙) = ½ 

DZ = -3 

Z vyššie uvedeného sleduje, že bod D (3, -2, -3) je spojený s bodmi A (1, 0, 0); B (0, 2, 0) a C (0, 0, 3).

Môže vám slúžiť: trojuholníkové kritériá podobnosti

- Cvičenie 2

Určiť, či body A (0, 5, 3); B (0, 6, 4); C (2, 4, 2) a D (2, 3, 1) sú koplanáry.

Riešenie

Vytvárame maticu, ktorej rady sú súradnice D-A, B-A a C-A. Potom sa vypočíta determinant a overuje sa, či nula.

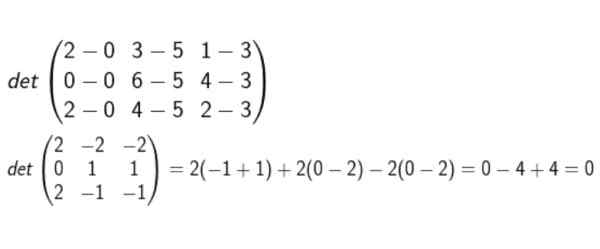
Po vykonaní všetkých výpočtov sa dospelo k záveru, že sú to koplanány.

- Cvičenie 3

Vo vesmíre sú uvedené dve riadky. Jedným z nich je riadok (R), ktorej parametrická rovnica je:

(R): x = 1 + 2 λ; y = 1 - λ; Z = 1

A druhým je čiara (riadky), ktorej rovnica je:

(S): x + 2 y = 1; Z = -1

Demonštrovať, že (r) a (S) sú priame coplanarium, to znamená, že sú v rovnakom lietadle.

Riešenie

Začnime svojvoľne dva body na linke (R) a dva na riadku (-y):

Rovno (r): λ = 0; A (1, 1, 1) a λ = 1; B (3, 0, 1)

Poď robiť x = 0 na riadku=> y = ½; C (0, ½, -1). A na druhej strane, ak áno y = 0 => x = 1; D (1, 0, -1).

To znamená, že sme vzali body A a B, ktoré patria do riadku (R) a bodov C a D, ktoré patria do riadku (-y). Ak sú tieto body coplanáres, potom budú tiež dve riadky.

Teraz sa rozhodneme ukázať ako otočenie a potom nájdeme súradnice vektorov AB, Ac a Reklama. Týmto spôsobom dostanete:

B - A: (3-1, 0 -1, 1 - 1) => AB= (2, -1, 0)

C -a: (0-1, 1/2 -1, -1 -1) => Ac= (-1, -1/2, -2)

D -a: (1-1, 0 -1, -1 -1) => Reklama= (0, -1, -2)

Ďalším krokom je zostavenie a výpočet determinant, ktorého prvým riadkom sú vektorové koeficienty AB, Druhý riadok je Ac a tretí riadok vektor Reklama:

Môže vám slúžiť: Miletus takúto vetu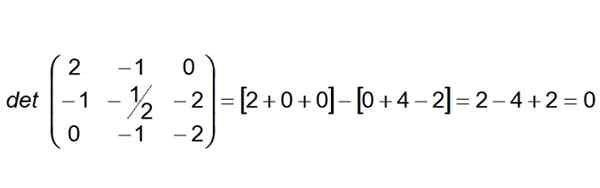

Keď sa determinant ukáže ako nulová, potom môžeme dospieť k záveru, že štyri body sú coplanarios. Okrem toho sa dá povedať, že riadky (R) a (S) sú tiež koplanány.

- Cvičenie 4

Čiary (R) a (S) sú koplanány, ako je uvedené v cvičení 3. Nájdite rovnicu lietadla, ktorá ich obsahuje.

Riešenie

Body A, B, C úplne definujú túto rovinu, ale chceme uložiť, že akýkoľvek bod X súradníc (x, y, z) patrí k tomu istému.

X - a: (x -1, y -1, z - 1) => Sekera= (X -1, y -1, z -1)

B - A: (3-1, 0 -1, 1 - 1) => AB= (2, -1, 0)

C -a: (0-1, 1/2 -1, -1 -1) => Ac= (-1, -1/2, -2)

Takže X patrí do roviny definovanej A, B, C a v ktorej sú obsiahnuté čiary (R) a (S), je potrebné, aby determinant vytvorený v prvom riadku zrušil zložky z komponentov Sekera, v druhej AB A v treťom od tých Ac:

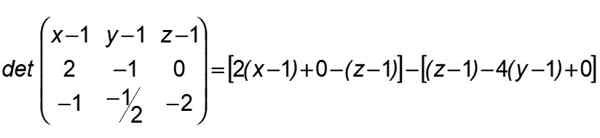
Po tomto výsledku sa zoskupujeme týmto spôsobom:

2 (x-1) + 4 (y-1) -2 (z-1) = 0

A okamžite je zrejmé, že ho možno prepísať takto:

x - 1 + 2y - 2 - z + 1 = 0

Preto x + 2y - z = 2 je rovnica roviny, ktorá obsahuje čiary (r) a (S).

Odkazy

1. Fleming, w. 1989. Matematika. Prentice Hall PTR.
2. Kolman, B. 2006. Lineárna algebra. Pearson Vzdelanie.
3. Lojálny, j. M. 2005. Plochá analytická geometria. Mérida - Venezuela: Venezuelský redaktor C. Do.
4. Navarro, Rocio. Vektory. Získané z: Knihy.Riadenie.co.ísť.
5. Pérez, C. D. 2006. Predbežné vyfarbenie. Pearson Vzdelanie.
6. Prenowitz, w. 2012. Základné koncepty geometrie. Rowman a Littlefield.
7. Sullivan, m. 1997. Predbežné vyfarbenie. Pearson Vzdelanie.