Vnútorné a vonkajšie konjugované uhly príklady, cvičenia

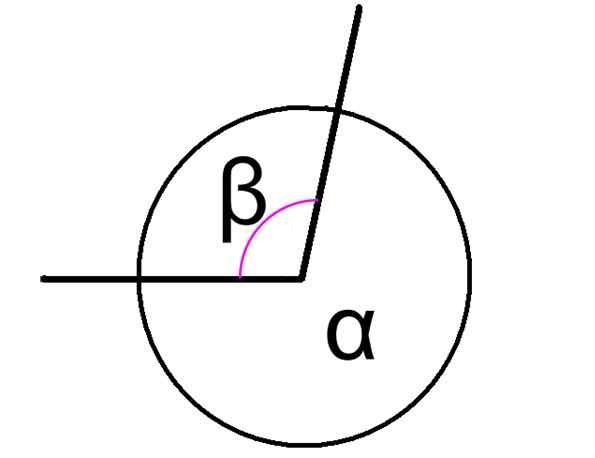
Ten konjugované uhly Sú to tie, ktoré sa pridávajú v dôsledku 360 °, bez ohľadu na to, či tieto uhly susedia alebo nie. Obrázok 1 zobrazuje dva konjugované uhly označené ako a a p.

V takom prípade majú uhly a a p postavy spoločný vrchol a ich strany sú bežné, preto sú susedné. Vzťah medzi nimi je vyjadrený takto:

a + β = 360 °

postava 1. Dva konjugované centrálne uhly, suma. Zdroj: Wikimedia Commons. Nie je k dispozícii žiadny strojovo čitateľný autor. Thiago R Ramos predpokladal (na základe nárokov na autorské práva). [CC BY-SA 3.0 (http: // creativeCommons.Org/licencie/By-SA/3.0/)] Je to klasifikácia uhlov svojou sumou. Ďalšie dôležité definície zahŕňajú komplementárne uhly, ktorého súčet je 90 ° a doplnkové uhly, čo predstavuje 180 °.

Na druhej strane, zvážme teraz dve paralelné čiary rezané secantom, ktorého dispozícia je uvedená vtedy:

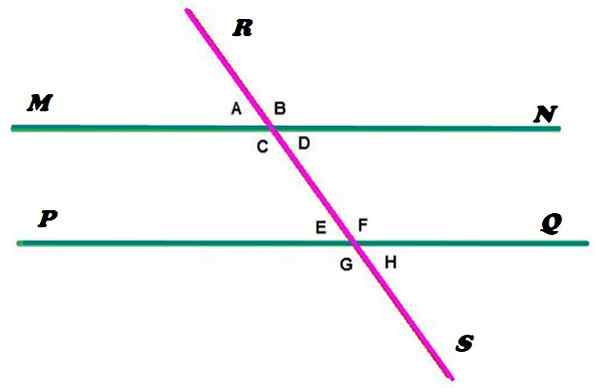
Obrázok 2. Paralelné čiary rezané sekundom. Zdroj: f. Zapata.

Čiary Mn a PQ sú rovnobežné, zatiaľ čo čiara RS suší, pretína paralely v dvoch bodoch. Ako je vidieť, táto konfigurácia určuje tvorbu 8 uhlov, ku ktorým bola označená malými písmenami.

Podľa definície uvedenej na začiatku sú uhly A, B, C a D konjugované. A rovnako sú E, F, G a H, pretože obidva prípady sa splnia:

A+B+C+D = 360 °

A

E+f+g+h = 360 °

Pre túto konfiguráciu sa konjugujú dva uhly, ak sú na rovnakej strane vzhľadom na sušenie RS a oba sú interné alebo externé. V prvom prípade sa hovorí o uhloch Vnútorné konjugáty, Zatiaľ čo v druhej, sú uhly vonkajší konjugát.

[TOC]

Príklady

Na obrázku 2 sú vonkajšie uhly tie, ktoré sú mimo regiónu vymedzené líniami Mn a PQ, sú to uhly A, B, G a H. Zatiaľ čo uhly, ktoré sú medzi týmito dvoma čiarami, sú C, D, E a F.

Môže vám slúžiť: Coplanares body: rovnica, príklad a vyriešené cvičenia

Teraz je potrebné analyzovať, ktoré uhly sú vľavo a ktoré napravo od secantu.

Vľavo od RS sú uhly a, c, e a g. A napravo sú B, D, F a H.

Okamžite pokračujeme v určení párov konjugovaných uhlov podľa definície uvedenej v predchádzajúcej časti:

-A a G, vonkajšie a naľavo od RS.

-D a F, vnútorné a napravo od Rs.

-B a H, vonkajšie a napravo od Rs.

-C a E, vnútorné a naľavo od RS.

Vlastnosť konjugovaných uhlov medzi paralelnými čiarami

Konjugované uhly medzi rovnobežnými čiarami sú doplnkové, to znamená, že ich súčet sa rovná 180 °. Týmto spôsobom je na obrázku 2 splnené nasledujúce:

A + G = 180 °

D + F = 180 °

B + H = 180 °

C + E = 180 °

Zodpovedajúce uhly páry pre paralelné čiary

Sú to tie, ktoré sú na rovnakej strane sušiacej línie, nie sú susedné a jeden z nich je vnútorný a druhý je vonkajší. Je dôležité si ich vizualizovať, pretože ich miera je rovnaká, pretože sú opačnými uhlami podľa vrcholu.

Pri návrate na obrázok 2 sú zodpovedajúce uhly identifikované ako:

-A e

-C a g

-B a F

-D a h

Vnútorné uhly kvadrilaterálneho

Kvadrilaterály sú 4 -potlačené polygóny, vrátane štvorca, obdĺžnika, lichobežníka, rovnobežníka a kosoštvorca, napríklad napríklad. Bez ohľadu na svoju formu, v ktorejkoľvek z nich je splnené, že súčet jeho vnútorných uhlov je 360 ​​°, preto dodržiavajú definíciu uvedenú na začiatku.

Pozrime sa na niektoré príklady kvadrilaterálov a ako vypočítať hodnotu jeho vnútorných uhlov podľa informácií o predchádzajúcich sekciách:

Môže vám slúžiť: Aké sú 7 prvkov obvodu?

Príklady

a) Tri uhly kvadriterálneho opatrenia 75 °, 110 ° a 70 °. Koľko by mal zostávajúci uhlový meranie?

b) Nájdite hodnotu uhla ∠Q na obrázku 3 i.

c) Vypočítajte, koľko meria uhol ∠A na obrázku 3 II.

Roztok

Nech α je chýbajúci uhol, splní sa, že:

a + 75 ° + 110 ° + 70 ° = 360 → α = 105 °

Riešenie B

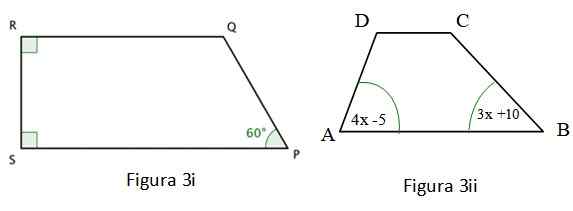
Obrázok 3i je Lichobežník A dva z jeho vnútorných uhlov sú rovné, ktoré boli poukázané na farebné štvorec v rohoch. Pre tento štvornásobný je overený nasledujúci:

∠R + ∠S + ∠P + ∠Q = 360 °; ∠S = ∠R = 90 °; ∠P = 60 °

Preto:

∠ q = 2 x 90 ° + 60 ° = 240 °

Riešenie c

Kvadrilaterál na obrázku 3 II je tiež lichobežník, pre ktorý sa splní nasledujúce:

∠A + ∠B + ∠C + ∠D = 360 °

Preto:

4x -5 + 3x + 10 +180 = 360

7x + 5 = 180

X = (180 - 5) / 7

x = 25

Na určenie uhol požadovaného vo vyhlásení sa používa, že ∠A = 4x - 5. Výmena hodnoty X predtým vypočítaná, že ∠A = (4 × 25) -5 = 95 °

Cvičenia

- Cvičenie 1

S vedomím, že jeden z zobrazených uhlov má hodnotu 125, nájdenie opatrení zvyšných 7 uhlov na nasledujúcom obrázku a odôvodnenie odpovedí.

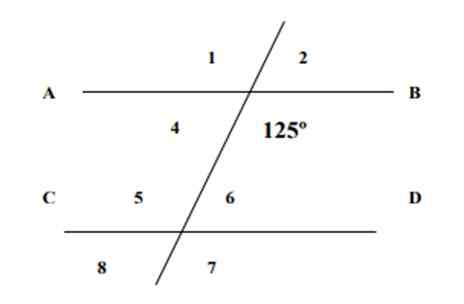Obrázok 4. Čiary a uhly cvičenia 1. Zdroj: f. Zapata.

Riešenie

Uhol 6 a uhol 125 sú vnútorné konjugáty, ktorých suma má hodnotu 180 °, podľa vlastníctva konjugovaných uhlov:

∠6 + 125 ° = 180 ° → ∠6 = 180 ° - 125 ° = 55 °

Na druhej strane ∠6 a ∠8 sú opačné uhly podľa vrcholu, ktorého opatrenie je rovnaké. Preto ∠8 meria 55 °.

Môže vám slúžiť: Vektorová algebra

Uhol ∠1 je tiež proti vrcholu pri 125, potom môžeme potvrdiť, že ∠1 = 125 °. Môžeme tiež osloviť skutočnosť, že zodpovedajúce páry uhlov majú rovnaké opatrenie. Na obrázku sú tieto uhly:

∠7 = 125 °

∠2 = ∠6 = 55 °

∠1 = ∠5 = 125 °

∠4 = ∠8 = 55 °

- Cvičenie 2

Nájdite hodnotu X na nasledujúcom obrázku a hodnoty všetkých uhlov:

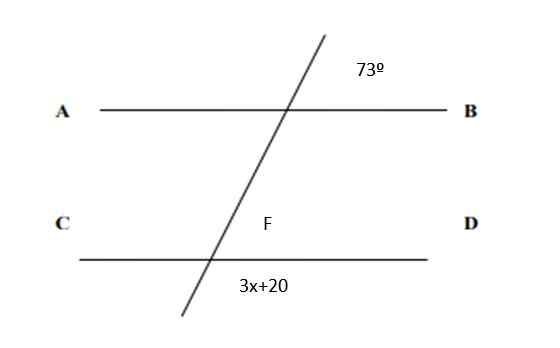Obrázok 5. Riadky a uhly pre cvičenie 2. Zdroj: f. Zapata.

Riešenie

Pretože sú to zodpovedajúce páry, z toho vyplýva, že f = 73 °. A na druhej strane, súčet konjugovaných párov je preto 180 °:

3x + 20 ° + 73 ° = 180 °

3x = 180 ° - 73 ° -20 ° = 87

Nakoniec hodnota X je:

x = 87/3 = 29

Pokiaľ ide o všetky uhly, objavia sa uvedené na nasledujúcom obrázku:

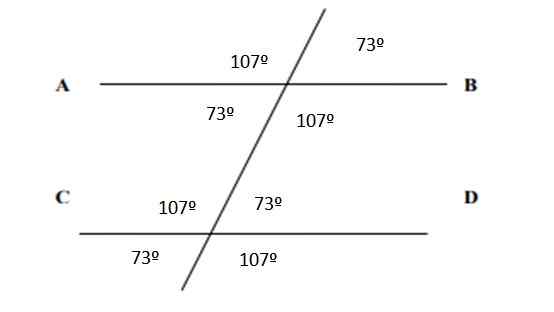Obrázok 6. Uhly, ktoré vedú k cvičeniu 2. Zdroj: f. Zapata.

Odkazy

1. Uhlové skupiny. Doplnkové, doplnkové a vysvetľujúce uhly. Získané z: Thisiget.com/ com/
2. Baldor, a. 1983. Geometria plochej a priestoru a trigonometrie. Kultúrna vlastná skupina.
3. Corral, m. Matematické librettexts: uhly. Získané z: matematiky.Librettexts.orgán.
4. Matematika. Klasifikácia a konštrukcia uhlov ich meraním. Získané z: Matmenia.com/ com/
5. Wentworth, G. Geometria planéty. Získané z: Gutenberg.orgán.
6. Wikipedia. Konjugované uhly. Obnovené z: je.Wikipedia.orgán.