Vysvetlenie zloženej proporcionality, tri zložené pravidlo, cvičenia

Ten Kompozitná alebo viacnásobná proporcionalita Je to vzťah medzi viac ako dvoma veľkosťami, kde je možné pozorovať priamu a inverznú proporcionalitu medzi údajmi a neznámymi. Je to pokročilejšia verzia jednoduchej proporcionality, hoci techniky použité v oboch postupoch sú podobné.

Napríklad, ak je potrebných 7 ľudí na stiahnutie 10 ton tovaru za 3 hodiny, zložená proporcionalita sa dá použiť na výpočet, koľko ľudí bude potrebných na stiahnutie 15 ton za 4 hodiny.

Zdroj: Pixabay.com

Na zodpovedanie tejto otázky je vhodné urobiť tabuľku hodnôt na štúdium a súvislosť s veľkosťou a neznámymi.

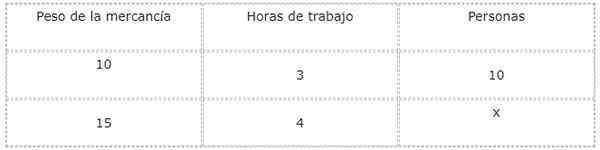
Analyzujú sa typy vzťahov medzi každou veľkosťou a súčasným neznámym, čo v tomto prípade zodpovedá počtu ľudí, ktorí budú pracovať.

Keď sa zvyšuje váha tovaru, zvyšuje sa aj počet ľudí potrebných na stiahnutie. Z tohto dôvodu je vzťah medzi hmotnosťou a pracovníkmi priamy.

Na druhej strane zvýšením počtu pracovníkov sa pracovné hodiny znižujú. Z tohto dôvodu je vzťah medzi ľuďmi a pracovným časom inverzný.

[TOC]

Ako vypočítať proporcionality zlúčeniny

Na vyriešenie príkladov, ako je predchádzajúci, sa väčšinou používa metóda troch zložených pravidiel. To spočíva v nadviazaní typov vzťahov medzi veľkosťami a neznámymi a potom predstavovaním produktu medzi frakciami.

Pokiaľ ide o počiatočný príklad, frakcie zodpovedajúce tabuľke hodnôt sú usporiadané takto:

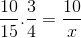
Ale pred vyriešením a vyčistením neznáma sa musia zlomky zodpovedajúce inverznému vzťahu zvrátiť. Že v tomto prípade zodpovedá časovej premennej. Týmto spôsobom bude operácia vyriešená:

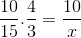
Ktorého jediným rozdielom je investícia frakcie zodpovedajúcej premenlivému času 4/3. Hodnota X je prevádzkovaná a jasná.

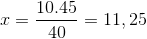
Preto je potrebných viac ako jedenásť ľudí na stiahnutie 15 ton tovaru za 4 hodiny alebo menej.

Vysvetlenie

Proporcionalita je konštantný vzťah medzi veľkosťou. Existujú priamo a nepriamo proporcionálne vzťahy, čím definujú parametre jednoduchej alebo zloženej proporcionality.

Nasmerovať tri pravidlo

Skladá sa z pomeru pomeru medzi premennými, ktoré pri modifikácii vykazujú rovnaké správanie. Je veľmi častá pri výpočte percentuálnych podielov týkajúcich sa rôznych veľkostí sto, kde sa oceňuje jeho základná štruktúra.

Ako príklad môžete vypočítať 15% zo 63. Na prvý pohľad, uvedené percento nie je možné vidieť jednoduchým spôsobom. Ale implementácia pravidla troch môžete vytvoriť nasledujúci vzťah: ak je 100% 63, potom 15%, koľko to bude?

Môže vám slúžiť: Faktorová veta: Vysvetlenie, príklady, cvičenia

100%-63

15%-x

A zodpovedajúca operácia je:

(pätnásť% . 63) / 100% = 9,45

Kde sú percentuálne znaky zjednodušené a dosiahne sa hodnota 9,45, ktorý predstavuje 15% zo 63.

Tri inverzné pravidlo

Ako už názov napovedá, v tomto prípade je vzťah medzi premennými naopak. Pred pokračovaním v výpočte musí byť nadviazaný inverzný vzťah. Jeho postup je homológny s tromi priamymi pravidlami, s výnimkou investícií do frakcie, ktorá sa má vypočítať.

Napríklad 3 maliari potrebujú na dokončenie steny 5 hodín. Koľko hodín by skončili 4 maliari?

V tomto prípade je vzťah inverzný, pretože zvýšením počtu maliarov by mal pracovný čas skrátiť. Vzťah je nadviazaný;

3 maliari - 5 hodín

4 maliari- X hodín

Ak je vzťah inverzný, poradie prevádzky sa obráti. Toto je správny spôsob;

(3 maliari) . (5 hodín) / 4 maliari = 3,75 hodín

Termín maliari sú zjednodušené a výsledok je 3,75 hodín.

Stav

Aby ste boli v prítomnosti zlúčeniny alebo viacnásobnej proporcionality, je potrebné nájsť tak typy vzťahov medzi veľkosťami a premennými.

- Priamy: Premenná predstavuje rovnaké správanie ako neznáme. To znamená zvýšením alebo znížením jedného, ​​druhý sa mení rovnako.

- Inverzia: Premenná predstavuje správanie antonymov na neznáme. Frakcia, ktorá definuje túto premennú v tabuľke hodnôt, sa musí zvrátiť, aby sa reprezentoval nepriamo proporčný vzťah medzi premenlivými a neznámymi.

Overenie výsledkov

Pri práci so zloženými proporcionmitami je veľmi bežné zamieňať rádium veľkosti, na rozdiel od toho, čo sa deje pri obvyklých výpočtoch pomeru, ktorých povaha je väčšinou priama a rozpustná pomocou jednoduchých troch pravidiel.

Preto je dôležité preskúmať logické poradie výsledkov a overiť koherenciu čísel vyvolaných tromi zloženými pravidlami.

V počiatočnom príklade by táto chyba znamenala získanie 20 v dôsledku toho. To znamená, že 20 ľudí na stiahnutie 15 ton tovaru za 4 hodiny.

Na prvý pohľad sa to nezdá byť šialeným výsledkom, ale nárast o takmer 200% zamestnancov (zo 7 na 20 ľudí) je zvedavý, keď je zvýšenie tovaru 50% a dokonca aj s väčšou dobou času na vykonanie práca.

Môže vám slúžiť: Všeobecná parabola rovnica (príklady a cvičenia)

Týmto spôsobom logické overenie výsledkov predstavuje dôležitý krok tým, že implementuje tri zložené pravidlo.

Odbavenie

Aj keď je základná povaha týkajúca sa matematickej formácie, klírens predstavuje dôležitý krok v prípadoch proporcionality. Chybná vôľa je dostatočná na zneplatnenie akéhokoľvek výsledku získaného v poradí troch jednoduchých alebo zlúčenín.

História

Tri vláda sa stala známym na Západe prostredníctvom Arabov, s publikáciami niekoľkých autorov. Medzi nimi Al-Jwarizmi a Al-Biruni.

Al-Biruni, vďaka svojim multikultúrnym znalostiam, mal prístup k rozsiahlym informáciám o tejto praxi v jeho cestách do Indie, ktorý bol zodpovedný za najrozsiahlejšiu dokumentáciu o troch pravidlách troch.

Vo svojom vyšetrovaní vyvoláva, že India bola prvým miestom, kde bolo použitie týchto troch pravidiel spoločné. Autor uisťuje, že bol plynulý v jeho priamej, inverznej a dokonca zloženej verzii.

Presný dátum, v ktorom sa tri pravidlá stali súčasťou matematických znalostí Indie, je stále známy. Najstarší dokument zameraný na túto prax, Bakhshaliho rukopis, bol však objavený v roku 1881. V súčasnosti je v Oxforde.

Mnoho historikov matematiky zabezpečuje, že tento rukopis pochádza od začiatku súčasnej éry.

Vyriešené cvičenia

Cvičenie 1

Letecká spoločnosť sa musí presunúť 1535 ľudí. Je známe, že s 3 lietadlami by trvalo 12 dní, kým by sa dal posledný cestujúci na miesto určenia. 450 ďalších ľudí dosiahlo leteckú spoločnosť a 2 lietadlá sú nariadené, aby s touto úlohou spolupracovali. Koľko dní bude letecká spoločnosť za posledným cestujúcim do svojho cieľa?

Vzťah medzi počtom ľudí a dňami práce je priamy, pretože čím viac ľudí, bude na vykonanie tejto práce povinní viac dní, bude potrebných viac dní.

Na druhej strane, vzťah medzi lietadlami a dňami je nepriamo úmerný. Zvýšením množstva lietadiel sa potrebné dni znížia na prenos všetkých cestujúcich.

Tabuľka hodnôt týkajúcich sa tohto prípadu sa vykonáva.

Ako je uvedené v počiatočnom príklade, čitateľ a menovateľ sa musia investovať do frakcie zodpovedajúcej reverznej premennej vzhľadom na neznáme. Opúšťanie operácie takto:

Môže vám slúžiť: výpočet prístupov pomocou diferenciálov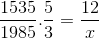

X = 71460/7675 = 9,31 dní

Ak chcete prejsť na 1985 ľudí, ktorí používajú 5 lietadiel, je potrebných viac ako 9 dní.

Cvičenie 2

Zber kukurice s 25 -kameňom sa odberie na nákladné autá nákladných vozidiel. Je známe, že predchádzajúci rok trval 8 hodín s výplatou 150 pracovníkov. Ak sa tento rok mzdy zvýši o 35%, ako dlho bude trvať, kým sa naplní nákladné vozidlá na záťaž 40 -kamienkovou úrodou?

Predtým, ako predstavuje tabuľku hodnôt, musí byť definovaný počet pracovníkov pre tento rok. To zvýšilo 35% počiatočného čísla 150 pracovníkov. Na tento účel sa používa priame tri pravidlo.

100% - 150

35% - x

X = (35 . 100)/100 = 52,5. Toto je počet ďalších pracovníkov v súvislosti s predchádzajúcim rokom, ktorý získa celkový počet 203 pracovníkov, nešťastných, aby zaokrúhlil získanú sumu.

Je definovaná zodpovedajúca tabuľka údajov

V tomto prípade hmotnosť predstavuje priamu vzťahovú premennú s neznámym časom. Na druhej strane premenná pracovníkov spravuje inverzný vzťah s časom. Väčší počet pracovníkov, deň bude kratší.

Berúc do úvahy tieto úvahy a investovanie frakcie zodpovedajúcej pracovníkom sa vypočíta.

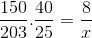
X = 40600 /6000 = 6,76 hodín

Deň bude trvať o niečo menej ako 7 hodín.

Navrhované cvičenia

- Definujte 73% z 2875.

- Vypočítajte množstvo hodín, ktoré Teresa spí, ak je známe, že iba 7% z celkového denného spánku. Definujte, koľko hodín spí týždenne.

- Verejné noviny z roku 2000 každých 5 hodín, používajúc iba 2 tlačové stroje. Koľko kópií bude produkovať za 1 hodinu, ak použijete 7 strojov? Ako dlho bude produkovať 10.000 kópií pomocou 4 strojov?

Odkazy

1. Encyklopédia Alvarez-inciacion. Do. Álvarez, Antonio Álvarez Pérez. Edaf, 2001.
2. Kompletný elementárny a vynikajúci primárny návod na príručku: na použitie uchádzačov pre učiteľov a najmä študentov normálnych provinčných škôl, zväzok 1. Joaquín Avendaño. Tlač d. Dionisio Hidalgo, 1844.
3. Hodnotenie aproximácie skutočných funkcií. P. P. Petrushev, Vasil Atanasov Popov. Cambridge University Press, 3. marca. 2011.
4. Elementárna aritmetika pre výučbu na školách a školách v Strednej Amerike. Darío González. Tip. Arenales, 1926.
5. Štúdium matematiky: o štúdiu a ťažkostiach matematiky. Augustus de Morgan. Baldwin a Cradock, 1830.