Dôkaz nehnuteľnosti, príklady

Ten Vlastnosť algebra zámku Je to jav, ktorý sa týka dvoch prvkov set s operáciou, ak je potrebná podmienka, že po 2 prvkoch uvedených operácií patrí výsledok aj do počiatočnej sady.

Napríklad, ak sa ako celok berú dokonca aj čísla a súčet ako operácia, získa sa zámok uvedenej sady vzhľadom na sumu. Je to preto, že súčet 2 párnych čísel sa vždy uvedie v dôsledku iného čísla, čím sa splní podmienka zámku.

Zdroj: UNSPASH.com

[TOC]

Charakteristika

Existuje veľa vlastností, ktoré určujú algebraické priestory alebo telá, ako sú štruktúry alebo krúžky. Vlastnosť zámku je však jedným z najznámejších v základnej algebre.

Nie všetky aplikácie týchto vlastností sú založené na javoch alebo numerických prvkoch. Mnoho každodenných príkladov môže fungovať z algebraického teoretického prístupu čisto.

Príkladom môžu byť občania krajiny, ktorí predpokladajú právny vzťah akéhokoľvek druhu, napríklad obchodnú alebo manželskú spoločnosť. Po tejto operácii alebo vedení sú stále občanmi krajiny. Operácie občianstva a riadenia tak teda predstavujú zámok.

Numerická algebra

Pokiaľ ide o čísla, existuje veľa aspektov, ktoré boli dôvodom štúdia v rôznych prúdoch matematiky a algebry. Z týchto štúdií vyplynulo veľké množstvo axiómov a teorémov, ktoré slúžia ako teoretický základ súčasného výskumu a diel.

Ak pracujete s numerickými súbormi, môžeme si vytvoriť ďalšiu platnú definíciu vlastnosti zámku. Hovorí sa, že jedna súprava A je zámok inej sady B, ak A je najmenšia sada, ktorá obsahuje všetky sady a operácie, ktoré domujú B.

Môže vám slúžiť: distribučný majetok

Demonštrácia

Demonštrácia zámku sa aplikuje na prvky a operácie prítomné v súbore skutočných čísel N.

Nech a a b sú dve čísla, ktoré patria do množiny r, zámok týchto prvkov je definovaný pre každú operáciu obsiahnutú v r.

Pridanie

- Súčet: ∀ a ˄ b ∈ R → a + b = c ∈ R

Toto je algebraický spôsob, ako to povedať Pre všetky a a b, ktoré patrí do skutočných čísel, musí byť súčet viac B rovná C, čo tiež patrí k skutočnému.

Je ľahké skontrolovať, či je tento návrh pravdivý; Stačí urobiť sumu medzi akýmkoľvek skutočným číslom a overiť, či výsledok patrí aj do skutočných čísel.

3 + 2 = 5 ∈ R

-2 + (-7) = -9 ∈ R

-3 + 1/3 = -8/3 ∈ R

5/2 + (-2/3) = 11/6 ∈ R

Zistilo sa, že stav zámku je splnený pre skutočné čísla a súčet. Týmto spôsobom sa dá uzavrieť k záveru: Súčet skutočných čísel je algebraický zámok.

Násobenie

- Násobenie: ∀ a ˄ b ∈ R → a . B = c ∈ R

Pre všetky a a b, ktoré patria k skutočným, sa násobenie A for B rovná C, čo tiež patrí k skutočnému.

Pri overení s rovnakými prvkami predchádzajúceho príkladu sa pozorujú nasledujúce výsledky.

3 x 2 = 6 ∈ R

-2 x (-7) = 14 ∈ R

-3 x 1/3 = -1 ∈ R

5/2 x (-2/3) = -5/3 ∈ R

To sú dostatočné dôkazy na to, aby sme dospeli k záveru, že: Násobenie skutočných čísel je algebraický zámok.

Táto definícia je možné rozšíriť na všetky operácie v reálnych číslach, aj keď nájdeme určité výnimky.

Zdroj: Pixabay.com

Špeciálne prípady v r

Rozdelenie

Ako osobitný prípad sa pozoruje rozdelenie, kde sa oceňuje nasledujúca výnimka:

Môže vám slúžiť: Klasická pravdepodobnosť: výpočet, príklady, vyriešené cvičenia

∀ A ˄ B ∈ R → A / B ∉ R ↔ B = 0

Pre všetky a a b, ktoré patria R Musí medzi B nepatrí do reais, ak a iba vtedy, ak sa B rovná nule.

Tento prípad sa vzťahuje na obmedzenie, že nie je schopný rozdeliť medzi nulu. Pretože nula patrí do skutočných čísel, potom sa dospelo k záveru, že: lDivízia nie je zámkom v reálnom.

Rozhlas

Existujú tiež potenciálne operácie, konkrétne vykonávania podania, kde sú prezentované výnimky pre radikálne sily indexu krútiaceho momentu:

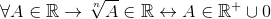; S n par

Za všetko, ku ktorému patrí kráľovskému.

Týmto spôsobom sa označuje, že rovnomerné korene sa vzťahujú iba na pozitívne skutočné a dospelo sa k záveru, že potenciácia nie je zámok v r.

Logaritmus

Je schválený pre logaritmickú funkciu, ktorá nie je definovaná pre hodnoty menšie alebo rovná nule. Skontrolujte, či logaritmus je zámok R, pokračuje nasledovne:

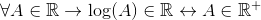
Pre všetko, ku ktorému patrí k reais, logaritmus A patrí k reais, ak a iba vtedy, ak patrí k pozitívnym skutočným.

Ak sú vylúčené záporné a nulové hodnoty, ktoré patria aj k R, možno potvrdiť, že:

Logaritmus nie je zámkom skutočných čísel.

Príklady

Skontrolujte zámok, či neobsahuje súčet a odčítanie prírodných čísel:

Súčet vo n

Prvá vec je skontrolovať podmienku zámku na rôznych prvkoch danej sady, kde ak sa zistí, že niektoré prvky sa zlomia s podmienkou, existencia zámku sa dá automaticky odoprieť.

Môže vám slúžiť: Konvergenčné rádio: Definícia, príklady a cvičenia vyriešené

Táto vlastnosť je splnená pre všetky možné hodnoty A a B, ako je uvedené v nasledujúcich operáciách:

1 + 3 = 4 ∈ N

5 + 7 = 12 ∈ N

1000 + 10000 = 11000 ∈ N

Neexistujú žiadne prirodzené hodnoty, ktoré by zlomili podmienku zámku, takže sa dospelo k záveru:

Súčet je zámok v n.

Odčítanie v n

Hľadá sa prírodné prvky schopné prelomiť stav; A - B patrí domorodcom.

Prevádzku je ľahké nájsť páry prírodných prvkov, ktoré nespĺňajú stav zámku. Napríklad:

7 - 10 = -3 ∉ a n

Týmto spôsobom môžeme dospieť k záveru:

Odčítanie nie je zámkom množiny prírodných čísel.

Navrhované cvičenia

1-prítomný.

2-Vysvetlenie Ak je sada skutočných čísel zámkom celých celých čísel.

3-determina, ktorá numerická sada môže byť zámok reálnych čísel.

4 Zložte vlastnosť zámku pre sadu imaginárnych čísel, vzhľadom na súčet, odčítanie, násobenie a delenie.

Odkazy

1. Panoráma čistej matematiky: voľba Bourbakist. Jean Dieudonné. Reverte, 1987.
2. Teória algebraických čísel. Alejandro J. Díaz Barriga, Ana Irene Ramírez, Francisco Tomás. Národná autonómna univerzita v Mexiku, 1975.
3. Lineárna algebra a jej aplikácie. Sandra Ibeth Ochoa García, Eduardo Gutiérrez González.
4. Algebraické štruktúry V: Teória tela. Héctor a. Merklen. Organizácia amerických štátov, generálny sekretariát, 1979.
5. Úvod do komutatívnej algebry. Michael Francis Atiyah, i. G. Macdonald. Reverte, 1973.