NELINEAROVANÉ METÓDY A PROGRAMOVANIE

Ten Nelineárne programovanie Je to proces optimalizácie funkcie, ktorá závisí od niekoľkých nezávislých premenných, ktoré sú zase predmetom obmedzení.

Ak jeden alebo viac obmedzení alebo ak funkcia maximalizovať alebo minimalizovať (nazývané Objektívna funkcia), nie je vyjadrená ako lineárna kombinácia premenných, takže existuje nelineárny problém s programovaním.

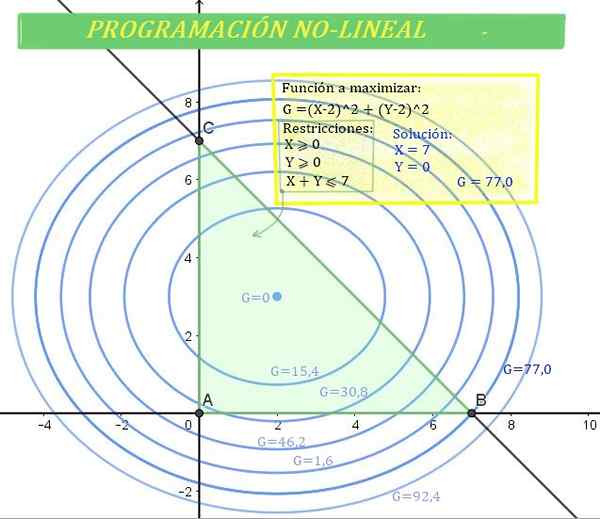
postava 1. Non -lineárny problém s programovaním (NLP). v ktorej g je funkcia (nelineárna) na optimalizáciu v zelenej oblasti, určená obmedzeniami. Zdroj: f. Zapata.

A preto nie je možné použiť postupy a metódy lineárneho programovania.

Napríklad nie je možné použiť dobre známu metódu Jednoduchý, čo sa uplatňuje iba vtedy, keď objektívna funkcia a obmedzenia sú lineárnou kombináciou premenných problému.

[TOC]

Metódy lineárneho programovania

Pre nelineárne programovanie sa hlavné metódy, ktoré sa majú použiť, sú: 

1.- Grafické metódy.

2.- Lagrange multiplikátory na preskúmanie hranice oblasti roztoku.

3.- Výpočet gradientu na preskúmanie koncov objektívnej funkcie.

4.- Metóda zostupných krokov, aby ste našli body nulového gradientu.

5.- Modifikovaná metóda multiplikátorov Lagrange (so stavom Karush-Kuhn-Tucker).

Príklad riešenia s grafickou metódou

Príkladom riešenia s grafickou metódou je to, čo je možné vidieť na obrázku 2:

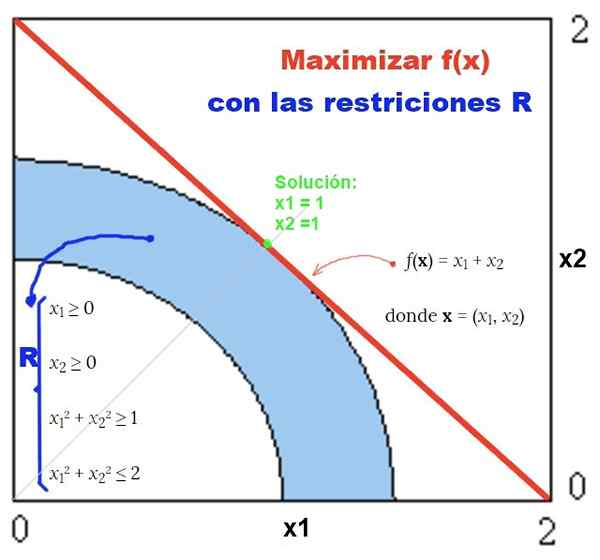Obrázok 2. Príklad nelineárneho problému s nelineárnymi obmedzeniami a jeho grafickým riešením. Zdroj: f. Zapata.

Cvičenia

- Cvičenie 1 (grafická metóda)

Zisk g určitej spoločnosti závisí od sumy predanej produktu X a sumy predaného produktu a navyše je zisk určený nasledujúcim vzorec:

Môže vám slúžiť: konjugovaný binomický: ako je vyriešený, príklady, cvičenia

G = 2 (x - 2)² + 3 (a - 3)²

Je známe, že sumy X a Y majú nasledujúce obmedzenia:

X≥0; Y≥0 a x + a ≤ 7

Stanovte hodnoty x a y, ktoré vytvárajú maximálny zisk.

Obrázok 3. Zisk spoločnosti môže byť matematicky modelovaný tak, aby našiel maximálny zisk nelineárnym programovaním. Zdroj: Pixabay.

Riešenie 

V tomto probléme je objektívna funkcia nelineárna, zatiaľ čo nerovnosti, ktoré definujú obmedzenia. Je to problém Nelineárne programovanie.

Pre riešenie tohto problému bude zvolená grafická metóda.

Po prvé, bude určená oblasť roztoku, ktorá je daná obmedzeniami.

Ako X≥0; Y≥0, riešenie musí hľadať v prvom kvadrante roviny XY, ale navyše je potrebné splniť, že x + y ≤ 7 je roztok v dolnom semiféne riadku x + y = 7.

Oblasť roztoku je priesečník prvého kvadrantu s dolným semiflárom čiary, ktorá vedie k trojuholníkovej oblasti, kde sa nachádza roztok. Je to isté, ako je uvedené na obrázku 1.

Na druhej strane, zisk G môže byť tiež zastúpený v karteziánskej rovine, pretože jej rovnica je rovnica elipsy so stredom (2,3).

Elipsa je znázornená na obrázku 1 pre niekoľko hodnôt G. Vyššia hodnota G, väčší zisk.

Existujú riešenia, ktoré patria do regiónu, ale nedávajú maximálnu hodnotu G, zatiaľ čo iné, napríklad G = 92.4, sú mimo zelenej zóny, to znamená zóna roztoku.

Potom maximálna hodnota g, takže x e y patrí do oblasti riešenia, zodpovedá: 

Môže vám slúžiť: teoretická pravdepodobnosť: ako to dostať von, príklady, cvičenia

G = 77 (maximálny zisk), ktorý sa vyskytuje pre x = 7 e y = 0. 

Je zaujímavé, že maximálny zisk nastane, keď je výška predaja produktu a je neplatná, zatiaľ čo množstvo produktu X dosahuje svoju najväčšiu možnú hodnotu.

- Cvičenie 2 (Analytická metóda: Lagrange multiplikátory) 

Nájdite riešenie (x, y), vďaka ktorému je funkcia f (x, y) = x² + 2 a² byť maximum v oblasti g (x, y) = x² + a² - 1 = 0.

Riešenie

Je to jednoznačne nelineárny problém s programovaním, pretože objektívna funkcia F (x, y) a obmedzenie G (x, y) = 0, nie sú lineárnou kombináciou premenných x a y.

Použije sa metóda multiplikátorov Lagrange, ktorá najprv vyžaduje definovanie funkcie Lagrange L (x, y, λ):

L (x, y, λ) = f (x, y) - λ g (x, y) = x² + 2 a² - λ (x² + a² - 1) 

Kde λ je parameter nazývaný Multiplikátor Lagrange.

Na určenie extrémnych hodnôt objektívnej funkcie F, v oblasti roztoku danej obmedzením G (x, y) = 0, sa tieto kroky dodržiavajú:

-Nájdite čiastočné deriváty funkcie Lagrange L, vzhľadom na x, y, λ.

-Nula každý derivát.

Tu sekvencia týchto operácií:

1. ∂L/∂x = 2x - 2λx = 0
2. ∂L/∂y = 4y - 2λy = 0
3. ∂L/∂λ = -(x² + a² - 1) = 0

Možné systémové riešenia

Možným riešením tohto systému je λ = 1 na uspokojenie prvej rovnice, v takom prípade y = 0 na splnenie druhého.

Toto riešenie naznačuje, že x = 1 alebo x = -1, takže je splnená tretia rovnica. Týmto spôsobom boli získané dve roztoky S1 a S2:

S1: (x = 1, y = 0)

S2: (x = -1, y = 0).

Druhou alternatívou je, že λ = 2, aby bola splnená druhá rovnica, bez ohľadu na hodnotu a.

Môže vám slúžiť: Fermat Limit: Čo pozostáva a cvičí vyriešené

V tomto prípade je jediný spôsob, ako je splnenie prvej rovnice, x = 0. Vzhľadom na tretiu rovnicu existujú iba dve možné riešenia, ktoré nazývame S3 a S4:

S3: (x = 0, y = 1)

S4: (x = 0, y = -1)

Ak chcete vedieť, ktoré alebo ktoré z týchto riešení maximalizujú funkciu objektívu, pokračujte v nahradení F (x, y):

S1: f (1, 0) = 1² + 2.0² = 1

S2: f (-1, 0) = (-1)² + 2.0² = 1

S3: f (0, 1) = 0² + 2.1² = 2

S4: f (0, -1) = 0² + dvadsaťjeden)² = 2

Dospeli sme k záveru, že riešenia, ktoré maximalizujú f, keď x a y patria k obvodu g (x, y) = 0, sú s3 a s4.

Páry hodnôt (x = 0, y = 1) y (x = 0, y = -1) maximalizovať f (x, y) v oblasti roztoku g (x, y) = 0.

- Cvičenie 3 (null gradient)

Nájdite riešenia (x, y) pre objektívnu funkciu:

f (x, y) = x² + 2 a²

Byť maximum v oblasti g (x, y) = x² + a² - 1 ≤ 0.

Riešenie

Toto cvičenie je podobné cvičeniu 2, ale oblasť roztoku (alebo obmedzenie) sa rozširuje do vnútornej oblasti obvodu g (x, y) = 0, to znamená k kruhu g (x, y) ≤ 0. To zahŕňa obvod a jeho vnútorný región.

Hraničné riešenie bolo už stanovené v cvičení 2, ale je potrebné preskúmať vnútornú oblasť.

Aby sa to stalo, musí sa vypočítať gradient funkcie F (x, y) a rovná nule, aby sa v oblasti roztoku hľadal extrémne hodnoty v oblasti roztoku. To je ekvivalentné výpočtu čiastočných derivátov F vzhľadom na X a vyrovnanie nuly:

∂f/∂x = 2 x = 0

∂f/∂y = 4 y = 0

Tento systém rovníc má jediné riešenie (x = 0, y = 0), ktoré patrí do kruhu G (x, y) ≤ 0.

Výmena tejto hodnoty vo funkcii F Výsledky:

f (0, 0) = 0

Záverom je, že maximálna hodnota, ktorá preberá funkciu v oblasti roztoku, je 2 a vyskytuje sa na hranici oblasti riešenia, pre hodnoty (x = 0, y = 1) y (x = 0, y = -1).

 Odkazy

1. Avriel, m. 2003. Nelineárne programovanie. Publikovanie Doveru.
2. Bazaraa. 1979. Nelineárne programovanie. John Wiley & Sons.
3. Bertsekas, D. 1999. Nelineárne programovanie: 2. vydanie. Athéna vedecký.
4. Nocedal, J. 1999. Numerická optimalizácia. Springer-Verlag.
5. Wikipedia. Nelineárne programovanie. Obnovené z: je.Wikipedia.com