Krížový produkt

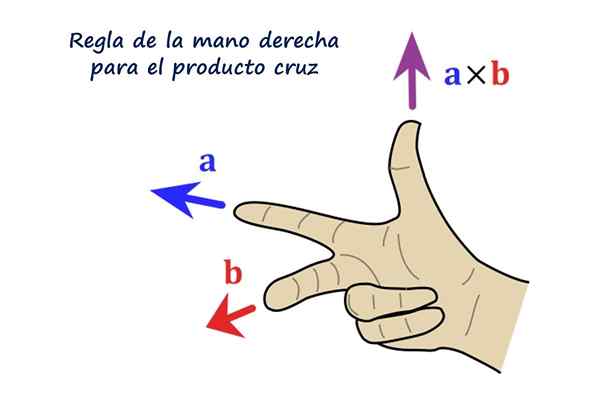
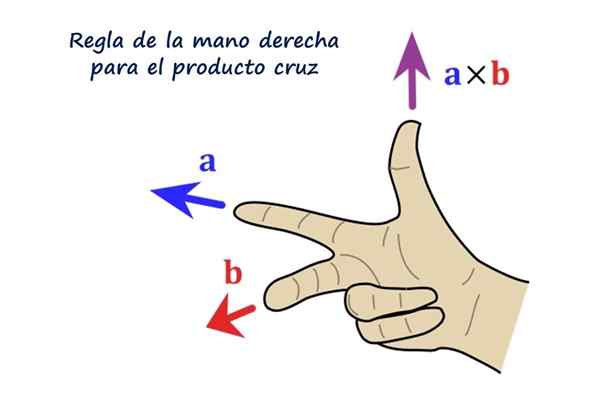Správne pravidlo pre vektorový produkt. Zdroj: f. Zapata.

Aký je prierez alebo vektorový produkt?

On Krížový produkt, Tiež sa nazýva vektorový produkt, je to typ produktu, ktorý sa vykonáva medzi dvoma vektormi a výsledkom je iný vektor, kolmo na rovinu definovanú prvými dvoma.

Krížový produkt medzi akýmikoľvek dvoma vektormi do a b, Výsledkom je ďalší vektor R, Matematicky sa píše takto:

do × b = R

Znie to takto: „Cruz B sa rovná R “.

V tlačenom texte sú vektory napísané s odvážnymi textami alebo so šípkou v liste, aby sa odlíšili od ich veľkosti alebo modulu. Z tohto do Symbol je napísaný takto:

│do│ = a

Absolútna hodnota alebo modul vektora medzi dvoma vektormi sa vypočíta vynásobením modulu oboch vektorov cez uhol 9 medzi nimi:

R = a ∙ b ∙ sen θ

Smer vektora R Je kolmá na vektory do a b. Zmysel R Je to dextrogy do smerom k b A v praxi sa určuje pomocou pravidla pravej ruky, ktoré pozostáva z umiestnenia indexu, média a palca pravej ruky takto:

• Ukazovák je umiestnený podľa vektora do
• S prostredným prstom sleduje vektor b
• Palec, rozšírený, označuje smer a smer vektora R.

Táto objednávka sa musí presne dodržiavať, pretože vektorový produkt nie je komutatívny, to znamená do × b ≠ b × do A ak sa vektory vymieňajú, nedosiahne sa správny výsledok.

Môže vám slúžiť: Existencia a jedinečnosť veta: demonštrácia, príklady a cvičenia

Čitateľovi sa odporúča umiestniť pravú ruku, ako ukazuje obrázok, index smerujúci doľava predstavuje vektor do, Nasleduje prostredný prst b A ukazuje priamo na čitateľa, nakoniec palec označuje hore, ukazuje na smer a smer vektora do × b = R.

Vlastnosti produktu Cruz

-Krížový alebo vektorový produkt medzi dvoma vektormi vždy vedie k inému vektorovi.

-Krížový produkt preto nie je komutatívny: do × b ≠ b × do.

-Pre krížový produkt je pravda, že: do × b = - (b × do). Táto vlastnosť sa volá protivláda.

-Výsledný vektor vektorového produktu medzi dvoma vektormi je kolmý (normálny) na uvedené vektory.

-Z vyššie uvedeného vyplýva, že vektorový produkt medzi vektormi s rovnakým smerom je null. Predovšetkým do × A = 0.

-Krížový produkt je v súlade s distribučným zákonom v súvislosti so sumou: do × (b+c) = do × b + do × c

-Ak je m skalárny, potom m (do × b) = m do × b = do × m b

Krížový produkt medzi jednotkovými vektormi

Tri jednotkové vektory, nazývané Jo, J a klimatizovať, Sú kolmé na seba a označujú tri pozoruhodné smery priestoru: vysoké, široké a hĺbkové. Tieto adresy sú navzájom kolmé.

Vektorový produkt medzi jednotkovými vektormi sa ľahko určí pravou pravou rukou a nezabudnite na vlastnosti krížového produktu:

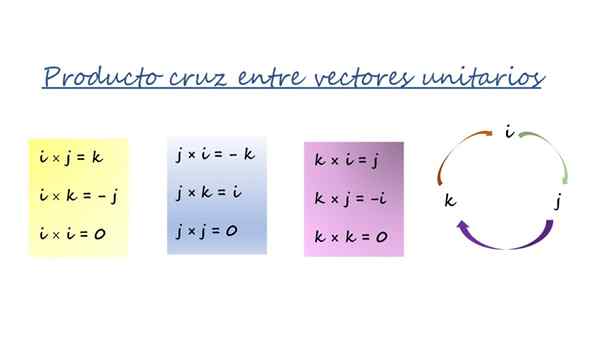Vektorový produkt karteziánskych jednotiek vektorov. Zdroj: f. Zapata.

Tri farebné škatule na obrázku sú zhrnuté v kole so šípkami vpravo a používajú sa týmto spôsobom:

-Pri násobení v smere šípky je výsledkom vektor pred šípkou a má kladné znamenie. Napríklad vynásobením vektora J a klimatizovať, Tretí vektor je Jo, A keďže objednávka sleduje význam šípky, znakom je +.

Môže vám slúžiť: vektorové funkcie

-A ak sa vynásobí v opačnom smere ako šípka, výsledkom je tretí vektor pred šípkou, ale so záporným znakom.

Jednotkové vektory tvoria základňu, takže akýkoľvek iný vektor môže byť napísaný z hľadiska nich. To výrazne uľahčuje výpočet krížového produktu medzi dvoma ľubovoľnými vektormi vo vesmíre.

Ako analyzovať prierezový produkt dvoch vektorov analyticky

Keď vektory do a b Majú ľubovoľný smer vo vesmíre, s komponentmi pozdĺž každého z nich je ľahšie vypočítať krížový produkt analytickým spôsobom a vyjadriť ich z hľadiska jednotkových vektorov Jo, J a klimatizovať:

• do = a_X Jo + do_a J + do_z klimatizovať
• b = b_X Jo + b_a J + b_z klimatizovať

Teraz sa používa distribučná vlastnosť násobenia, ktorá platí aj pre krížový produkt:

do × b = (a_X Jo + do_a J + do_z klimatizovať) × (b_X Jo + b_a J + b_z klimatizovať) =

= (a_X Jo × B_X Jo) + (a_X Jo × B_a J) + (a_X Jo × B_z klimatizovať) + (a_A J × B_X Jo) + (a_A J × B_a J) + (a_A J × B_z klimatizovať) + (a_Z klimatizovať × B_X Jo) + (a_Z klimatizovať × B_a J) + (a_Z klimatizovať × B_z klimatizovať)

Krížové produkty medzi rovnakými jednotkovými vektormi sú zrušené, pretože ide o paralelné vektory, čo tento výraz znižuje na 6 výrazov:

do × b = (a_X Jo × B_a J) + (a_X Jo × B_z klimatizovať) + (a_A J × B_X Jo) + (a_A J × B_z klimatizovať) + (a_Z klimatizovať × B_X Jo) + (a_Z klimatizovať × B_a J)

Nakoniec, pomocou vyššie uvedeného obrázku, každý produkt má za následok:

do × b = a_X b_a klimatizovať + do_X b_z ( -J) + a_A b_X ( -klimatizovať) + a_A b_z Jo + do_Z b_XJ + do_Z b_a ( -Jo) =

= (a_A b_z - a_Z b_a) Jo + (_Z b_X - a_X b_z) J + (_X b_a - a_A b_X) klimatizovať

Cruz produkt prostredníctvom determinantu

Nie je potrebné si zapamätať vyššie uvedený vzorec, ale pohodlne aplikovať kolo predchádzajúcej postavy alebo jednoducho starostlivo vykonávať determinant uvedený nižšie, čo je úplne rovnocenné:

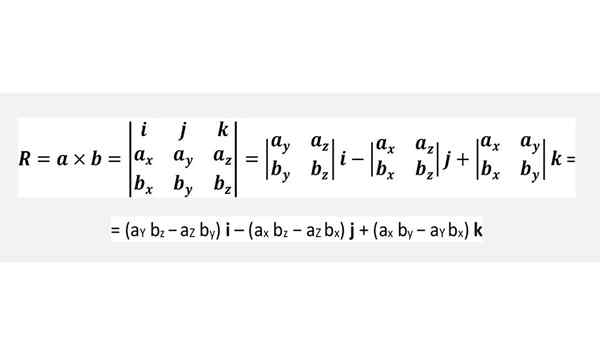
Príklad

Za predpokladu vektorov do a b sú:

• do = 5 Jo - J + 4 klimatizovať
• b = -Jo + 0J +7 klimatizovať

Krížový produkt medzi nimi sa vypočíta identifikáciou a výmenou príslušných súradníc:

Môže vám slúžiť: Hyperbolický paraboloid: Definícia, vlastnosti a príklady

do_X = 5; do_a = −1; do_z = 4; b_X = −1; b_a = 0: b_z = 7

do × b = [(−1) ∙ 7 - 4 ∙ 0] Jo + [(4 ∙ (−1) - 5 ∙ 7) J + [5 ∙ 0 - (−1) ∙ (−1)] klimatizovať = [−7 - 0] Jo + [(-4 - 35) J + [0 - 1] klimatizovať =

= (−7) Jo - 39 J - klimatizovať

Determinantovacia metóda ponúka rovnaký výsledok.

Cvičenie

Vypočítajte determinantami, krížový produkt medzi vektormi:

• alebo = 2 Jo +J + 5 klimatizovať
• vložka = Jo + 4J +7 klimatizovať

A určte plochu rovnobežníka, ktorý je vylúčený predchádzajúcimi vektormi, ako je to znázornené na obrázku:

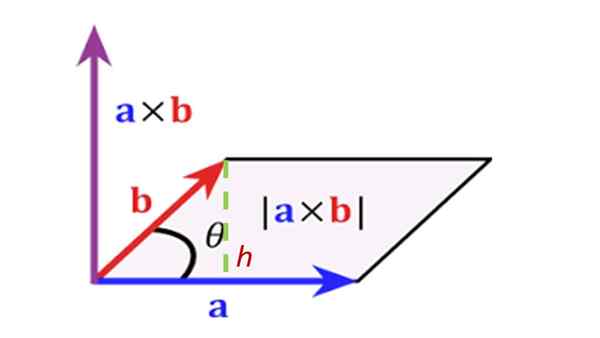
Riešenie

Hodnoty súradníc vektorov sa v determinante nahradia:

Určená plocha rovnobežníka je modul vektorového produktu medzi nimi, čo je výsledkom: R = 17,3 jednotiek oblasti.