Podmienená pravdepodobnosť vzorec a rovnice, vlastnosti, príklady

Ten podmienečná pravdepodobnosť Je to možnosť výskytu určitej udalosti, pretože iná sa vyskytuje ako podmienka. Tieto ďalšie informácie môžu upraviť (alebo možno nie) vnímanie, že sa niečo stane.

Môžeme sa napríklad opýtať sami seba: „Aká je pravdepodobnosť, že dnes prší, pretože pred dvoma dňami neprší?„. Udalosť, o ktorej chceme poznať pravdepodobnosť, že dnes prší, a ďalšie informácie, ktoré by podmienili odpoveď, je, že „pred dvoma dňami neprší“.

postava 1. Pravdepodobnosť, že dnes prší, pretože včera pršalo, je tiež príkladom podmienenej pravdepodobnosti. Zdroj: Pixabay.

Byť Pravdepodobnostný priestor zložené z co (vzorový priestor), ℬ (náhodné udalosti) a P (pravdepodobnosť každej udalosti), plus udalosti A a B, ktoré patria do ℬ.

Podmieňovaná pravdepodobnosť, ktorá sa vyskytuje, pretože B, ktorý je označený ako p (a│b), je definovaný týmto spôsobom:

P (a│b) = p (a∩b) / p (b) = p (a a b) / p (b)

Kde: p (a) je pravdepodobnosť výskytu a, p (b) je pravdepodobnosť udalosti B a je odlišná od 0 a p (a∩b) je pravdepodobnosť priesečníka medzi A a B, to znamená , pravdepodobnosť, že sa vyskytnú obidve udalosti (spoločná pravdepodobnosť).

Toto je výraz pre Bayesovu vetu, ktorá sa uplatňuje na dve udalosti, navrhla v roku 1763 anglický teológ a matematik Thomas Bayes.

[TOC]

Vlastnosti

-Všetka podmienená pravdepodobnosť je medzi 0 a 1:

0 ≤ p (a│b) ≤ 1

-Pravdepodobnosť, že sa udalosť dôjde, pretože k tejto udalosti dôjde, je samozrejme 1:

P (a│a) = p (a∩a) / p (a) = p (a) / p (a) = 1

-Ak sú dve udalosti exkluzívne, tj udalosti, ktoré sa nemôžu vyskytnúť súčasne, potom je to podmienená pravdepodobnosť, že jedna z nich sa stane 0, pretože križovatka je neplatná:

P (a│b) = p (a∩b) / p (b) = 0 / p (b) = 0

-Ak B je podskupina A, potom je podmienená pravdepodobnosť tiež 1:

Môže vám slúžiť: Toroid alebo Toro Dona

P (b│a) = p (a∩b) / p (a) = 1

Dôležitý

P (a│b) sa vo všeobecnosti nerovná P (b│a), preto musíte pri hľadaní podmienečnej pravdepodobnosti postarať sa o výmenu udalostí.

Všeobecné pravidlo násobenia

Mnohokrát chcete nájsť spoločnú pravdepodobnosť p (a∩b), namiesto podmienenej pravdepodobnosti. Takže prostredníctvom nasledujúcej vety máte:

P (a∩b) = p (a a b) = p (a│b). P (b)

Vetu je možné rozšíriť na tri udalosti A, B a C:

P (a∩b∩c) = p (a a b a c) = p (a) · p (b│a) · p (c│a∩b)

A tiež pre niekoľko udalostí, napríklad₁, Do₂, Do₃ A viac, dá sa vyjadriť takto:

P (a₁∩ a₂ ∩ a₃… ∩ A_n) = P (a₁) . P (a₂│A₁). P (a₃│A₁∩ a₂) ... p (a_n│A₁∩ a₂∩ ... a_N-1)

Ak je to prípad udalostí, ktoré sa vyskytujú v poradí a v rôznych štádiách, je vhodné usporiadať údaje v diagrame alebo tabuľke. To uľahčuje vizualizáciu možností na dosiahnutie požadovanej pravdepodobnosti.

Príkladom toho sú stromový diagram a kontingencia. Z jedného z nich si môžete postaviť druhú.

Príklady podmienenej pravdepodobnosti

Pozrime sa na niektoré situácie, v ktorých sa pravdepodobnosť udalosti mení výskytom iného:

- Príklad 1

V sladkom obchode sa predávajú dva typy koláčov: jahoda a čokoláda. Pri registrácii preferencií 50 klientov oboch pohlaví boli stanovené tieto hodnoty:

-27 žien, z ktorých 11 uprednostňuje jahodový a 16 čokoládový koláč.

-23 mužov: 15 čokolády a 8 jahôd.

Pravdepodobnosť, že si zákazník vyberie čokoládový koláč, sa dá určiť použitím pravidla Laplace, podľa ktorej je pravdepodobnosť akejkoľvek udalosti:

P = počet priaznivých udalostí/celkový počet udalostí

V tomto prípade 50 klientov celkom 31 preferuje čokoládu, takže pravdepodobnosť by bola p = 31/50 = 0.62. To znamená, že 62% zákazníkov uprednostňuje čokoládový koláč.

Môže vám slúžiť: polynómové rovnice

Ale bolo by to iné, keby je klient žena? Toto je prípad podmienenej pravdepodobnosti.

Kontingencia

Prostredníctvom takejto pohotovostnej tabuľky sa súčty ľahko vizualizujú:

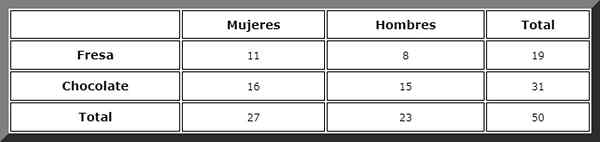
Potom sa pozorujú priaznivé prípady a uplatňuje sa pravidlo Laplace, ale predtým, ako definujeme udalosti:

-B je udalosť „ženský klient“.

-A je udalosť „Preferujte čokoládový koláč“, je žena.

Ideme do stĺpca označeného „žien“ a vidíme, že celková suma je 27.

Potom sa vyhľadáva priaznivý prípad v rade „čokolády“. Existuje 16 udalostí, preto je hľadaná pravdepodobnosť priamo:

P (a│b) = 16/27 = 0.5924

59.24 % žien preferuje čokoládový koláč.

Táto hodnota sa zhoduje, keď kontrastujeme s pôvodne danou definíciou podmienenej pravdepodobnosti:

P (a│b) = p (a∩b) / p (b)

Uisťujeme sa prostredníctvom pravidla Laplace a hodnoty tabuľky:

P (b) = 27/50

P (a a b) = 16/50

Kde p (a a b) je pravdepodobnosť, že klient uprednostňuje čokoládu a je žena. Teraz sa hodnoty vymenia:

P (a│b) = p (a a b)/p (b) = (16/50)/(27/50) = 16/27 = 0.5924.

A je dokázané, že výsledok je rovnaký.

- Príklad 2

V tomto príklade platí pravidlo multiplikácie. Predpokladajme, že na výstave obchodu sú nohavice v troch veľkostiach: malé, stredné a veľké.

V veľa s celkom 24 nohavicami, z ktorých je 8 z každej veľkosti a všetky sú zmiešané. Aká by bola pravdepodobnosť extrahovania dvoch z nich a že obidve boli malé?

Je zrejmé, že pravdepodobnosť extrahovania malých nohavíc pri prvom pokuse je 8/24 = 1/3. Teraz je druhá extrakcia podmienená prvou udalosťou, pretože keď vyberiete nohavice, už nie je 24, ale 23. A ak sú odstránené malé nohavice, namiesto 8 je 7.

Môže vám slúžiť: Multiplikatívny princíp: Techniky počítania a príklady

Udalosť a je vytiahnuť malé nohavice, keď pri prvom pokuse vzal ďalšie. A udalosť B je udalosť malých nohavíc na prvé. Preto:

P (b) = 1/3; P (a│b) = 7/24

Nakoniec prostredníctvom pravidla multiplikácie:

P (a∩b) = (7/24).(1/3) = 7/72 = 0.097

Cvičenie

V štúdii presnosti na komerčných letoch leteckých letov sú k dispozícii tieto údaje:

-P (b) = 0.83, je pravdepodobnosť, že lietadlo vyžaduje včasné.

-P (a) = 0.81, je pravdepodobnosť pristátia včas.

-P (b∩a) = 0.78 Je pravdepodobnosť, že let dorazí včas a bude včasný.

Žiada sa na výpočet:

a) Aká je pravdepodobnosť, že lietadlo pristane okamžite, pretože to vzlietlo včas?

b) Vyššie uvedená pravdepodobnosť je rovnaká ako pravdepodobnosť, že vyšla včas, ak sa vám podarilo okamžite pristáť?

c) A nakoniec: Aká je pravdepodobnosť, že príde včas, pretože to nevyšlo včas?

Obrázok 2. Presmvóda na komerčných letoch je dôležitá, pretože oneskorenia generujú straty milionára. Zdroj: Pixabay.

Roztok

Na zodpovedanie otázky sa použije definícia podmienenej pravdepodobnosti:

P (a│b) = p (a∩b) / p (b) = p (a a b) / p (b) = 0.78/0.83 = 0.9398

Riešenie B

V tomto prípade sa udalosti vymieňajú v definícii:

P (b│a) = p (a∩b) / p (a) = p (a a b) / p (a) = 0.78/0.81 = 0.9630

Všimnite si, že táto pravdepodobnosť sa mierne líši od predchádzajúcej, ako sme už uviedli.

Riešenie c

Pravdepodobnosť, že nebude presné, je 1 - p (b) = 1 - 0,83 = 0.17, budeme to nazvať P (b^C), Pretože je doplnkovou udalosťou na včasné. Požadovaná pravdepodobnosť podmienečnej pravdepodobnosti je:

P (a│b^C) = P (a∩b^C) / P (b^C) = P (a a b^C)/P (b^C)

Na druhej strane:

P (a∩b^C) = P (časové pristátie) - P (časové pristátie a vzlietnutie) = 0.81-0.78 = 0.03

V takom prípade je požadovaná pravdepodobnosť:

P (a│b^C) = 0.03/0.17 = 0.1765

Odkazy

1. Canavos, g. 1988. Pravdepodobnosť a štatistika: Aplikácie a metódy. McGraw Hill.
2. Devore, J. 2012. Pravdepodobnosť a štatistika pre inžinierstvo a vedu. 8. Vydanie. Cengage.
3. Lipschutz, s. 1991. Séria Schaum: Pravdepodobnosť. McGraw Hill.
4. Obregón, i. 1989.Teória pravdepodobnosti. Redakčná limusa.
5. Walpole, r. 2007. Pravdepodobnosť a štatistika pre inžinierstvo a vedu. Pearson.
6. Wikipedia. Podmienečná pravdepodobnosť. Obnovené z: je.Wikipedia.orgán.