Objednaný pár

Čo je to usporiadaný pár?

Usporiadaný pár resp duo Je to súbor dvoch prvkov, ktoré sú napísané podľa objednávky stanoveného určitým kritériom. Uvedené kritériá špecifikujú, ktorý z týchto dvoch prvkov ide ako prvé a ktorý z nich ide po.

Orderovaný pár je označený ako (x, y), kde „x“ je prvým prvkom páru a „y“ je druhý, tiež nazývaný tiež nazývaný Komponenty. Všeobecne (x, y) to nie je rovnaký uprataný krútiaci moment (y, x). A okrem poradia je ďalšou dôležitou charakteristikou usporiadaných párov rovnosť: dva usporiadané páry (a, b) a (c, d) sú rovnaké iba vtedy, ak a = c a b = d.

postava 1.- Vďaka úpravám párov šteniatko vie, že kosti sú pochované na miestach (3,1) a (-4,2), zatiaľ čo jeho dom je v (0,0). Zdroj: f. Zapata.

Príkladmi usporiadaných párov by boli tie, ktoré sú zložené z veku a hmotnosti kurzu študentov matematiky. Orderovaný pár (15, 62) zodpovedá 15 -ročnému študentovi, ktorý sa líši od nepravdepodobného páru (62,15).

Koncept usporiadaného krútiaceho momentu je veľmi dôležitý v rôznych oblastiach matematiky, ako je karteziánska rovina, frakcie, vektory v lietadle, vzťahy a funkcie. Dôležitým aspektom je, že ich prvky nemusia mať nevyhnutne číselné, napríklad ich možno objednať s:

• Krajina
• Meno priezvisko
• Manželka manžel

A mnoho ďalších kombinácií.

Príklady objednaných párov

Zlomky

Frakcia je znázornená ako kvocient dvoch p/q celých čísel, napríklad frakcia ½, čo je ekvivalentné desatinnému číslu 0.5.

Táto frakcia však nie je jediná, ktorá predstavuje desatinné miesto 0.5, tak aj takto:

2/4; 3/6; (-2)/(-4); 20/40; (-1)/(-2)…

Týmto spôsobom môže byť akákoľvek frakcia reprezentovaná ako usporiadaný pár (P, Q), kde sú p a q celé, pričom P zaberá polohu čitateľa a Q polohy menovateľa. Existuje dôležité obmedzenie a že Q (menovateľ) sa musí líšiť od 0, pretože frakcie formulára P/0 nie sú definované.

Môže vám slúžiť: konečná súprava: Vlastnosti, príklady, vyriešené cvičenia

A ďalšou dôležitou podmienkou je, že dve frakcie A/B a C/D sú rovnaké, pokiaľ sa to splní:

A ∙ d = b ∙ c

Funkcie a jeho grafy

Funkciu možno vyjadriť ako sada uprataných párov. Napríklad grafom funkcie v karteziánskej rovine je prvému prvku priradená poloha nezávislej premennej, zatiaľ čo druhej je priradená závislá premenná. Toto je usporiadaný pár.

Pre funkciu y = f (x) možno uprataný krútiaci moment vyjadriť ako [x, f (x)]]. Zvážte napríklad počiatočnú sadu:

A = 1, 2, 3, 4

V tejto sade sú prvé komponenty usporiadaného páru podľa funkcie y = x². Sada druhých komponentov je:

B = 1, 4, 9, 16

A usporiadané páry sú:

(1,1); (2,4); (3, 9); (4; 16)

Hľadať.

Vektory v lietadle

Vektory môžu byť reprezentované v karteziánskej rovine pomocou usporiadaných párov, kde prvý prvok predstavuje horizontálnu komponent „X“ a druhý vertikálny komponent „y“. Na rozlíšenie vektorov od bodov v rovine sú označené výraznými písmenami a namiesto zátvoriek sa používajú štvorcové zátvorky, ako je tento:

vložka =

Napríklad vektor vložka = má horizontálnu komponent rovnú 4 a vertikálne zložku rovnajúcu sa 7. Jeho graf je:

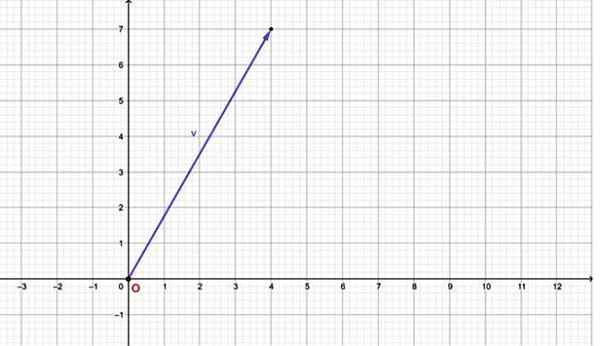Obrázok 2.- Vektor roviny sa môže vyjadriť pomocou usporiadaného páru. Zdroj: f. Zapata.

Všimnite si, že tento vektor má svoj pôvod, ktorý sa zhoduje s pôvodom súradníckeho systému (0,0). Ak má vektor svoj pôvod v akomkoľvek inom bode, môže byť vyjadrený aj vo forme usporiadaného krútiaceho momentu prostredníctvom usporiadaných párov, aby ste tak urobili nasledujúce časti.

Môže vám slúžiť: hierarchia operácií

Objednávacie operácie Pares

Prírastok

Nechajte ciele (a, b) a (c, d) páry (d). Nový krútiaci moment sa získa pomocou svojej sumy podľa:

(a, b)+(c, d) = (a+c, b+d)

Neutrálny prvok

Neutrálnym prvkom pridania usporiadaných párov je krútiaci moment (0,0), pretože keď sa pridáva k usporiadanému páru (a, b), súčet je druhý:

(a, b) + (0,0) = (a, b)

Súčet opaku

Pridaním usporiadaného páru (a, b) s jeho opačným (-a, -b) sa získa usporiadaný krútiaci moment (0,0):

(a, b) + (-a, -b) = (0,0)

Komutativita

Poradie dodatkov nezmení súčet:

(a, b) + (c, d) = (c, d) + (a, b)

Asociativita

Výsledok pridania troch usporiadaných párov sa nezmení, keď je zoskupený na vykonanie operácie:

[(a, b) + (c, d)] + (e, f) = (a, b) + [(c, d) + (e, f)]

Odčítanie usporiadaných párov

Nech sú ciele (a, b) a (c, d), odčítanie sa vykonáva takto:

(a, b)-(c, d) = (a-c, b-d)

Produkt

V produkte existujú dve možnosti: i) vynásobte krútiaci moment usporiadaný konštantou a ii) vynásobte dve (alebo viac) úkryt.

Násobenie konštantou

Nech k je konštanta a riadny krútiaci moment (a, b), produkt medzi konštantou a krútiacim momentom je:

K ∙ (a, b) = (k ∙ a, k ∙ b)

Násobenie usporiadaných párov

Produkt medzi usporiadanými pármi (A, B) a (C, D) sa vykonáva takto:

(a, b) x (c, d) = (ac - bd, bc+ad)

Neutrálny prvok

Neutrálny prvok násobenia je (1,0), pretože vynásobením akéhokoľvek krútiaceho momentu, ktorý je týmto usporiadaný, podľa vyššie uvedeného pravidla násobenia je pôvodný krútiaci moment:

(a, b) x (1,0) = (a - 0, b + 0) = (a, b)

Môže vám slúžiť: Multiplikatívna inverzia: Vysvetlenie, príklady, vyriešené cvičenia

Asociativita

Pretože poradie faktorov nemení produkt, môže byť zoskupený rôznymi spôsobmi, aby sa vynásobil tri alebo viac pidy párov a výsledok je rovnaký:

[(a, b) x (c, d)] x (e, f) = (a, b) x [(c, d) x (e, f)]

Vyriešené cvičenia

Cvičenie 1

Objednali ste si páry (x², X-2) = (16, 2). Čo je hodnota x?

Riešenie

Uplatňovanie rovnosti usporiadaných párov sa získa ako prvé:

X² = 16 ⇒ x₁ = 4, x₂ = -4

Ak chcete vedieť, ktorá z týchto dvoch hodnôt si vyberie, použite:

X-2 = 2

x = 2 + 2 = 4

Preto požadovaná hodnota x je 4.

Cvičenie 2

Vyjadriť ako usporiadaný pár vektor, ktorý prechádza z bodu (1, 3) do bodu (7, 11) a reprezentuje ho graficky.

Riešenie

Byť vložka Prehľadal vektor. Na určenie usporiadaného páru, ktorý ho predstavuje a ktorý obsahuje jeho súradnice, sa v tomto poradí odpočítajú súradnice bodu príchodu a bod pôvodu. Tak:

vložka = = =

Potom je zastúpený vektor vložka ako ten, ktorý prechádza z (1.3) do (7, 11) a zariadenia vložka ktorého pôvod je pripevnený k pôvodu súradníckeho systému (0,0). Ako vidíte, majú rovnaký smer a význam.

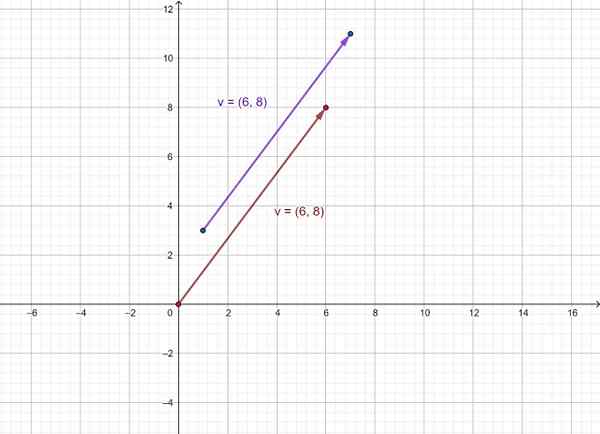Obrázok 3. Zastúpenie vektora ako usporiadaného páru. Zdroj: f. Zapata.

Odkazy

1. Hlboký. Objednaný pár. Získané z: Deepai.orgán.
2. Matematický. Karteziánska reprezentácia vektora pomocou usporiadaného páru. Získané z: Matemovil.com.
3. Rozmanitosť. Objednaný pár. Zdroj: WarsityTorm.com
4. PROSTRI, JUAN. Vzťahy a funkcie. Fakulta inžinierstva. Oddelenie matematiky. Univerzita Buenos Aires. Zdroj: Subjekty.FI.Uba.ar.
5. Denverská univerzita. Vzťahy. Získané z: matematiky.Ucdenver.Edu.