Desatinná poznámka
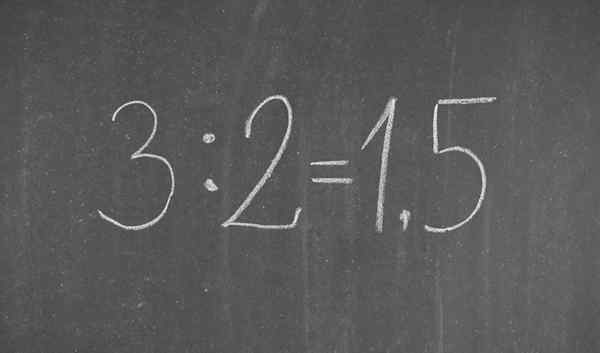
- 1076
- 160
- Tomáš Klapka
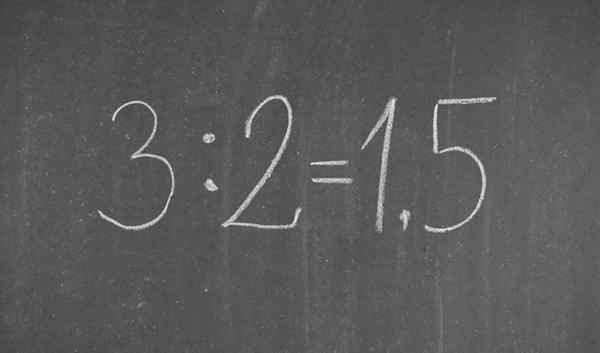 Frakcia 3/2 napísaná v desiatkovom zápise
Frakcia 3/2 napísaná v desiatkovom zápise Čo je desatinné notácie?
Ten desatinná poznámka Spočíva v písaní skutočného čísla prostredníctvom celej časti a desatinnej časti, oddelenej bodom alebo čiarkou. Celá časť je vľavo a desatinná časť napravo od tohto bodu.
0 sa môže objaviť v celej časti, ako aj v desatinnom mieste. Napríklad nasledujúce čísla sú desatinné čísla:
- 0.25
- 1.5903
- 4 19367
Všimnite si, že desatinná časť týchto čísel je konečná, ale existujú aj čísla s nekonečnou desatinnou časťou, ako je 0,33333…, kde sú podozrivé body umiestnené ako spôsob, ako naznačovať, že počet desatinných miest pokračuje neurčito.
Všeobecne platí, že konečné desatinné číslo možno napísať ako:
N.do1do2do3..n
Byť N je celé číslo a n za množstvo desatinných miest, zatiaľ čo nekonečné desatinné miesto prijíma formulár:
N.do1do2do3..
V desatinnom mieste 0.25 je identifikovaných:
- N = 0
- do1 = 2
- do2 = 5
Desatinné miesta vznikajú ako ďalší spôsob vyjadrovania racionálnych čísel, ktoré sú tvarované alebo rozbité. V skutočnosti je možné každú frakciu napísať v desiatkovom zápise, ako bude vidieť okamžite.
Slúžia tiež na reprezentáciu čísel, ktoré nevyvodzujú z zlomku, So -Called iracionálne čísla, ako: π, √2, √3, √5, číslo „E“ a mnoho ďalších.
Príklady desatinných čísel
Decimálne číslo je možné získať z frakcie veľmi jednoduchým spôsobom: výpočet kvocientu čitateľa medzi menovateľom. Ak je menovateľ jednotkou, po ktorej nasledujú nuly, je to veľmi jednoduché:
- 8/10 = 0.8
- - (5/100) = −0.05
V prvom prípade, keď je menovateľ 10, je desatinná čiarka bezprostredne umiestnená vľavo od 8 a desatinné 0.8 znie „8 desatín“ alebo „nulový bod osem“.
V druhom prípade, keďže menovateľ je 100, musíte dať desatinnú čiarku dve miesta vľavo od 5, a keďže číslo je záporné, znie „menej 5 stotiny“ alebo „menej nulového bodu nulového bodu päť“.
Ak menovateľ nie je jednotkou nasledovanou 0, používa sa dlhé rozdelenie:

Všimnite si, že na vykonanie tejto divízie, pretože čitateľ je menší ako menovateľ, bol vynásobený najskôr 10 a pritom 0, nasledovaná desatinnou čiarkou v kvociente, aby nezmenila operáciu, takže nie na zmenu operácie. Potom normálne postupujte rozdeliť 10 o 2, čo sa rovná 5 a zvyšok divízie je 0.
Môže vám slúžiť: vektorové sumyDesatinná forma frakcie ½ je 0.5, číta sa „nulový bod päť“:
Frakcia 7/8 je ďalším príkladom. Keďže 7 je menšie ako 8, vynásobí sa 7 × 10 = 70, A 0 sa umiestni do kvocientu, po ktorom nasleduje desatinná čiarka a je normálne rozdelená:
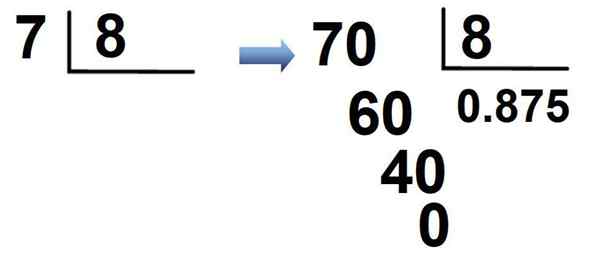
Výsledkom je, že frakcia je napísaná v desiatkovom zápise ako:
7/8 = 0.875
Toto číslo, rovnako ako predchádzajúci výsledok, je konečné desatinné miesto a spôsob jeho čítania je: „nulový bod osemsto stoviek a sedemdesiat -Five“. Prostredníctvom tohto postupu sú nasledujúce frakcie tiež napísané v desiatkovom zápise:
8/10 = 0.8
5/7 = 0.714285714…
9/20 = 0.Štyri. Päť
3/8 = 0.375
Všimnite si, že ako vo všetkých týchto frakciách je čitateľ menší ako menovateľ, celá časť výsledných desatinných miest je 0. Zmiešané číslo alebo a Nesprávny zlomok (Že ktorého čitateľ je väčší ako jeho menovateľ), má tiež desatinné zastúpenie.
V tomto prípade je celá časť väčšia alebo rovná 1, ak je frakcia pozitívna, a menej ako -1, ak je negatívna:
9/4 = 2.25
10/3 = 3.333333…
−12/5 = −2.4
1 ½ = 1.5
2 ¾ = 2.75
Celá časť a frakčná časť negatívnych desatinných miest
V predchádzajúcich príkladoch sa zistilo, že na nájdenie desatinnej expresie frakcie je čitateľ a menovateľ jednoducho rozdelený. Aj keď je frakcia negatívna, jednoducho sa značka mínus dáva do ekvivalentného decimientového výrazu.
Celá časť a frakčná časť desatinného obdobia sa však líšia podľa znaku, ktorý nosíte.
Keď je desatinné desatinné miesto, napríklad 2.25, jeho celá časť je 2 a jej desatinná časť je 0.25 a číslo možno napísať ako súčet celej časti a desatinná časť, ako je táto:
2.25 = 2 + 0.25
Celá časť je definovaná ako celé číslo bezprostredne nižšie ako desatinná časť a desatinná časť je vždy pozitívna. Za 2.25, bezprostredne nižšie celé číslo je 2.
Ale v prípade frakcie −12/5, ekvivalent desatinnej −2.4 Vyššie uvedené nefunguje.
Môže vám slúžiť: Aké sú časti karteziánskeho lietadla?)
−2 + 0.4 = −1.6 ≠ −2.4
Preto celá časť −2.4 nemôže byť −2, ale bezprostredne nižšie celé číslo: −3. Ale v takom prípade by frakčná časť nebola 0.4, pretože pridaním:
-3 + 0.4 = −2.6 ≠ −2.4
Aká je teda desatinná časť záporného čísla −2.4? Odčítava desatinné číslo od celej jeho časti a výsledok bude vždy pozitívny:
−2.4 - ( - 3) = 0.6
Nakoniec sa preukáže, že pridaním celej časti a zlomkovej časti sa získa vyhľadané desatinné miesto:
-3 + 0.6 = −2.4
Postup na nájdenie celej časti a desatinnej časti ľubovoľného čísla, bez ohľadu na znamenie, je zhrnutý týmto spôsobom:
- Celá časť je celé číslo bezprostredne nižšie ako desatinné číslo.
- Desatinná časť sa vypočíta odpočítaním desatinnej časti od celej jeho časti.
Na účely praktického výpočtu však desatinné číslo −2.4 je možné rozdeliť ako - (2 + 0.4) = - 24/10 alebo:
)
Typy desatinných miest
Existujú desatinné čísla, ktorých desatinná časť je konečná alebo nekonečná, ktorá sa používa ako klasifikačné kritériá:
Konečné alebo presné desatinné miesta
Keď sú desatinné desatinné miesta, napríklad 0.125, tiež sa hovorí, že sú presné desatinné miesta.
Nekonečné desatinné miesta
Nekonečné desatinné miesto sa získa, keď sa zvyšok delenia medzi čitateľom a menovateľom nikdy nevykoná 0.
Za predpokladu, že desatinné miesto pochádza z kvocientu medzi dvoma celkovými číslami, táto desatinná časť je pravidelná, to znamená, že sa skladá z jednej alebo niekoľkých čísel, ktoré sa opakujú neurčito, nazývané obdobie.
Napríklad číslo 3.333333… pochádza z nesprávnej frakcie 10/3, je to periodické desatinné miesto: celá časť je 3 a po desatinnej čreve sa číslo 3 opakuje na neurčito. To sa dá symbolizovať umiestnením krivky alebo klobúka na opakované číslo:



Nakoniec existujú nekonečné desatinné miesta, ktoré nie sú novinami, ktoré nepochádzajú z kvocientu medzi dvoma celkovými číslami. Ako je uvedené na začiatku, tieto desatinné miesta patria do celku iracionálne čísla, Napríklad číslo PI, napríklad.
Vyriešené cvičenia
Cvičenie 1
Napíšte numerické nasledujúce desatinné čísla:
a) nulový bod štyri stovky štyridsaťseda
b) päť tisícin
c) dve jednotky a päť stotiny
d) tri body dvadsať -seven negatívny
e) Jeden bod osemsto dvadsaťtisíc päťsto šesťdesiat tri
-
Riešenie
a) 0.447
b) 0.005
c) 2.05
d) −3.27
e) 1.824563
Cvičenie 2
Klasifikujte nasledujúce desatinné čísla v presných desatinných miestach, čistých novinách, zmiešaných novinách alebo iracionálnych číslach. Vo všetkých prípadoch uveďte hodnotu celej časti a ak ide o noviny alebo zmiešané noviny, tiež označujú hodnotu obdobia a podľa potreby prednosť:
a) 0.35627
b) 1,21212121…
c) −1.32
d) 1.414213562… = √2
-
Riešenie
A) 35627 je presná desatinná desatinná desatinná hodnota. Celá jeho časť je 0 a jej desatinná časť je 0.35627.
b) 1.21212121… je nekonečné desatinné a čisté noviny, celá časť je 1 a obdobie je 21.
c) −1.32 je presná a negatívna desatinná desatinná hodnota, ktorej celá časť je −2. Desatinná časť sa vypočíta odpočítaním desatinného čísla od celej časti:
−1.32 - (−2) = 0.68
d) desatinná expresia √2 je nekonečná a nie pravidelná, pretože je to iracionálne číslo.
Je to zmiešané noviny, celá časť je 3, predná je 1 a obdobie je 89.
Odkazy
- Pedagogické príspevky a didaktický materiál. Desatinná poznámka. Získané z: Tecdigital.TEC.Ac.Cr.
- Baldor, a. 2007. Praktický teoretický aritmetický. Redakčná skupina Patria s.Do. c.Vložka.
- Matematika pre obchody. Pochopenie desatinného zápisu. Zdroj: OpenTextBC.Ac.
- Žobrák. Racionálne čísla: významy a reprezentácie. Získané z: Redi.Kódový.Žobrák.mx.



&space;\:&space;3.1\widehat89)