Racionálne čísla Vlastnosti, príklady a operácie

Ten racionálne čísla Sú to všetky čísla, ktoré je možné získať ako rozdelenie dvoch celých čísel. Príklady racionálnych čísel sú: 3/4, 8/5, -16/3 a tie, ktoré sa objavia na nasledujúcom obrázku. V racionálnom čísle je kvocient označený, v prípade potreby je možné to urobiť neskôr.

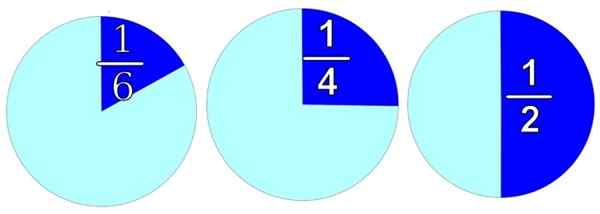
Na obrázku je znázornený akýkoľvek objekt, okrúhly pre pohodlie. Ak ho chceme rozdeliť na 2 rovnaké časti, ako vpravo, máme dve polovice a každá z nich je 1/2.

postava 1. Racionálne čísla sa používajú na rozdelenie celku do rôznych častí. Zdroj: Freesvg.

Rozdeľovaním na 4 rovnaké časti získame 4 kusy a každá má hodnotu 1/4, ako na obrázku stredu. A ak ju musíte distribuovať v 6 rovnakých častiach, potom by každá časť mala 1/6, čo vidíme na obrázku vľavo.

Samozrejme, mohli by sme ho tiež rozdeliť na dve nevýhodné časti, napríklad by sme si mohli ponechať 3/4 dielov a ušetriť 1/4 dielu. Možné sú aj ďalšie divízie, napríklad 4/6 dielov a 2 diely. Dôležité je, že súčet všetkých častí je 1.

Týmto spôsobom je zrejmé, že s racionálnymi číslami môžete rozdeliť, počítať a distribuovať veci ako jedlo, peniaze, pôda a všetky druhy predmetov vo frakciách. A tak sa množstvo operácií, ktoré sa dajú vykonať s číslami, sa predĺži.

Racionálne čísla je možné vyjadriť aj decimálne, ako je zrejmé z nasledujúcich príkladov:

1/2 = 0,5

1/3 = 0,3333…

3/4 = 0,75

1/7 = 0,142857142857142857…

Neskôr uvádzame, ako prejsť z jednej cesty k druhej s príkladmi.

[TOC]

Racionálne čísla Vlastnosti

Racionálne čísla, ktorých set označíme písmenom Q, majú nasledujúce vlastnosti:

-Q Zahŕňa prírodné čísla n a celé čísla n.

Berúc do úvahy akékoľvek číslo do Môže sa vyjadriť ako kvocient medzi sebou a 1, je ľahké vidieť, že existujú aj prírodné čísla a celé čísla.

Prírodné číslo 3 je teda možné napísať ako zlomok a tiež -5:

3 = 3/1

-5 = -5/1 = 5/-1 = -(5/1)

Týmto spôsobom je to číselná sada, ktorá pokrýva väčšie množstvo čísel, niečo veľmi potrebné, vložte čísla „okrúhle“.

Môže vám slúžiť: 90 deliteľov: Čo sú a vysvetlenie

-Racionálne čísla sa môžu pridať, odpočítať, vynásobiť a deliť, výsledkom operácie je racionálne číslo: 1/2 + 1/5 = 7/10; 1/2 - 1/5 = 3/10; (1/2) x (1/5) = 1/10; (1/2) ÷ (1/5) = 5/2.

-Medzi každým niekoľkými racionálnymi číslami je možné vždy nájsť ďalšie racionálne číslo. V skutočnosti medzi dvoma racionálnymi číslami existujú racionálne nekonečné. 

Napríklad medzi racionálnymi 1/4 a 1/2 sú racionálne 3/10, 7/20, 2/5 (a mnoho ďalších), ktoré je možné overiť, že ich vyjadrujú ako desatinné miesta.

-Akékoľvek racionálne číslo možno vyjadriť ako: i) celé číslo alebo ii) obmedzené desatinné miesto (prísne) alebo noviny: 4/2 = 2; 1/4 = 0,25; 1/6 = 0,1666666…

-Rovnaké číslo môže byť reprezentované nekonečnými ekvivalentnými frakciami a všetky patria do Q. Pozrime sa na túto skupinu:

Všetky predstavujú desatinné miesto 0.428571 ..

-Zo všetkých ekvivalentných frakcií, ktoré predstavujú rovnaké číslo, je neredukovateľná frakcia, najjednoduchšia zo všetkých Kanonický zástupca toto číslo. Kanonický zástupca predchádzajúceho príkladu je 3/7.

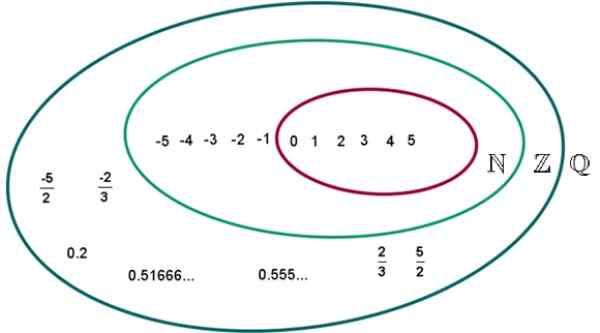Obrázok 2.- Sada Q racionálnych čísel. Zdroj: Wikimedia Commons. UVM Eduardo Artur/CC By-S (https: // creativeCommons.Org/licencie/By-SA/4.0).

Príklady racionálnych čísel

-Vlastné zlomky, tie, v ktorých je čitateľ menší ako menovateľ:

-Nesprávne zlomky, ktorých čitateľ je väčší ako menovateľ:

-Prírodné čísla a celé čísla:

-Rovnocenné frakcie:

Desatinné zastúpenie racionálneho čísla

Keď je čitateľ rozdelený medzi menovateľ, je desatinná forma racionálneho čísla. Napríklad:

2/5 = 0.4

3/8 = 0.375

1/9 = 0.11111 ..

6/11 = 0.545454…

V prvých dvoch príkladoch je množstvo desatinných miest obmedzené. To znamená, že keď je rozdelenie vytvorené, získa sa odpočinok.

Na druhej strane, v nasledujúcich dvoch, počet desatinných miest je nekonečný. V druhom prípade existuje vzor v desatinných miestach. V prípade frakcie 1/9 sa obrázok 1 opakuje neurčito, zatiaľ čo v 6/11 je 54.

Môže vám slúžiť: Pravdepodobnosť frekvencie: koncept, ako sa vypočíta a príklady

Keď sa to stane, hovorí sa, že desatinné noviny sú noviny a sú označené obvodovým prízvukom takto:

Transformovať desatinné na zlomok

Ak je to obmedzené desatinné miesto, čiarka je jednoducho eliminovaná a menovateľ sa stane jednotkou, po ktorej nasleduje toľko nulov, koľko čísel má desatinné miesto. Napríklad na transformáciu desatinných miest 1.26 Frakcia je napísaná takto:

1.26 = 126/100

Potom je výsledná frakcia zjednodulá na maximum:

126/100 = 63/50

Ak je desatinné miesto neobmedzené, najskôr je identifikované obdobie. Potom sa tieto kroky dodržiavajú, aby ste našli výslednú frakciu:

-Čitateľ je odčítanie medzi číslom (bez prízvuku Comma alebo Circomflex) a časťou, ktorá nenesie obvodový prízvuk.

-Menovateľ je celé číslo s toľko 9, koľko čísel je pod obvodom a toľko alebo ako čísla v desatinnej časti nie sú pod obvodom.

Postupujte podľa tohto postupu na transformáciu desatinného čísla 0,428428428 ... v zlomku.

-Prvé je identifikované obdobie, ktoré je opakovanou sekvenciou: 428.

-Potom sa vykonáva prevádzka odpočítania čísla bez kómy alebo prízvuku: 0428 časti, ktorá nemá žiadne obvody, čo je 0. Toto je 428 - 0 = 428.

-Menovateľ je postavený s vedomím, že pod obvodom sú 3 obrázky a všetky sú pod obvodom. Preto je menovateľ 999.

-Nakoniec je frakcia vytvorená a zjednodušená, ak je to možné:

0.428 = 428/999

Nie je možné viac zjednodušiť.

Operácie s racionálnymi číslami

- Pridať a odčítať

Zlomky s rovnakým menovateľom

Ak majú frakcie toho istého menovateľa, pridajte ich a/alebo ich odpočítať, je veľmi ľahké, pretože čitatelia sú jednoducho pridané algebraicky, pričom ako menovateľ výsledku je k tomu isté z dodatkov. Nakoniec, ak je to možné, je to zjednodušené.

Príklad

Vykonajte nasledujúci algebraický súčet a zjednodušte výsledok:

Výsledná frakcia je už neredukovateľná.

Zlomky s rôznym menovateľom

V tomto prípade sú doplnky nahradené ekvivalentnými frakciami s rovnakým menovateľom a potom je už opísaný postup. 

Príklad

Algebraicky pridajte nasledujúce racionálne čísla zjednodušujúce výsledok:

Môže vám slúžiť: okraje kocky

Kroky sú:

-Stanovte minimálny spoločný násobok (MCM) menovateľov 5, 8 a 3:

MCM (5,8,3) = 120

Toto bude menovateľ výslednej frakcie bez zjednodušenia.

-Pre každú frakciu: Rozdeľte MCM medzi menovateľ a vynásobte čitateľom. Výsledok tejto operácie je umiestnený s jej príslušným znakom v frakčnom čitateľovi. Týmto spôsobom sa získa frakcia ekvivalentná originálu, ale s MCM ako menovateľom.

Napríklad pre prvú frakciu je čitateľ postavený takto: (120/5) x 4 = 96 a získa sa:

Pokračujte rovnakým spôsobom pre zostávajúce frakcie:

Nakoniec sa ekvivalentné frakcie nahradia bez toho, aby zabudli na ich znamenie a algebraický súčet čitateľov sa vytvorí:

(4/5) + (14/8) - (11/3) + 2 = (96/120) + (210/120) - (440/120) + (240/120) = =

= (96+210-440+24) / 120 = -110 / 120 = -11/12

- Násobenie

Násobenie a rozdelenie sa vykonáva podľa pravidiel uvedených nižšie:

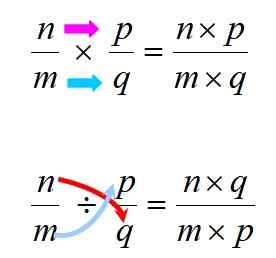Obrázok 3. Pravidlá na vykonávanie znásobenia a rozdelenia racionálnych čísel. Zdroj: f. Zapata.

V každom prípade je dôležité si uvedomiť, že násobenie je komutatívne, čo znamená, že poradie faktorov nemení produkt. Pri divízii sa tak nestane, takže musíte postarať o rešpektovanie príkazu medzi dividend a deliteľ.

Príklad 1

Vykonajte nasledujúce operácie a zjednodušte výsledok:

a) (5/3) x (8/15)

b) (-4/5) ÷ (2/9)

Odpovedať

(5/3) x (8/15) = (5 x 8)/(3 x 15) = 15/120 = 1/8

Odpoveď B

(-4/5) ÷ (2/9) = (-4 x 9)/(5 x 2) = -36/10 = -18/5

Príklad 2     

Luisa mala 45 dolárov. Strávil desiaty nákupom knihy a 2/5 častí toho, čo zostalo v košeli. Koľko peňazí zostane Luisa? Vyjadriť výsledok v neredukovateľnej frakcii.

Riešenie

Cena knihy (1/10) x 45 $ = 0.1 x 45 $ = 4.5 $

Preto Luisa zostala s:

45 - 4.5 $ = 40.5 $

S týmito peniazmi Luisa odišla do obchodu s oblečením a kúpila košeľu, ktorej cena je:

(2/5) x 40.5 $ = 16.2 $

Teraz má Luisa v portfóliu:

40.5 - 16.2 $ = 24.3 $

Ak chcete vyjadriť zlomok, je napísané takto:

24.3 = 243/10

To je neredukovateľné.

Odkazy

1. Baldor, a. 1986. Aritmetika. Vydania a distribúcie Codex.
2. Carena, m. 2019. Matematická príručka. Národná univerzita pobrežia.
3. Figuera, J. 2000. Matematika 8. Edície Co-Bo.
4. Jiménez, r. 2008. Algebra. Sála.
5. Racionálne čísla. Získané z: CIMANET.Uoc.Edu.
6. Racionálne čísla. Zdroj: WebDelprofesor.Ula.ísť.