Koncepcia záporných čísel, príklady, operácie

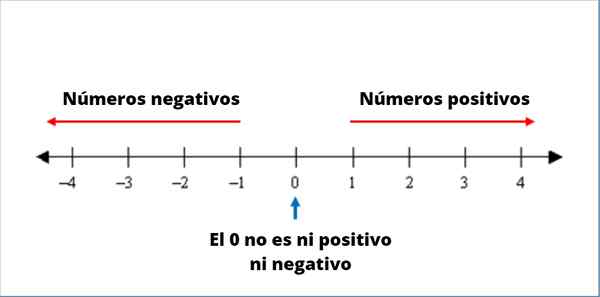
Ten záporné čísla Sú tí, ktorí naľavo od numerickej čiary, vždy predchádzajúce znamenie -. Prostredníctvom negatívov je možné reprezentovať množstvá, ktoré sú pod alebo vľavo z 0.

Tieto čísla sa aktívne zúčastňujú na každodennom živote: Napríklad, ak má niekto dlh 5 dolárov, ale môže platiť iba 3 doláre, dlhuje 2 USD. Dlh je označený negatívnym znakom, ktorý ho odlíši od vyplatenej sumy.

postava 1. Schéma negatívnych a pozitívnych čísel

Polohy nízkej hladiny mora, teploty pod bodom mrazu vody a podlahy nižšie ako úroveň ulíc môžu byť označené zápornými číslami.

[TOC]

Na čo sú záporné čísla pre?

Existencia negatívov rozširuje možné číselné operácie. Uveďme príklad odčítania dvoch čísel. Ak tieto čísla patria domorodcom 1, 2, 3, 4, 5 ... Odčítanie má zmysel iba vtedy, ak sa to robí odpočítaním iného čísla menej ako on.

Výsledok operácie 10 - 7 = 3 je primeraný, pretože v zásade nemôžeme odobrať viac sumy, ako predstavuje.

Avšak s negatívami by sa táto iná situácia opísala dobre: ​​chceme si kúpiť niečo, čo má hodnotu 20 dolárov, ale máme iba 15 dolárov a požiadali sme o 5 dolárov priateľovi. Dlh, ako sme už povedali, je označený negatívnym znamením, a teda 15 - 20 = -5, ktorý sa číta ako „menej 5“.

Sada záporných celých čísel spojených so sadou domorodcov a 0, tvoria najširšiu sadu celých čísel z.

Negatívy však môžu byť tiež frakčné alebo desatinné a patria k ešte širšiemu súboru: skutočné čísla R, ktoré zahŕňa racionálne a iracionálne.

So všetkými z nich sa vykonávajú známe aritmetické operácie, ktoré sa starajú o prevádzku podľa pravidiel jednoduchých znakov, ktoré sú vysvetlené nižšie.

Operácie s zápornými číslami

Pred vykonaním operácií s zápornými číslami musíte vytvoriť niekoľko jednoduchých pravidiel na zvládnutie značky (-), ktoré je potrebné vždy predložiť a poradie čísel.

Môže vám slúžiť: rozdiel medzi spoločnou frakciou a desatinným číslom

Zoberme si číselnú čiaru zobrazenú na obrázku, s negatívmi vľavo od 0 a pozitívnymi vpravo.

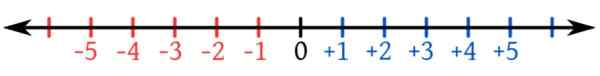Obrázok 2. Numerická čiara s negatívmi v červenej farbe. Zdroj: Wikimedia Commons.

Šípky numerickej čiary v oboch smeroch naznačujú, že existujú nekonečné čísla. Tiež si všimnite, že numerická sada celých čísel je usporiadaná sada a akékoľvek záporné číslo je menšie ako 0 a že akékoľvek pozitívne.

-4 je teda menšia ako 1 a -540 je napríklad menšia ako 84.

Absolútna hodnota

Vzdialenosť medzi ľubovoľným číslom a 0 sa volá absolútna hodnota. Táto vzdialenosť je vždy pozitívna a týmto spôsobom označuje vertikálne tyče:

│-5│ = 5

│+√6│ = √6

│-3/4│ = 3/4

│-10.2│ = 10.2

To znamená, že absolútna hodnota ľubovoľného čísla, či už kladné alebo záporné je kladné číslo čísla. Tento koncept nám bude slúžiť neskôr pri prevádzke s zápornými číslami.

Znak

Ďalším veľmi dôležitým detailom je rozdiel medzi znakom čísla a znakom operácie.

Ak je číslo pozitívne, počet čísla sa zvyčajne vynechá a je zrejmé, že je to aj tak pozitívne, ale s negatívami, ktoré nie sú možné, je preto potrebné používať zátvorky, pozrime sa:

-Správne: 17 - (-6) alebo tiež +17 - (-6)

-Nesprávne: 17 - -6

-Nesprávne: -5 + +7

-Správne: - 5 + (+7) alebo tiež -5 + 7

Keď sú koncepty absolútnej hodnoty, poradie a dôležitosti negatívneho znaku jasné, môžeme sa presunúť na základné operácie.

Prírastok

Rozlišujeme nasledujúce prípady, počnúc súčtom dvoch pozitív, ktorých postup je už veľmi známy:

-Pridajte dve kladné čísla: ( + a) + ( + b) = a + b

Čo znamená, že pridávame ako obvykle, pozrime sa:

(+8) + (+5) = 8 + 5 = 13

-Pridajte dve záporné čísla: (-a) + (-b) =-(a + b)

V tomto prípade pridávame absolútne hodnoty čísel a k výsledku sa predloží negatívny znak, ako je tento:

Môže vám slúžiť: typy integrálov

(-7) + (-11) = - (7+ 11) = - 18

-Pridajte negatívnu a pozitívnu: ( + a) + (-b)

Pre túto operáciu sa odpočítajú absolútne hodnoty a výsledok nesie znak čísla s najvyššou absolútnou hodnotou. Urobme niekoľko prípadov:

a) (-16) + (+3)

Príslušné absolútne hodnoty sú 16 a 3, číslo s najvyššou absolútnou hodnotou je 16, ktorých znamenie je záporné, potom:

(-16) + (+3) = - (16 - 3) = -13

b) (+8) + (-3) = + (8-3) = +5 = 5

Súčet negatív je tiež komutatívny, čo znamená, že poradie v reklamách nie je pre výsledok dôležité.

Predchádzajúce pravidlá sa uplatňujú, ak chcete pridať viac ako dve čísla, ktoré sa dajú vykonať pomocou asociatívnej vlastnosti: a + b + c = (a + b) + c = a + (b + c).

Predtým, ako uvidíme príklad v tomto prípade, pozrime sa najskôr odčítanie dvoch celých čísel.

Odčítanie

Odčítanie je definované ako súčet opakovania. Opak čísla A je -a, ako je tento:

-4 je opak + 4

½ je opak -½

Ak nás požiadajú, aby sme vykonali odčítanie dvoch čísel, bez ohľadu na znamenie, jednoducho pridáme opak druhého:

a) (-53) -(+8) = (-53)+( -8) = -(53+8) = -61

b) (+7) - (-12) = (+7)+(+12) = 7+12 = 19

c) (+2) - (+π) = (+2)+( - π) = 2 - π

Príklad

Vykonajte nasledujúcu operáciu (+4) + (-7) + (+19)

Takto to prepíšeme pomocou štvorcových zátvoriek, aby sme označili operáciu, ktorá sa má vykonať ako prvá:

(+4) + (-7) + (+19) = [(+4) + (-7)] + (+19) = [-(4 -7)] + 19 = [-(-3)] + 19 = 19 - (-3) = 19 + (+3) = 22

Násobenie

Pravidlo znakov pre násobenie je zhrnuté na nasledujúcom obrázku:

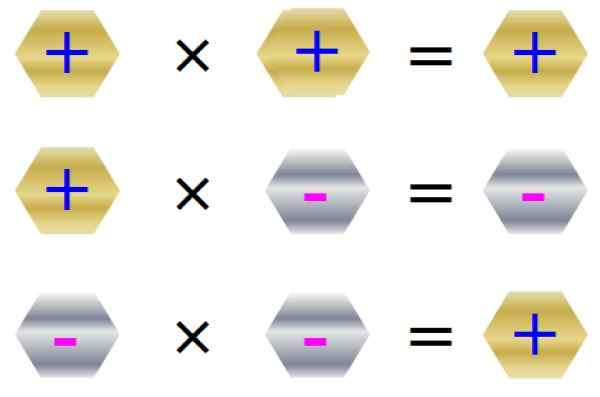Obrázok 3. Pravidlo znamenia pre násobenie. Zdroj: f. Zapata.

Násobenie

-Kombutivita: Poradie faktorov nemení produkt, preto ≠ = b.Kde sú A a B negatívne, celé alebo frakčné čísla.

Môže vám slúžiť: Iracionálne čísla: História, vlastnosti, klasifikácia, príklady

-Asociativita: Nech je to splnené celé čísla a, b a c.b). C = a. (B.c)

-Distribúcia týkajúca sa sumy: Nechajte celé čísla A, B a C, platí. (b+c) = a.B +a.c

Príklad

(-3/2) x [(-5) + (+4)-( + 2)] = (-3/2) x (-5) + (-3/2) x (+4) + (- 3/2) x (-2) = (15 - 12 + 6)/2 = 9/2

Operácia medzi štvorcovými zátvorkami mohla byť tiež vyriešená a výsledok vynásobený (-3/2), ako je tento:

(-3/2) x [-5 + 4-2] = (-3/2) x (-3) = 9/2

Rozdelenie

Pravidlo znakov pre rozdelenie je vystavené na tomto obrázku:

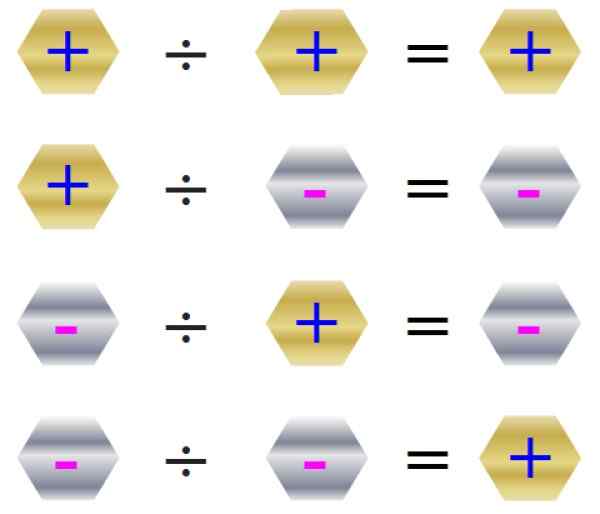Obrázok 4. Podpisy pravidla pre rozdelenie. Zdroj: f. Zapata.

Divízia nie je komutatívna a zvyčajne na ÷ b ≠ B ÷ a, nie je povolené rozdelenie medzi 0. Pozrime sa na príklad:

(-54) ÷ (+3) = -18

Na získanie tohto výsledku je kvocient jednoducho hotový a značka sa vyberie podľa tabuľky uvedenej na obrázku, ktorá zodpovedá tretej možnosti hore dole.

Zosilnenie

Potenciácia je prevádzka formulára doⁿ, Kde je základňa a n je exponent. Základňa a exponent môžu mať akékoľvek znamenie.

-Ak je základňa negatívna alebo pozitívna a exponent je celý, výsledok operácie je vždy pozitívny.

-Keď je základňa pozitívna a exponent je úplne výsledkom je pozitívny.

-A ak je základňa záporná a exponent je nepárny, výsledok je negatívny.

Frakčné exponenty sa budú striedavo vyjadriť ako koreň, napríklad odmocninový koreň ekvivalentný s frakčným exponentom ½, kubický koreň sa rovná exponentu 1/3 atď.

Pozrime sa na niekoľko príkladov:

a) (-3)³ = (-3) x (-3) x (-3) = -27

b) 16 ^-1/2 = 1 / √16 = ¼

c) (+8) ^1/3 = kubický koreň 8 = 2

Odkazy

1. Baldor, a. 1986. Aritmetika. Vydania a distribúcie Codex.
2. Figuera, J. 2000. Matematika 7. Stupeň. Edície Co-Bo.
3. Jiménez, r. 2008. Algebra. Sála.
4. Matematika je zábava. Ako pridať a odpočítať pozitívne a záporné čísla. Získané z: Mathisfun.com
5. Wikipedia. Záporné čísla. Obnovené z: je.Wikipedia.orgán.