Vlastnosti imaginárnych čísel, aplikácie, príklady

Ten Imaginárne čísla Sú to tie, ktoré dávajú riešenie rovnici, v ktorej sa neznámy, štvorcový zvýšený, rovná skutočnému zápornému číslu. Imaginárna jednotka je I = √ (-1).

V rovnici: z²= - a, z Je to imaginárne číslo, ktoré je vyjadrené takto:

 Z = √ (-a) = i√ (a)

Bytosť do Pozitívne skutočné číslo. Jo A = 1, tak z = i, kde Jo je imaginárna jednotka.

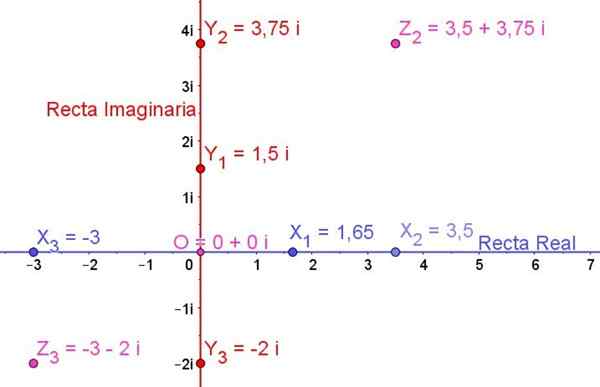postava 1. Komplexná rovina ukazujúca niektoré reálne čísla, niektoré imaginárne čísla a niektoré zložité čísla. Zdroj: f. Zapata.

Všeobecne platí, že imaginárne číslo Z je vždy vyjadrené vo forme: 

z = y⋅i

Kde a Je to skutočné číslo a Jo je imaginárna jednotka.

Ako aj skutočné čísla sú zastúpené na riadku, nazývané Skutočný, Analogické imaginárne čísla sú zastúpené na Imaginárny rovný.

Ten Imaginárny rovný Je to vždy ortogonálne (90 ° formu) k Skutočný a tieto dve čiary definujú karteziánsku rovinu zvanú Komplexná rovina.

Obrázok 1 zobrazuje komplexnú rovinu a niektoré reálne čísla, na nej sú znázornené niektoré imaginárne čísla a tiež niektoré zložité čísla:

X₁, X₂, X₃ Sú to skutočné čísla

A₁, A₂, A₃ Sú to imaginárne čísla

Z₂ a z₃ Sú to zložité čísla

Číslo alebo je skutočné nula a je tiež imaginárnou nulou, takže pôvod alebo je nulový komplex vyjadrený pomocou:

0 + 0i 

[TOC]

Vlastnosti

Sada imaginárnych čísel je označená::

I = …, -3i,…, -2i,… .,-Jo, .. .,0i, .. .,Jo, .. .,2i, .. .,3i, ...

A je možné definovať niektoré operácie týkajúce sa tejto číselnej sady. Imaginárne číslo sa z týchto operácií vždy získa, takže ich uvidíme s trochu podrobnejšími:

Súčet a odčítanie imaginárnych

Imaginárne čísla sa môžu navzájom pridávať a odpočítať, a preto bude existovať nové imaginárne číslo. Napríklad:

Môže vám slúžiť: relatívnych bratrancov: Čo sú, vysvetlenie, príklady

 3i + 2i = 5i

4i - 7i = -3i

Imaginárny produkt

Ak sa uskutoční produkt imaginárneho čísla s iným, výsledkom je skutočné číslo. Urobme nasledujúcu operáciu, aby sme skontrolovali:

2i x 3i = 6 x i² = 6 x (√ (-1))² = 6 x (-1) = -6.

A ako vidíme, -6 je skutočné číslo, hoci sa získalo vynásobením dvoch čistých imaginárnych čísel.

Produkt skutočného čísla pre ďalšie imaginárne

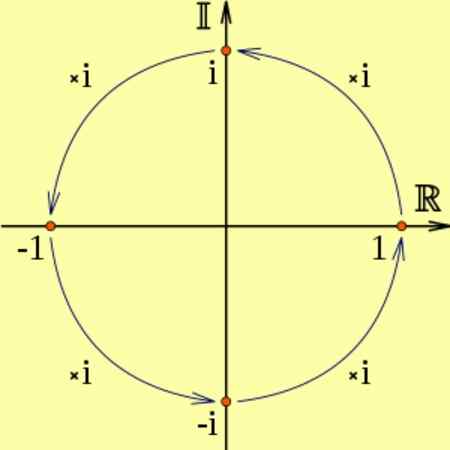
Ak sa skutočné číslo vynásobí I, výsledkom bude imaginárne číslo, ktoré zodpovedá rotácii 90 stupňov.

A je to ja² zodpovedá dvom po sebe idúcim rotáciám 90 stupňov, čo je ekvivalentné vynásobeniu -1, to znamená ja² = -1. Je to vidieť v nasledujúcom diagrame:

Obrázok 2. Násobenie imaginárnou jednotkou a zodpovedá 90 ° rotáciám. Zdroj: Wikimedia Commons.

Napríklad:

-3 x 5i = -15i

-3 x i = -3i.

Potenciácia imaginárneho

Je možné definovať zosilnenie imaginárneho čísla na celý exponent:

Jo¹ = i

Jo² = i x i = √ (-1) x √ (-1) = -1

Jo³ = i x i² = -I

Jo⁴ = i² x i² = -1 x -1 = 1

Jo⁵ = i x i⁴ = i

Vo všeobecnosti musíte Joⁿ = i^(n mod 4), kde Mód Je to zvyšok rozdelenia medzi n a 4.

Môže sa tiež vytvoriť potenciácia negatívnych celých čísel:

Jo^-1 = 1 / i¹ = i / (i x i¹) = I / (i²) = I / (-1) = -i

Jo-² = 1 / i² = 1/ (-1) = -1

Jo-³= 1 / i³ = 1 / (-i) = (-1) / i = -1 x i^-1 = (-1) x (-i) = i

Všeobecne platí, že imaginárne číslo B kedy bude vyvýšené na výkon n:

(B⋅i) iⁿ = bⁿ Joⁿ = bⁿ i^(n mod 4)

Niektoré príklady sú nasledujúce:

(5 i)¹² = 5¹² Jo¹² = 5¹² Jo⁰ = 5¹² x 1 = 244140625

(5 i)^jedenásť = 5^jedenásť Jo^jedenásť = 5^jedenásť Jo³ = 5^jedenásť x (-i) = -48828125 i

(-2 i)¹⁰ = -2¹⁰ Jo¹⁰ = 2¹⁰ Jo² = 1024 x (-1) = -1024

Súčet skutočného čísla a jedného imaginárneho

Ak sa pridá skutočné číslo s imaginárnym, výsledok nie je ani skutočný, ani imaginárny, je to nový typ čísla nazývaný Zložité číslo.

Napríklad, ak x = 3,5 a y = 3,75i, výsledkom je komplexné číslo:

Môže vám slúžiť: minimálne štvorce

Z = x + y = 3,5 + 3,75 i

Všimnite si, že skutočné a imaginárne časti nemôžu byť zoskupené do sumy, takže zložité číslo bude mať vždy skutočnú časť a ďalšiu imaginárnu časť.

Táto operácia rozširuje súbor reálnych čísel na najširšie zložité čísla.

Žiadosti

Názov imaginárnych čísel navrhol francúzsky matematik René Descartes (1596-1650) ako výsmech alebo nesúhlas s ich návrhom, ktorý predložil taliansky matematik Raffaelle Century Bombelli.

Ďalší veľkí matematici, ako napríklad Euler a Leibniz, vyslali Descartes v tejto nezhode a nazývali imaginárne čísla ako obojživeď, o ktorých sa diskutovalo medzi bytosťou a ničím.

Meno imaginárnych čísel sa dodáva dnes, ale jeho existencia a dôležitosť je veľmi skutočná a hmatateľná, pretože sa objavujú prirodzene v mnohých odboroch fyziky, napríklad:

-Teória relativity.

-V elektromagnetizme.

-Kvantová mechanika.

Cvičte s imaginárnymi číslami

- Cvičenie 1

Nájdite riešenia nasledujúcej rovnice:

z² + 16 = 0

Riešenie

z² = -16

Užívanie druhého koreňa v oboch členoch, ktorých máte:

√ (z² ) = √ (-16)

± z = √ (-1 x 16) = √ (-1) √ (16) = i x 4 = 4i

Inými slovami, riešenia pôvodnej rovnice sú:

z = +4i alebo z = -4i.

- Cvičenie 2

Nájdite výsledok zvýšenia imaginárnej jednotky na napájanie 5 mínus odpočítanie Imaginárna jednotka zvýšená na výkon -5.

Riešenie

Jo⁵ - Jo-⁵ = i⁵ - 1/i⁵ = i - 1/i = i - (i)/(i x i) = i - i/( - 1) = i + i = 2i

- Cvičenie 3

Nájdite výsledok nasledujúcej operácie:

(3i)³ + 9i 

Riešenie

3³ Jo³ - 9 = 9 (-i) + 9i = -9i + 9i = 0i

- Cvičenie 4

Nájdite riešenia nasledujúcej kvadratickej rovnice:

Môže vám slúžiť: Existencia a jedinečnosť veta: demonštrácia, príklady a cvičenia

(-2x)² + 2 = 0

Riešenie

Rovnica je usporiadaná takto:

(-2x)² = -2

Potom si vezmite druhý koreň v oboch členoch

√ ((-2x)²) = √ (-2)

± (-2x) = √ (-1 x 2) = √ (-1) √ (2) = i √ (2) = √2 i

Potom sa konečne získa x:

x = ± √2 / 2 i

To znamená, že existujú dve možné riešenia:

x = (√2 / 2) i

Alebo toto ďalšie:

x = - (√2 / 2) i

- Cvičenie 5

Nájdite hodnotu z definovanú:

Z = √ (-9) √ (-4) + 7

Riešenie

Vieme, že druhý druhý koreň záporného skutočného čísla je imaginárne číslo, napríklad √ (-9) sa rovná √ (9) x √ (-1) = 3i.

Na druhej strane, √ (-4) sa rovná √ (4) x √ (-1) = 2i.

Takže pôvodnú rovnicu je možné nahradiť:

3i x 2i - 7 = 6 i² - 7 = 6 (-1) -7 = -6 -7 = -13

- Cvičenie 6

Nájdite hodnotu Z v dôsledku nasledujúceho rozdelenia dvoch zložitých čísel:

Z = (9 - i²) / (3 + i)

Riešenie

Čitateľ výrazu môže faktorovať pomocou nasledujúcej vlastnosti:

Rozdiel štvorcov je produktom súčtu rozdielom binomiálov bez zvýšenia štvorca.

Tak:

Z = [(3 - i) (3 + i)] / (3 + i)

Výsledný výraz sa potom zjednoduší zostávajúcim

Z = (3 - i)

Odkazy

1. Gróf, r. Zložité čísla. Získané z: matematiky.vôl.Ac.Uk.
2. Figuera, J. 2000. Matematika 1. Diverzifikovaný. Edície Co-Bo.
3. Hoffmann, J. 2005. Výber matematických problémov. Publikácie Monfort.
4. Jiménez, r. 2008. Algebra. Sála.
5. Wikipedia. Imaginárne číslo. Zdroj: In.Wikipedia.orgán