Definícia a charakteristiky nulového uhla, príklady, cvičenia

On uhol Je to ten, ktorého opatrenie má hodnotu 0, a to v stupňoch aj v Radiane alebo inom systéme merania uhlov. Preto mu chýba amplitúda alebo otváranie, napríklad medzi dvoma paralelnými čiarami.

Aj keď jeho definícia znie celkom jednoducho, nulová uhol je veľmi užitočný v mnohých fyzických a inžinierskych aplikáciách, ako aj v navigácii a dizajne.

postava 1. Medzi rýchlosťou a zrýchlením vozidla je nulová uhol, preto auto ide rýchlejšie a rýchlejšie. Zdroj: Wikimedia Commons.

Existujú fyzikálne množstvá, ktoré musia byť zarovnané paralelne, aby sa dosiahli určité účinky: ak sa auto pohybuje priamo na diaľnici a medzi jeho rýchlostným vektorom vložka a jeho vektorové zrýchlenie do Je 0 °, auto sa zvyšuje.

Na nasledujúcom obrázku sa objavujú rôzne typy uhla vrátane nulového uhla napravo. Ako je vidieť, uhol 0 chýba amplitúda alebo otvorenie.

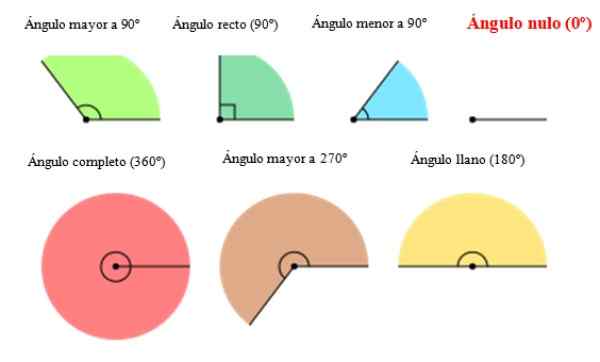Obrázok 2. Typy uhlov, vrátane nulového uhla. Zdroj: Wikimedia Commons. Orias [CC BY-SA (https: // creativeCommons.Org/licencie/By-SA/3.0)].[TOC]

Príklady nulových uhlov

Je známe, že rovnobežné čiary tvoria uhol null. Ak máte horizontálnu čiaru, je to rovnobežné s x -osou karteziánskeho súradnice, a preto je jeho sklonom v porovnaní s ním 0. Inými slovami, vodorovné čiary majú nulový sklon.

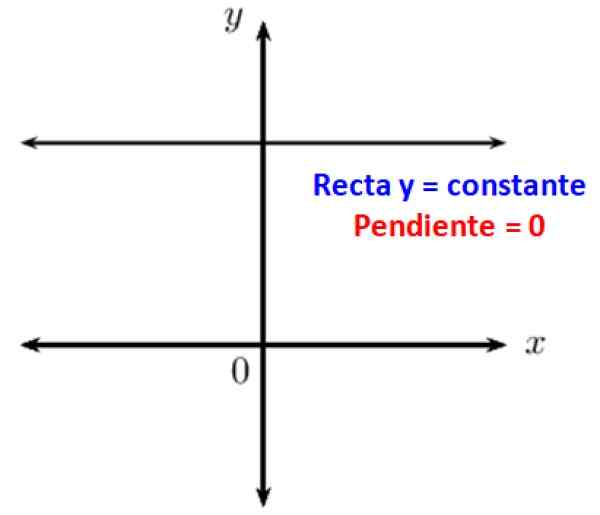Obrázok 3. Vodorovné čiary majú nulovú čakajúcu. Zdroj: f. Zapata.

Aj trigonometrické dôvody nulového uhla sú 0, 1 alebo nekonečno. Preto je NULL uhol prítomný v mnohých fyzických situáciách, ktoré zahŕňajú operácie s vektormi. Tieto dôvody sú:

Môže vám slúžiť: usporiadaný pár

-Sen 0 ° = 0

-cos 0 ° = 1

-Tg 0 ° = 0

-Sec 0 ° = 1

-Poškodenie 0 ° → ∞

-CTG 0 ° → ∞

A budú užitočné na analýzu niektorých príkladov situácií, v ktorých prítomnosť nulového uhla zohráva základnú úlohu:

- Účinky nulového uhla na fyzikálne veľkosti

Súčet vektorov

Keď sú dva vektory rovnobežné, uhol medzi nimi je nula, ako je vidieť na obrázku 4 vyššie. V tomto prípade sa súčet oboch vykonáva umiestnením jedného po druhom a veľkosťou vektora je súčet veľkosti dodatkov (obrázok 4b).

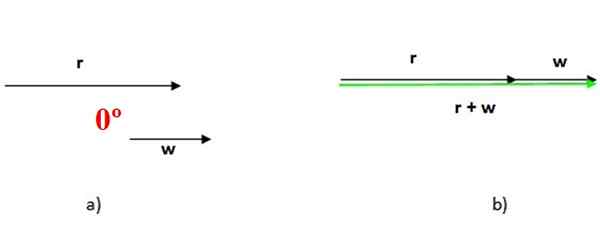Obrázok 4. Súčet paralelných vektorov, v tomto prípade je uhol medzi nimi nulové uhol. Zdroj: f. Zapata.

Keď sú dva vektory rovnobežné, uhol medzi nimi je nula, ako je vidieť na obrázku 4 vyššie. V tomto prípade sa súčet oboch vykonáva umiestnením jedného po druhom a veľkosťou vektora je súčet veľkosti dodatkov (obrázok 4b)

Krútiaci moment alebo krútiaci moment

Krútiaci moment alebo krútiaci moment spôsobuje rotáciu tela. Závisí to od rozsahu aplikovanej sily a toho, ako sa uplatňuje. Veľmi reprezentatívnym príkladom je anglický kľúč obrázka.

Na dosiahnutie najlepšieho efektu otočenia sa sila kolmá na kľúčovú rukoväť, buď hore alebo dole, ale otáčanie sa neočakáva, ak je sila rovnobežná s rukoväťou.

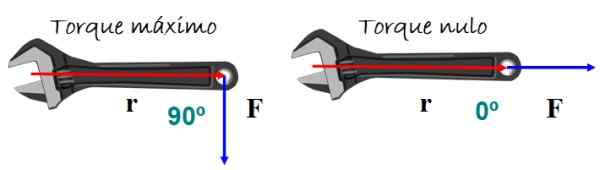Obrázok 5. Ak je uhol medzi polohou a pevnými vektormi prázdny, k krútiacemu momentu sa nevyskytuje, a preto neexistuje žiadny efekt otočenia. Zdroj: f. Zapata.

Matematicky krútiaci moment τ Je definovaný ako vektor alebo krížový produkt medzi vektormi r (polohový vektor) a F (Vektor sily) na obrázku 5:

Môže vám slúžiť: Štatistické vetvy

τ = r X F

Rozsah krútiaceho momentu je:

τ = r f sen θ

Byť 9 uhol medzi r a F. Keď je sin 9 = 0 moment je neplatný, v takom prípade 9 = 0 ° (alebo tiež 180 °).

Prietok elektrického poľa

Prietok elektrického poľa je skalárna veľkosť, ktorá závisí od intenzity elektrického poľa, ako aj od povrchovej orientácie, cez ktorú prechádza.

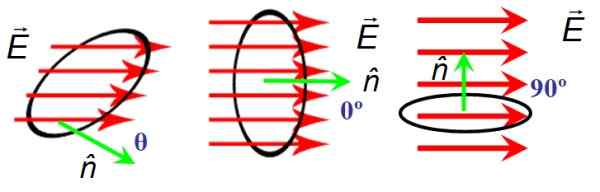
Na obrázku 6 je kruhový povrch plochy a cez ktorý prechádzajú elektrické polia A. Povrchová orientácia je daná normálnym vektorom n. Vľavo pole a normálny vektor tvoria ľubovoľný uhol 9, v strede tvoria nulové uhol a pravá sú kolmo.

Kedy A a n Sú kolmé, línie poľa neprechádzajú povrchom, a preto je tok nula, zatiaľ čo uhol medzi uhlom medzi A a n Je prázdno, čiary úplne prechádzajú povrchom.

Označovanie toku elektrického poľa gréckym písmenom φ (znie „fi“), jeho definícia jednotného poľa ako na obrázku, zostáva takto:

Φ = A•nDo

Bod uprostred oboch vektorov označuje bod alebo skalárny produkt, ktorý striedavo definuje:

Φ = A•nA = eacosθ

Tučné a šípky nad písmenom sú zdroje na rozlíšenie vektora a jeho veľkosť, ktorý je označený normálnymi písmenami. Pretože cos 0 = 1, prietok je maximálny, keď A a n Sú rovnobežné.

Obrázok 6. Prietok elektrického poľa závisí od orientácie medzi povrchom a elektrickým poľom. Zdroj: f. Zapata.

Cvičenia

- Cvičenie 1

Dve sily P a Otázka Pôsobia súčasne na včasnom objekte X, obe sily spočiatku tvoria uhol 9 medzi nimi. Čo sa stane s veľkosťou výslednej sily, keď 9 klesá, kým sa nezruší?

Môže vám slúžiť: hodnotenie funkcií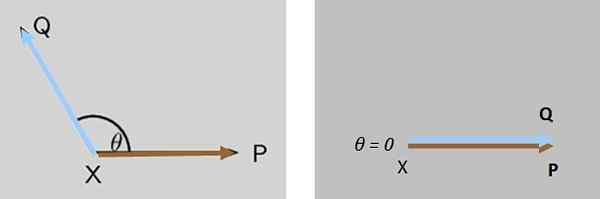 Obrázok 7. Uhol medzi dvoma silami pôsobiacimi na telo klesá, až kým veľkosť výslednej sily nezíska jej maximálnu hodnotu v tomto prípade. Zdroj: f. Zapata.

Riešenie

Veľkosť výslednej sily Otázka + P Postupne sa zvyšuje, až kým nie je maximálne Otázka a P Sú úplne rovnobežné (obrázok 7 vpravo).

- Cvičenie 2

Uveďte, či je uhol nuly riešením nasledujúcej trigonometrickej rovnice:

cos 2x = 1 + 4se x

Riešenie

Trigonometrická rovnica je taká, v ktorej je neznáma súčasťou argumentu trigonometrického dôvodu. Na vyriešenie navrhovanej rovnice je vhodné použiť vzorec pre kozine s dvojitým uhlom:

cos 2x = cos² X - sen² X

Pretože týmto spôsobom sa argument na ľavej strane stáva X namiesto 2x. Tak:

cos² X - sen² x = 1 + 4sen x

Na druhej strane cos² X + sen² x = 1, takže:

cos² X - sen² x = cos² X + sen² x + 4sen x

Termín cos² x je zrušený a zostáva:

- SEN² x = sen² x + 4sen x → - 2sen² x - 4senx = 0 → 2sen² x + 4senx = 0

Teraz sa uskutoční ďalšia zmena premennej: senx = u a rovnica sa zmení na:

2U² + 4U = 0

2U (u+4) = 0

Ktorých riešenia sú: u = 0 a u = -4. Vráťte zmenu, že by sme mali dve možnosti: sin x = 0 a senx = -4. Toto posledné roztok nie je životaschopné, pretože prsník akéhokoľvek uhla je medzi -1 a 1, takže nám zostane prvou alternatívou:

hriech x = 0

Preto x = 0 ° je roztok, ale tiež slúži na akýkoľvek uhol, ktorého sínus je 0, ktorý môže byť tiež 180 ° (π radiany), 360 ° (2 π radiány) a tiež príslušné negatívy.

Najbežnejším riešením trigonometrickej rovnice je: x = kπ, kde k = 0, ± 1, ± 2, ± 3, .. . k Celé číslo.

Odkazy

1. Baldor, a. 2004. Geometria plochej a vesmíru s trigonometriou. Kultúrne publikácie s.Do. c.Vložka. Mexiko.
2. Figueroa, D. (2005). Séria: Fyzika pre vedu a inžinierstvo. Zväzok 3. Častice. Editoval Douglas Figueroa (USB).
3. Figueroa, D. (2005). Séria: Fyzika pre vedu a inžinierstvo. Zväzok 5. Elektrická interakcia. Editoval Douglas Figueroa (USB).
4. Onlinemathlearning. Typy uhlov. Zdroj: OnlineMathlearning.com.
5. Zill, D. 2012. Algebra, trigonometria a analytická geometria. McGraw Hill Inter -American.