Násobenie zlomkov, ako sa to robí, príklady, cvičenia

Ten Násobenie zlomkov Je to aritmetická operácia medzi dvoma alebo viacerými frakciami, ktorá vedie k novému zlomku. Jeho čitateľ vynásobí čitateľov zúčastnených frakcií a menovateľ je rovnakým spôsobom.

Pozrime sa na to s príkladom na nasledujúcom obrázku. Predpokladajme, že existujú dva frakcie A/B a C/D, s B a D sa líšia od 0.

postava 1. Násobenie frakcií je operácia, ktorá sa vykonáva online. Zdroj: f. Zapata.

Vykonanie násobenia medzi nimi je produkt vyrobený medzi čitateľmi a tiež menovateľom menovateľov. Týmto spôsobom sa vytvorí nová frakcia tam, kde sú čitateľ a menovateľ: (A × C) a (B × D).

Tento postup sa ľahko rozšíri na znásobenie troch a ďalších zlomkov. Pozrime sa nižšie.

Ako sa vykonáva násobenie frakcií?

Produkt môže byť symbolizovaný krížom alebo bodom rozptýleným medzi zlomkami. Okrem toho je potrebné vziať do úvahy, že frakcie môžu mať kladné znamenie alebo negatívne znamenie, takže je potrebné dávať pozor, aby ste sa riadili pravidlom znakov:

-Keď sa vynásobia dve čísla rovnakého znaku, produkt je pozitívny.

-Ak sa vynásobia dve sumy rôznych príznakov, výsledok je záporný.

Tadiaľto:

Po vykonaní postupu je frakcia zjednodušený, ak je to možné. To v prípade, že čitateľ a menovateľ nie sú navzájom bratrancami. Napríklad:

Ak čitateľ a menovateľ zúčastnených frakcií nie sú navzájom bratrancami, je vhodné ich zjednodušiť pred vykonaním násobenia frakcií. Týmto spôsobom sa pri spustení výrobkov získajú menšie a zvládnuteľnejšie čísla.

Môže vám slúžiť: Koľko riešení má kvadratickú rovnicu?

Vlastnosti násobenia frakcií

Produkt od 0

Akákoľvek frakcia vynásobená 0 ​​sa rovná 0:

Produkt 1

Akákoľvek frakcia vynásobená 1 sa rovná sebe samému:

Preto sa uvažuje 1 neutrálny prvok násobenie. Všimnite si, že celé číslo 1 má frakčný výraz:

Takým spôsobom, že sa dokážeme vynásobiť 1 akýmkoľvek zlomkom, pomocou pravidla už vysvetlené. Tak:

Komutatívne vlastníctvo

Násobenie frakcií je komutatívne, čo znamená, že poradie faktorov nemení produkt:

Asociatívna vlastnosť

Násobenie frakcií je tiež asociatívne, môžeme overiť vynásobením troch frakcií:

Kde, ako vždy, menovatelia b, d a f sa líšia od 0.

Slovami: Ak sa chystáme vynásobiť tri frakcie, môžeme sa rozhodnúť urobiť produkt prvých dvoch a vynásobíme výsledok tretím frakciou. Alebo vynásobte posledné dve a ich výsledok ho nakoniec vynásobí prvým z zlomkov.

Bez ohľadu na zvolené poradie, výsledok bude rovnaký. Skontrolujme to:

Na vykonanie operácie boli prvé dve frakcie vynásobené zľava doprava. Výsledok bol vynásobený treťou frakciou, aby sa dosiahol konečný výsledok.

Druhou alternatívou je vynásobiť posledné dve frakcie a zanechať prvé čakanie. Čitateľ môže vidieť, že stredný výsledok pozostáva z dvoch rôznych frakcií od tých, ktoré sa získali iným spôsobom. Ale konečný výsledok je rovnaký:

Distribučný majetok týkajúci sa sumy

Nechajte tri frakcie A/B, C/D a E/F, s B, D a F sa líšia od 0. Násobenie je distribučné vzhľadom na sumu.

Predpokladajme, že chceme vykonať nasledujúcu operáciu:

Spôsob, ako ju vykonať, prostredníctvom tejto nehnuteľnosti, je nasledujúci:

Môže vám slúžiť: Tukey Test: Čo je v prípade príkladu vyriešené cvičenie

Preto je produkt čísla pre súčet dvoch ďalších, môže sa vykonať pridaním dvoch produktov: prvý pre druhý a prvý po treťom. Príklad je veľmi jednoduchý:

Konečný výsledok sa javí zjednodušený na maximum, ako je vysvetlené vyššie.

Príklady

Násobenie frakcie celočíslom

Predpokladajme, že chcete znásobiť frakciu A/B celé číslo n:

Predtým sme videli, že číslo 1 sa dá vyjadriť ako frakcia, jednoducho umiestnenie ako menovateľ na 1. Môžeme to isté urobiť s akýmkoľvek celočíslom n, pretože jeho delenie 1 to vôbec nezmení. Tak:

Napríklad:

Príklad 2: Násobenie frakcie zmiešaným číslom

Zmiešané číslo alebo zmiešaná frakcia je taká, ktorá má celú časť a zlomkovú časť. Na vykonanie produktu takéhoto čísla, buď s zlomkom, iným zmiešaným číslom, alebo s celkovým číslom, je potrebné ho zmeniť na zlomok.

Frakcia, ktorá predstavuje zmiešané číslo, je a Nesprávny zlomok, A ktorého čitateľ má väčšiu absolútnu hodnotu ako menovateľ.

Môžeme to získať prostredníctvom súčtu celej časti, pohodlne vyjadrené ako frakcia umiestnením 1 ako menovateľa plus frakčnú časť.

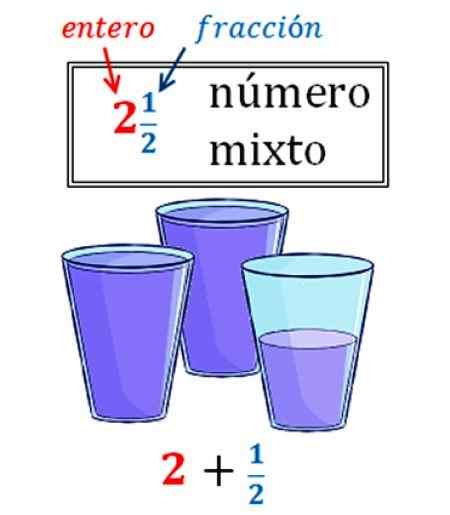Obrázok 2. Zmiešané číslo transformované na zlomok. Zdroj: Wikimedia Commons.

Na obrázku je príklad zmiešaného čísla, ktorý ukazuje, ako často. Máme 2 a pol pohárov vody, ktoré ako zmiešané číslo vyjadrujú takto:

2 ½

Dostávame nesprávny zlomok, ktorý ju predstavuje:

Teraz predpokladajme, že chceme nájsť 3/4 častí dvoch a pol pohárov vody. To, čo musíme urobiť, je vynásobenie 3/4 získanou nesprávnou frakciou:

Môže vám slúžiť: Poisson Distribúcia: vzorce, rovnice, model, vlastnosti

Vyriešené cvičenia

Cvičenie 1

Vykonajte nasledujúcu operáciu:

Riešenie

Číslo 1 ¾ je zmiešané číslo. Celá jeho časť je 1 a jej zlomková časť je ¾. Ak vykonáme operáciu: 1 + ¾, zmiešané číslo sa transformuje na nesprávnu frakciu.

1 + ¾ = (4 + 3) /4 = 7/4

Po transformácii zmiešaného čísla z nesprávnej frakcie sa násobenie vykonáva ako obvykle:

Cvičenie 2

Vek José je ½ z 2/3 veku Manuela. Ak má Manuel 24 rokov, aký je vek José?

Riešenie

Nech x vek José, neznámy, že musíme nájsť. Vo vyhlásení nám hovorí, že vek Manuela je 24 rokov, preto je táto hodnota známa.

Aby sme určili vek José, vykonávame operácie uvedené vyhlásením: „Vek José je ½ z 2/3 veku Manuela“.

Toto je násobenie dvoch frakcií pre celé číslo:

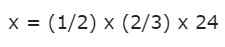
Prvé dve frakcie môžeme vynásobiť podľa pravidiel opísaných predtým. Číslo 24 je celé číslo, ale už vieme, že nie je problém s jeho transformáciou na zlomok, jednoducho umiestnením 1 ako menovateľa:

Môžeme značne zjednodušiť operáciu a poznamenať, že 2 v čitateľovi druhého frakcie je okamžite zrušený s 2, ktorý je menovateľom v prvom.

To je to, čo sme po zrušení zostali:

Preto má José 8 rokov.

Odkazy

1. Baldor, a. 1986. Aritmetika. Vydania a distribúcie Codex.
2. Carena, m. 2019. Matematická príručka. Národná univerzita pobrežia.
3. Jiménez, r. 2008. Algebra. Sála.
4. Matematika. Násobenie zlomkov. Získané z: Sangakoo.com.
5. Šikovný. Násobenie zlomkov. Získané z: Smartick.je.