Dvojitý odber vzoriek

Vysvetľujeme, čo je dvojitý odber vzoriek, príklady, výhody a nevýhody a vyriešené cvičenia

Pri dvojitom odbere vzoriek chcete hlbšie poznať premennú populácie

Čo je dvojitý odber vzoriek?

On Dvojitý odber vzoriek Je to technika, ktorá sa používa v inferenciálnych štatistikách, keď sa chcete dozvedieť viac detailov a istoty o konkrétnej premennej, ktorá charakterizuje určitú populáciu.

Vzorka druhej populácie sa všeobecne vykonáva po prvej vzorke, ktorej analýza nepreukázala a analyzovala sa štatisticky významný záver o žiadnej z premenných štúdie.

Z tohto dôvodu je odber vzoriek dvojitých štatistík známy aj ako Odber vzoriek dvoch fáz. Užitočnosť druhej vzorky leží, v ktorej pomáha presnejšie určiť odhady a regresie určitej pomocnej premennej, ktorá vzniká na základe analýzy prvej vzorky.

Ďalším použitím, ktoré sa poskytuje dvojitým odberom vzoriek, je zhromažďovanie informácií na realizáciu vzorkovania vrstvy.

Príklady

Nižšie sú rôzne situácie, v ktorých je dvojitý odber vzoriek opodstatnený.

Kontrola kvality pri vypracovaní kusov

Metóda dvojitého vzorkovania sa často používa pri kontrole priemyselnej kvality a zvyčajne sa vykonáva v dvoch fázach.

Predpokladajme napríklad priemyselný stroj, ktorý pripravuje určité kusy. Pokiaľ je stroj nastavený, žiadny kus nie je identický s iným, pretože v jeho rozmeroch a hmotnosti sa môžu vyskytnúť malé variácie. Ide o určenie, či veľa častí vyrobených pomocou uvedeného stroja spĺňa kritériá tolerancie tak, aby bola prijatá alebo zamietnutá.

Po prvé, odoberie sa náhodná vzorka kusov, s ktorou sa má skontrolovať jedna z premenných, napríklad dĺžka kusu, je vo vnútri tolerancie.

V prípade, že priemerná dĺžka je pod alebo nad požadovaným stupňom tolerancie pre uvedenú premennú, v tejto prvej vzorke sa potom odvodzuje, že šarža je chybná a musí sa zlikvidovať. V takom prípade nie je potrebné odobrať nové vzorky.

Môže vám slúžiť: korelačný koeficient: vzorce, výpočet, interpretácia, príklad

Naopak, ak je priemerná hodnota v rozsahu tolerancie, ale štandardná odchýlka vzorky je dostatočne veľká na súčet alebo odčítanie priemernej hodnoty je mimo okraja, potom bude potrebné zhromaždiť druhú hlavnú vzorku.

Táto druhá vzorka musí obsahovať pôvodnú vzorku, aby sa výpočty opakovali, a preto je schopná urobiť konečné rozhodnutie týkajúce sa skúmanej premennej. Týmto spôsobom je možné vedieť, či je časť chybná alebo nie.

Zníženie nákladov na odber vzoriek

Pri mnohých príležitostiach je ťažké získať prístup k jednej z premenných, ktoré chcete študovať. Ale môže existovať pomocná premenná pre zber údajov.

V tomto prípade sa odoberia dve vzorky, veľká pre pomocnú premennú, lacnejšiu a menšiu vzorku obsiahnutú v hlavnej vzorke najdrahšej premennej.

Táto metóda je použiteľná vždy, keď sa zistí, že existuje korelácia medzi oboma premennými, čo je vo všeobecnosti vzťahom proporcionality.

Príklad tejto situácie sa objavuje v lesných vedách, kde je potrebné určiť percento stromov postihnutých rastlinou parazita (la tiña).

Keďže sú veľmi rozsiahle a ťažko prístupné regióny, kompletná populácia stromov je v čase a nákladoch nemožná. Tieto kroky sa potom dodržiavajú:

Krok 1: odber vzoriek

Predbežný odber vzoriek by pozostával z použitia leteckej fotografie a les je rozdelený na pozemky. Niekoľko pozemkov je vybraných náhodne a odhaduje sa analýzou obrazov zvolených pozemkov, koľko stromov je postihnutých kruhovým červou, pretože farba stromov je ovplyvnená parazitom.

Môže vám slúžiť: Euklidová veta

Krok 2: Field Work

Fotografická analýza však nemusí byť presná, preto si vyberieme, pokiaľ možno náhodne niekoľko prvých vzoriek, ktoré robia prácu v teréne.

Krok 3: Porovnanie

Potom je výsledok poľa porovnávaný s fotografickými pre odpočúvanie dvoch pozemkov. Toto porovnanie je možné vykonať napríklad, napríklad vytvorenie grafu, v ktorom je horizontálna os hodnota získaná pre každú časť pomocou fotografie a vo vertikálnej osi hodnota získaná LOT prostredníctvom práce v teréne.

Táto grafická metóda umožňuje vizuálne identifikovať, či existuje alebo nie.

Po hlavnej vzorke, tj fotografickej vzorke, sa odoberie priemerná hodnota infikovaných stromov a jej štandardná odchýlka. Ale ako sa stanovil koeficient proporcionality a jej chyba so vzorkami poľa, potom je možné napraviť výsledok hlavnej vzorky (fotografický).

Potom je možné tento výsledok extrapolovať na úplnú populáciu stromov.

Výhody a nevýhody dvojitého odberu vzoriek

V opísaných príkladoch je nákladová výhoda dôkazom.

Nevýhodou je, že v prípade dvojitého odberu vzoriek pre kontrolu kvality existuje riziko prejdenia dobrým množstvom výrobkov, ktoré sú mimo tolerancie.

Cvičenie

Chcete odhadnúť počet chorých stromov v lese so 162 hektármi. Pretože les je veľmi rozsiahly, je rozdelený na 100 pozemkov tej istej oblasti. 18 pozemkov sa vyberá náhodne a prostredníctvom fotografickej štúdie sa odhaduje, že na týchto 18 pozemkoch je 8 chorých stromov so štandardnou chybou asi 4,5 stromov.

Môže vám slúžiť: Aké sú časti zlomku? (Príklady)

Z týchto 18 pozemkov je 8 pozemkov vybraných náhodne. Pre týchto osem pozemkov má fotografická štúdia 10 chorých stromov s chybou viac alebo menej 5,3 stromov.

Na druhej strane, pre tých istých osem pozemkov, poľná štúdia hodí 12,4 chorých stromov s chybou viac ako 6,3 stromov.

Požaduje sa:

• a) Stanovte koeficient proporcionality medzi poľnou štúdiou lineárnou regresiou.
• b) Odhadnite počet chorých stromov prostredníctvom fotografickej metódy na sto pozemkoch.
• c) Aplikujte korekciu so získaným koeficientom proporcionality, aby ste odhadli skutočný počet chorých stromov v celom lese.

Riešenie

Graf počtu stromov na fotografický počet oproti počtu poľa pre osem pozemkov vybraných pre obe štúdie.

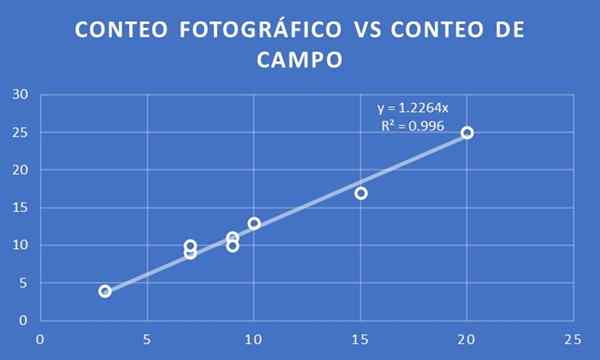Fotografický počet verzus počet v teréne. Zdroj: f. Zapata.

Trendová čiara je upravená a jeho sklon je určený. V tomto prípade sa získa, že koeficient proporcionality je 1,23. To znamená, že ak x je číslo fotografického počtu, potom sa odhaduje, že počet polí bude y = 1,23 x.

Počet chorých stromov podľa fotografického počtu v 18 vybraných pozemkoch bude:

18 x 8,5 = 153

Ale pretože celý les bol rozdelený na 100 pozemkov tej istej oblasti, počet chorých stromov odhadovaných fotografickou metódou je: (100/18) x 153 = 850.

Teraz sa používa korekčný faktor získaný z porovnania medzi poľnou a fotografickou štúdiou:

Odhadovaný skutočný počet chorých stromov v lese = 1,23 x 850 = 1046.

Odkazy

1. Dvojitá vzorka pre odhad pomeru, Pennstate College. Zdroj z PSU.Edu
2. Dvojité, viacnásobné a segenciálne vzorkovanie, NC Štátna univerzita. Zotavené z NCSU.Edu
3. Jednoduché náhodné odber vzoriek. Zotavené z Investopedie.com
4. Čo je dvojitý odber vzoriek? Získané z: NIST.Vláda
5. Vzorka. Zdroj: In.Wikipedia.orgán
6. Viacstupňová vzorka. Zdroj: In.Wikipedia.orgán