Príklady rovnobežníka, vyriešené cvičenia

On metóda rovnobežníka Je to grafická metóda na pridanie dvoch vektorov do roviny. Často sa používa na nájdenie výsledku dvoch síl aplikovaných na telo alebo dve rýchlosti, ako v prípade plavca, ktorý má v úmysle prekročiť rieku kolmo a je odklonený súčasným.

Na zostavenie rovnobežníka sa musí v bode zhodovať pôvod vektorov, ktoré sa majú pridať, nakreslené na stupnici.

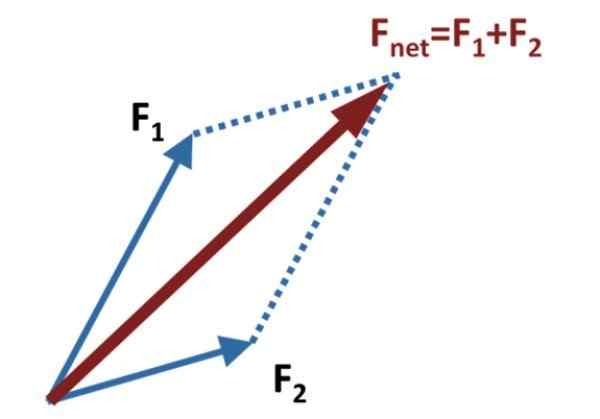
postava 1. Metóda rovnobežníka na pridanie dvoch vektorov. Zdroj: Wikimedia Commons.

Potom sa kreslia pomocné čiary rovnobežne s každým vektorom, ktorý dosahuje koniec druhého, ako je to znázornené na hornom obrázku.

Pridaný alebo výsledný vektor, tiež nazývaný sieťová sila, je vektor F_slepo, to sa získa nakreslením vektora, ktorý prechádza zo spoločného pôvodu F₁ a F₂, do bodu, kde sa pretínajú pomocné paralelné čiary. V diagrame obrázku sú znázornené bodkovanými čiarami.

Metóda prijíma svoj názov z obrázku, ktorý je tvorený závislými a pomocnými čiarami, čo je presne rovnobežník. Hlavným uhlopriečkou rovnobežníka je súčet vektor.

Je veľmi dôležité zdôrazniť, že poradie, v ktorom sú umiestnené ďalšie vektory.

[TOC]

Príklad metódy rovnobežníka krok za krokom

Nasledujúci obrázok zobrazuje vektory vložka a alebo V ľubovoľných jednotkách. Vektor vložka Opatrenia 3.61 jednotiek a tvorí uhol 56.3. s horizontálnym, zatiaľ čo alebo Opatrenia 6.32 jednotiek a uhol 18.4 ° týkajúce sa tejto referenčnej čiary.

Môže vám slúžiť: náhodná chyba: vzorec a rovnice, výpočet, príklady, cvičenia

Nájdeme váš vektor, ktorý pridáva metódu rovnobežníka.

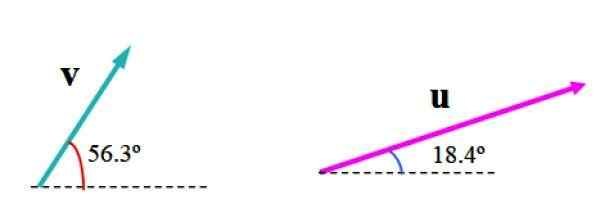Obrázok 2. Akékoľvek dva vektory v lietadle, z ktorých chceme nájsť výsledný vektor. Zdroj: f. Zapata

Je potrebné zvoliť vhodnú stupnicu, ako napríklad rozsah znázornený na nasledujúcom obrázku, v ktorom bola rovina vydelená mriežkou. Šírka štvorca predstavuje jednu (1) jednotku.

Keďže vektory sa nemenia, keď sa prenášajú, sú umiestnené takým spôsobom, že ich pôvod sa zhoduje s pôvodom súradníckeho systému (obraz vľavo).

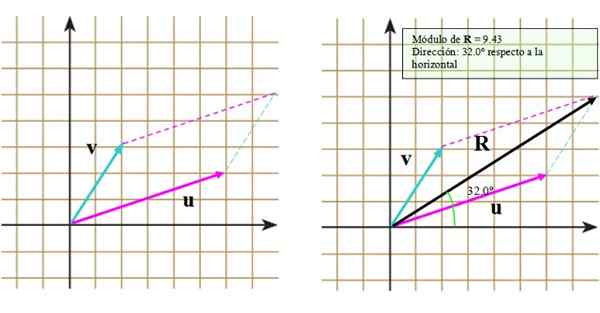Obrázok 3. Súčet vektorov prostredníctvom metódy rovnobežníka. Zdroj: f. Zapata.

Teraz sa poďme na tieto kroky:

1. Vektor koniec vektora vložka Segmentovaná čiara, ktorá je rovnobežná s vektorom alebo.
2. Opakujte postup, ale tentoraz s koncom vektora alebo.
3. Nakreslite hlavnú uhlopriečku, ktorá sa rozširuje od spoločného pôvodu do bodu priesečníka segmentovaných čiary.

Výsledok je možné vidieť na správnom obrázku, v ktorom sa objaví výsledný vektor R.

Ak chceme poznať rozsah R, Môžeme zmerať jeho dĺžku a porovnať ju s mierkou, ktorú máme. A pokiaľ ide o ich smer, vodorovná os alebo vertikálna os sa môže použiť napríklad ako referencie.

Použitím vodorovnej osi alebo osi x je uhol, ktorý R forma s touto osou sa meria pomocou dopravníka a týmto spôsobom poznáme adresu R.

Tiež veľkosť a smer R Môžu byť vypočítané vetami kosínutia a prsníka, pretože vytvorený rovnobežník sa dá rozdeliť do dvoch zhodných trojuholníkov, ktorých strany sú moduly vektorov alebo, vložka a R. Pozri príklad vyriešený 1.

Môže vám slúžiť: Okamžitá rýchlosť: definícia, vzorec, výpočet a cvičenia

Osobitný prípad: súčet kolmých vektorov

Keď sú vektory kolmé na seba, je formovaný obrázok, je obdĺžnik. Výsledný vektorový modul zodpovedá dĺžke diagonálu, ktorú je možné ľahko vypočítať pomocou vety Pythagory.

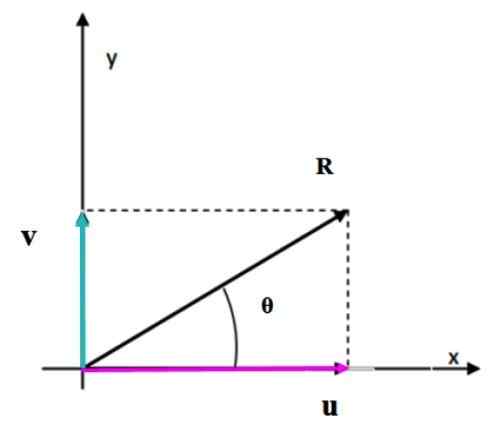Obrázok 4. Súčet dvoch kolmých vektorov pomocou metódy rovnobežníka. Zdroj: f. Zapata.

Vyriešené cvičenia

- Cvičenie 1

Máte vektor vložka, ktoré meria 3.61 jednotiek a tvorí uhol 56.3. s vodorovným a vektorom alebo, ktorého opatrenie je 6.32 jednotiek a tvorí uhol 18.4. (obrázok 2). Určite výsledný vektorový modul R = alebo + vložka a smer, ktorý tvorí uvedený vektor s vodorovnou osou.

Riešenie

Metóda rovnobežníka sa používa podľa vyššie uvedených krokov, aby sa získal vektor R. Ako už bolo uvedené, ak sú vektory starostlivo nakreslené po stupnici a používajú pravidlo a transportér, veľkosť a smer R Meria sa priamo na výkrese.

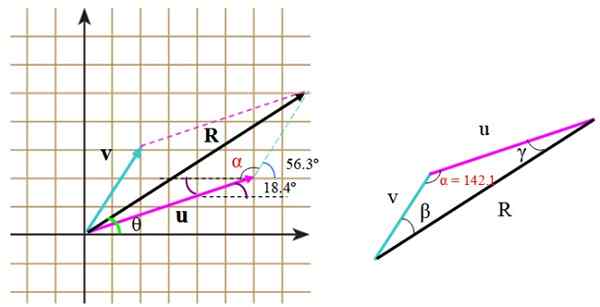Obrázok 5.- Výpočet veľkosti a smeru výsledného vektora. Zdroj: f. Zapata.

Môžu sa tiež vypočítať priamo pomocou trigonometrie a vlastností uhlov. Ak sa vytvorený trojuholník nie je obdĺžnik, ako v tomto prípade sa na nájdenie chýbajúcej strany aplikuje kosínová veta.

V pravom trojuholníku strany merajú u, v a r. Aby sa uplatňovala kosínová veta, je potrebné poznať uhol medzi vložka a alebo, ktoré nájdeme s pomocou mriežky, pričom správne umiestni uhly dodané vyhlásením.

Tento uhol je α a je zložený z:

a = (90-56.3.) + 90 ° +18.4. = 142.1

Môže vám slúžiť: červený trpaslík

Podľa Coseno Theorrem:

R² = v² + alebo² - 2U⋅v⋅cos α = 3.61² + 6.32² - 23.61 × 6.32 × cos 142.1. = 88.98

R = 9.43 jednotiek.

Nakoniec uhol medzi R A horizontálna os je 9 = 18.4 ° + γ. Uhol γ sa nachádza vetou prsníka:

sin α / r = sen γ / u

Preto:

sin y = v (sin a / r) = 3.61 x (sen 142.1. / 9.43)

γ = 13.6

9 = 18.4 ° + 13.6 ° = 32 °

- Cvičenie 2

Plavec sa pripravuje na prekročenie rieky, ktoré plávajú kolmo na prúd s konštantnou rýchlosťou 2.0 m/s. Plavec začína od A, ale končí v B, po prúde, kvôli prúdu, ktorý ho odklonil.

Ak je rýchlosť prúdu 0.8 m/s a všetky rýchlosti majú nájsť rýchlosť plavca, ako vidí pozorovateľ stojaci na brehu.

Riešenie

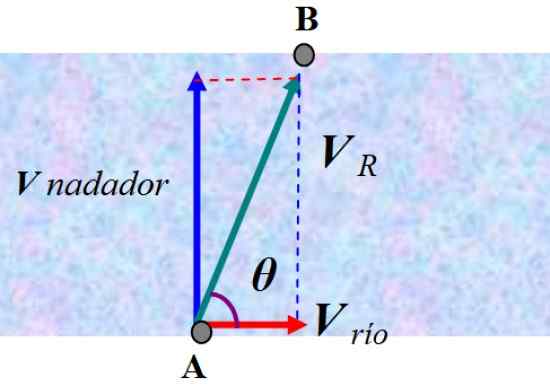Obrázok 6. Súčet rýchlostí metódou rovnobežníka. Zdroj: f. Zapata.

Pozorovateľ stojaci na brehu by videl, ako je plavec odklonený podľa výslednej rýchlosti Vložka_R. Aby sme našli odpoveď, musíme pridať rýchlosť plavca a rýchlosť prúdu, ktorú voláme Vložka _rieka:

Vložka _R = Vložka _plavec + Vložka _rieka

Na obrázku, ktorý nie je na stupnici, boli pridané vektory, aby sa získali Vložka _R. V tomto prípade je možné uplatniť vetu Pythagoras na získanie svojej veľkosti:

Vložka_R² = 2.0² + 0.8² = 4.64

Vložka_R = 2.15 m/s

Adresa, v ktorej sa ľahko vypočíta plavec kolmého smeru, ktorý si všimol:

9 = arctg (2/0.8) = 68.Druhý

Potom sa plavec líši 90 ° - 68.2. = 27.2. z vašej pôvodnej adresy.

Odkazy

1. Bauer, w. 2011. Fyzika pre inžinierstvo a vedy. Zväzok 1. MC Graw Hill.
2. Bedford, 2000. Do. Mechanika pre inžinierstvo: statické. Addison Wesley.
3. Figueroa, D. (2005). Séria: Fyzika pre vedu a inžinierstvo. Zväzok 1. Kinematika. Editoval Douglas Figueroa (USB).
4. Giambattista, a. 2010. Fyzika. Druhý. Edimatizovať. McGraw Hill.
5. Sears, Zemansky. 2016. Fyzika univerzity s modernou fyzikou. 14. Edimatizovať. Zväzok 1.