Súčet grafickej metódy vektorov, príklady, vyriešené cvičenia

Ten súčet vektorov Je to prídavná operácia medzi vektormi, ktorá vedie k inému vektorovi. Vektory sa vyznačujú tým, že majú veľkosť a tiež smer a význam. Preto nie je možné ich vo všeobecnosti pridať, ako by sa to stalo s skalárnymi množstvami, to znamená pridávanie čísel.

Vektor získaný zo súčtu niekoľkých vektorov sa nazýva výsledný vektor. V mechanike hovoríme o výsledná sila, čo je vektorový súčet všetkých síl na tele. Tento výsledok je rovnocenný s množinou alebo systémom síl.

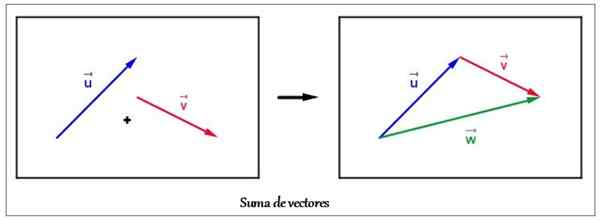
Na úplné zadanie vektora súčtu je potrebné označiť veľkosť a jednotu, smer a význam.

Je dôležité zdôrazniť, že pridaním vektorov musia predstavovať rovnakú fyzikálnu veľkosť, preto je vektorový súčet homogénnou operáciou. To znamená, že môžeme pridať jednu silu s inou, ale nie silou s presídlením, pretože výsledok nemá zmysel.

K dispozícii je niekoľko metód na nájdenie výsledného vektora: grafika a analytika. Ak chcete nájsť vektorové sumy s grafickými metódami, je založená na jednoduchej reprezentácii pre vektor, konkrétne segmentu orientovaného alebo šípky, ako je tento:

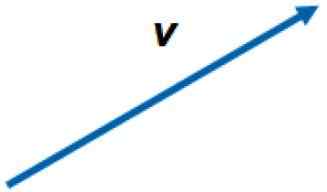Grafické znázornenie vektora v rovine. Zdroj: f. Zapata.

Vektory sú označené čiernymi písmenami v tlačenom texte alebo so šípkou cez písmeno, aby sa odlíšili od ich príslušných veľkostí alebo z skalárnych množstiev. Napríklad veľkosť vektora vložka Je to jednoducho vložka.

[TOC]

Grafická metóda na pridanie vektorov

Ak chcete pridať viac ako dva zvodové vektory, Polygónová metóda ani polygón, ktorý spočíva v prenose seba do každého z oslovených vektorov. Charakteristikou vektorov je to, že sú nemenné týkajúce sa prekladu, preto túto vlastnosť použijeme na stanovenie sumy.

Môže vám slúžiť: tepelná dilatácia

Začína sa s ktorýmkoľvek z vektorov, pretože prídavok vektora je komutatívny a poradie dodatkov nezmení sumu. Druhý vektor sa pohybuje dole a zodpovedá svojmu pôvodu s koncom prvého.

Potom sa dostane do ďalšieho vektora a potom vložte rovnaký postup, ktorý má zladiť pôvod s koncom predchádzajúceho. Postupujeme týmto spôsobom, aby sme umiestnili posledný vektor.

Výsledný vektor je ten, ktorý sa spája s pôvodom prvého s voľným koncom posledného. Názov tejto metódy vychádza z obrázku, ktorý výsledkom je: Polygon.

Príklad

Súčet príklad dvoch vektorov v rovine grafickou metódou. Zdroj: Wikimedia Commons

Zoberme si ako príklad sumu dvoch vektorov alebo a vložka to je znázornené na hornom obrázku.

Počnúc vektorom alebo, Presťahoval sa k vektoru vložka Aby zodpovedal svojmu pôvodu s koncom prvého. Výsledný vektor W Je čerpaný z pôvodu alebo do konca vložka, Tvorba trojuholníkovej postavy: trojuholník. Preto sa v tomto osobitnom prípade tento postup nazýva Trojuholník.

Všimnite si dôležitý detail, veľkosť alebo modul výsledného vektora nie je súčet modulov ďalších vektorov. V skutočnosti je to takmer vždy menšie, pokiaľ vektory nie sú rovnobežné.

Pozrime sa nižšie, čo sa stane v tomto prípade.

Špeciálny prípad: súčet paralelných vektorov

Opísaná metóda sa môže použiť aj na osobitný prípad, v ktorom sú vektory rovnobežné. Zvážte nasledujúci príklad:

Môže vám slúžiť: Boltzmann Constant: História, rovnice, výpočet, cvičeniaSúčet paralelných vektorov. Zdroj: f. Zapata.

Vektor zostáva vložka Vo svojej pôvodnej polohe a presúva sa k vektoru alebo takým spôsobom, že jeho pôvod súhlasí s koncom roku  vložka. Teraz je vektor čerpaný z pôvodu vložka A koniec alebo.

Toto je výsledný vektor W a jeho veľkosť je súčet veľkostí reklám. Smer a smer troch vektorov sú rovnaké.

Výsledný vektor má maximálny modul, ak doplnky tvoria uhol 0 °, ako napríklad v prípade príkladu. Ak vektory tvoria uhol 180 ° navzájom, výsledný vektor má minimálny modul.

Príklady súčtu vektorov

- Výstrahy

Cyklista cestuje prvé 3 km smerujúce na sever a potom 4 km západne. Vaše posunutie, ktoré voláme R, Ľahko sa nachádza s metódou trojuholníka plus referenčný systém, kde sú označené kardinálne body:

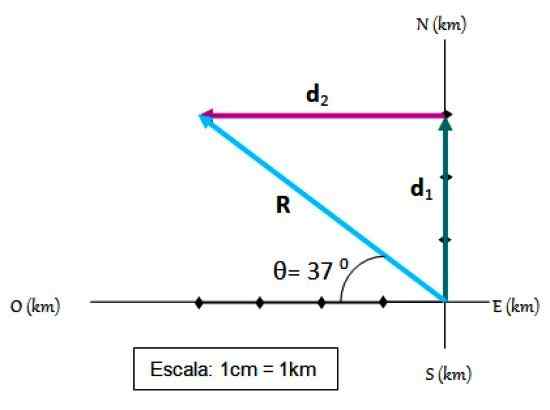Vyplývajúce z dvoch posunov. Zdroj: f. Zapata.

Kroky na pridanie vektora

-Východiskový bod sa zhoduje s pôvodom referenčného systému.

-Na súradnicových osiach je vybraná stupnica, ktorá je v tomto prípade 1 cm = 1 km

-Prvý posun je nakreslený na stupnici d_1.

-Potom d₁ Vytiahne sa druhý posun d₂, Tiež na stupnici.

-Výsledné posun R Je to vektor, ktorý prechádza z pôvodu do konca d₂.

-Veľkosť R Meria sa s odstupňovaným pravidlom, je ľahké overiť, či r = 5.

-Nakoniec uhol, ktorý R Forma s vodorovnou farbou sa meria pomocou transportéra a ukázalo sa, že je 9 = 37 ⁰

- Výsledná rýchlosť

Plavec chce prejsť cez rieku a za to nič rýchlosťou 6 km/h, kolmo na pobrežie, ale prúd, ktorý nesie rýchlosť 4 km/h.

Môže vám slúžiť: ohm: opatrenia odporu, príklady a vyriešené cvičenie

Ak chcete poznať svoju výslednú rýchlosť, pridávajú sa vektory rýchlosti plavca, ktoré boli nakreslené vertikálne a prúd, čo je horizontálne.

Podľa grafickej metódy sa získa výsledná rýchlosť vložka_R:

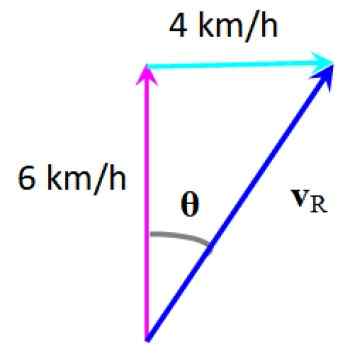Výsledná rýchlosť. Zdroj: f. Zapata.

Odchýlka, ktorú zažíva plavec, sa dá vypočítať podľa:

9 = arctg (4/6) = 33.7. napravo od vašej pôvodnej adresy

Veľkosť jeho rýchlosti sa zvyšuje, pretože rýchlosť rieky vekerne dodáva. Nájdete mierku opatrne, ako v predchádzajúcom príklade.

Alebo s pomocou trigonometrických dôvodov 33.7.:

Sen 33.7. = 4/v_R

vložka_R = 4/ sin 33.7. = 7.21 km/h

Cvičenie

Na častice sa konajú nasledujúce sily, ktorých veľkosti sú uvedené nižšie:

F₁= 2.5 n; F₂= 3 n; F₃= 4 n; F₄= 2.5 n

Nájdite výslednú silu.

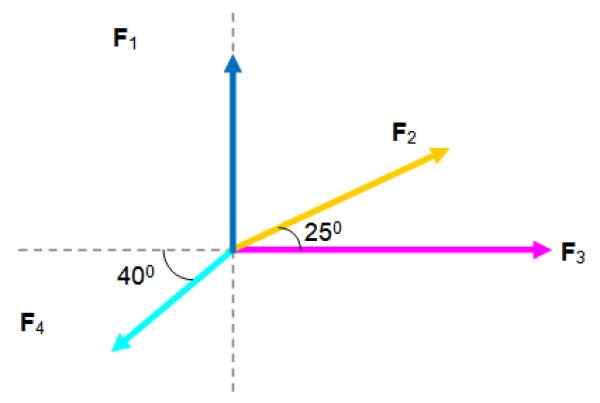Systém koplarných síl. Zdroj: f. Zapata.

Riešenie

Môžeme graficky pridať počnúc niektorým z vektorov, pretože vektorová suma je komutatívna.

Na obrázku A začal s F₁. Zriadenie stupnice a pomocou pravidla a tímu sa ostatné vektory prenášajú, aby ich umiestnili jeden po druhom.

Vektor F_R je nasmerovaný z pôvodu F₁ do konca F₄. Jeho veľkosť je 5.2 n a tvorí uhol 26.5. vzhľadom na vodorovné.

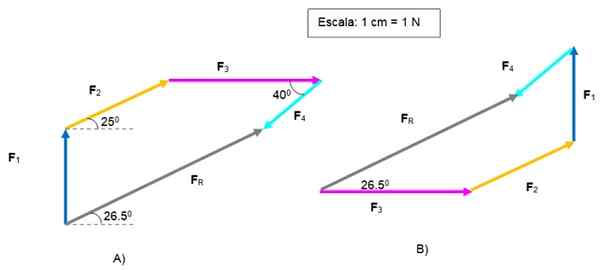Vektorový grafický súčet. Zdroj: f. Zapata.

Na obrázku B bol vyriešený rovnaký problém, počnúc s F₃ a končí F₄, Získať to isté F_R .

Polygóny sú rôzne, ale výsledok je rovnaký. Čitateľ môže znova otestovať poradie vektorov.

Odkazy

1. Bauer, w. 2011. Fyzika pre inžinierstvo a vedy. Zväzok 1. MC Graw Hill.
2. Bedford, 2000. Do. Mechanika pre inžinierstvo: statické. Addison Wesley.
3. Figueroa, D. (2005). Séria: Fyzika pre vedu a inžinierstvo. Zväzok 1. Kinematika. Editoval Douglas Figueroa (USB).
4. Giambattista, a. 2010. Fyzika. Druhý. Edimatizovať. McGraw Hill.
5. Sears, Zemansky. 2016. Fyzika univerzity s modernou fyzikou. 14. Edimatizovať. Zväzok 1.