Charakteristiky minimálnej ceny, výhody, nevýhody

On Metóda minimálnych nákladov Je to postup, ktorý sa používa na získanie počiatočného uskutočniteľného riešenia pre dopravný problém. Používa sa, keď je prioritou zníženie distribučných nákladov výrobkov.

Metóda minimálnych nákladov sa snaží dosiahnuť najnižšie náklady na dopravu medzi niekoľkými centrami dopytu (destinácie) a niekoľkými dodávateľskými centrami (zdroje).

Zdroj: Pixabay.com

Výrobná kapacita alebo dodávka každého zdroja, ako aj požiadavka alebo dopyt po každom cieľovom mieste, sú známe a fixované.

Náklady na prepravu jednotky produktu sú známe aj z každého zdroja do každého cieľa.

Produkt sa musí prepravovať z niekoľkých zdrojov do rôznych destinácií takým spôsobom, aby sa uspokojil dopyt z každého cieľa a zároveň minimalizoval celkové dopravné náklady.

Ak je prioritou úspora času, namiesto úspory nákladov je možné použiť iné metódy.

[TOC]

Charakteristika

Optimálne pridelenie produktu z rôznych zdrojov do rôznych destinácií sa nazýva problém s dopravou.

- Prepravné modely sa zaoberajú výrobkom vyrobeným v rôznych závodoch alebo továrňach (zdroje dodávok) niekoľkým skladom (destinácie dopytu).

- Cieľom je splniť požiadavky destinácií v rámci obmedzení výrobnej kapacity rastlín, na minimálne náklady na dopravu.

Kroky metódy minimálnych nákladov

Krok 1

Bunka obsahujúca najnižšie prenosové náklady na celú tabuľku je vybraná. Táto bunka je pridelená čo najviac jednotiek. Táto suma môže byť obmedzená obmedzeniami ponúk a požiadaviek.

V prípade, že niekoľko buniek má najnižšie náklady, bude vybraná bunka, kde sa dá vykonať maximálna alokácia.

Môže vám slúžiť: Analytický postup (účtovníctvo)

Potom pokračujeme v úprave ponuky a dopytu, ktorý je v postihnutom riadku a stĺpci. Je upravený odpočítaním množstva priradeného k bunke.

Krok 2

Riadok alebo stĺpec, v ktorom je vyčerpaný (buď nula), dodávka alebo dopyt sa eliminuje.

V prípade, že hodnoty, ponuka a dopyt, či už sa rovnajú nule, je možné ľubovoľne eliminovať akýkoľvek riadok alebo stĺpec.

Krok 3

Predchádzajúce kroky sa opakujú s nasledujúcimi nižšími nákladmi a pokračujú, kým celá ponuka dostupná v rôznych zdrojoch alebo všetky dopyt po rôznych destináciách.

Žiadosti

- Minimalizujte náklady na dopravu tovární na sklady alebo sklady do maloobchodných predajní.

- Určite minimálne umiestnenie nákladov novej továrne, skladu alebo predajnej kancelárie.

- Určite harmonogram minimálnej výroby nákladov, ktorý spĺňa dopyt spoločnosti s výrobnými obmedzeniami.

Výhody

Metóda minimálnych nákladov sa považuje za výsledky presnejších a optimálnejších výsledkov v porovnaní s výsledkami severozápadného rohu.

Dôvodom je, že metóda severozápadného rohu predstavuje iba dôležitosť požiadavky na dodanie a dostupnosť, pričom ľavý horný roh ako počiatočné priradenie, bez ohľadu na prepravné náklady.

Na druhej strane metóda minimálnych nákladov zahŕňa náklady na dopravu, zatiaľ čo sa úlohy vykonávajú.

- Na rozdiel od metódy Northwest Corner táto metóda poskytuje presné riešenie, pretože zvažuje náklady na dopravu pri vykonávaní alokácie.

- Metóda minimálnych nákladov je veľmi jednoduchá metóda použitia.

Môže vám slúžiť: Organizácia obchodnej spoločnosti: pozície a funkcie

- Je veľmi jednoduché a ľahké vypočítať optimálne riešenie touto metódou.

- Metóda minimálnych nákladov je veľmi ľahko pochopiteľná.

Nevýhody

- Na získanie optimálneho riešenia sa musia dodržiavať určité pravidlá. Metóda minimálnych nákladov ich však nedodržiava krok za krokom.

- Metóda minimálnych nákladov sa nedodržiava žiadne systematické pravidlo, keď je v minimálnych nákladoch kravata.

- Metóda minimálnych nákladov umožňuje výber prostredníctvom pozorovania personálu, ktorý by mohol vytvoriť nedorozumenia na získanie optimálneho riešenia.

- Nemá schopnosť poskytnúť žiadne kritériá, ktoré umožní určiť, či riešenie dosiahnuté touto metódou je alebo nie je najoptimálnejšie.

- Sumy ponúk a požiadaviek sú vždy rovnaké, pretože sa v priebehu času nemenia.

- Nezohľadňuje priradenie iných typov faktorov, ale iba náklady na dopravu.

Príklad

Koncept metódy minimálnych nákladov môžete pochopiť prostredníctvom nasledujúceho problému:

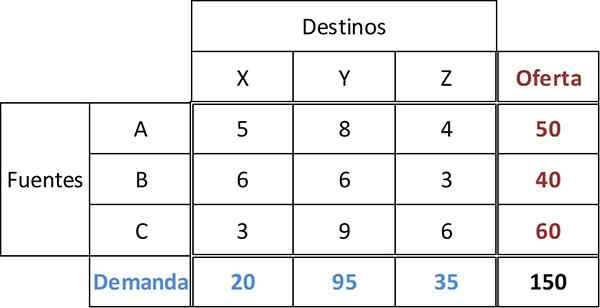
V tejto tabuľke je ponuka každého zdroja A, B, C 50, 40 a 60 jednotiek. Dopyt po troch maloobchodných x, y, z, je 20, 95 a 35 jednotiek. Pre všetky trasy sa vyskytujú náklady na dopravu.

Minimálne náklady na dopravu je možné získať podľa krokov uvedených nižšie:

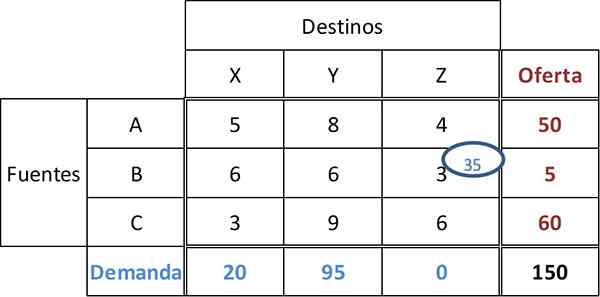
Minimálne náklady v tabuľke sú 3, s kravatou v bunkách BZ a CX. Všeobecne platí, že na získanie najlepšieho počiatočného riešenia je možné zvoliť náklady, ak je možné priradiť najväčšiu sumu.

Môže vám slúžiť: splatné dokumenty

Preto bude 35 jednotiek priradených k bunke BZ. Preto je spokojný dopyt po maloobchode z a ponecháva 5 jednotiek vo Fuente B.

Vysvetlenie metódy

Minimálne náklady sú opäť 3. Preto bude 20 jednotiek priradených k bunke CX. Takto je splnený dopyt po maloobchode X a ponecháva 40 jednotiek na Fuente C.

Nasledujúce minimálne náklady sú 4. Dopyt po Z je však už dokončený. Ide o ďalšie minimálne náklady, ktoré je 5. Tiež bol dokončený dopyt X.

Ďalšie minimálne náklady sú 6, s remízou medzi tromi bunkami. Jednotky však nemožno priradiť k bunkám BX a CZ, pretože dopyt po maloobchode X a Z je uspokojený. Potom je do bunky priradených 5 jednotiek. Dodávka zdroja B je teda dokončená.

Ďalšia minimálna cena je 8, priraďuje 50 jednotiek do bunky AY, čím dokončuje dodávku zdroja.

Nasledujúce minimálne náklady sú 9. K Cy bunke je pridelených 40 jednotiek, čím sa dokončí dopyt a ponuka všetkých destinácií a zdrojov. Výsledné konečné priradenie je:

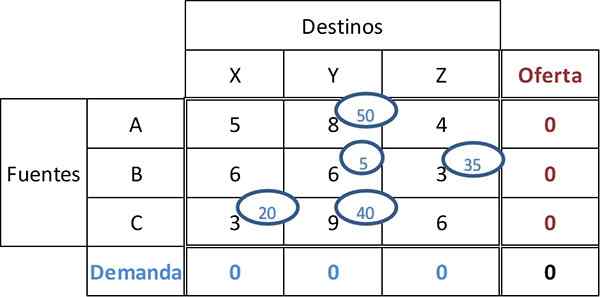
Celkové náklady sa môžu vypočítať vynásobením množstiev priradených nákladmi zodpovedajúcich buniek: celkové náklady = 50*8 + 5*6 + 35*3 + 20*3 + 40*9 = 955.

Odkazy

1. Business Jargons (2019). Metóda najmenej nákladov. Zobraté z: podnikateľov.com.
2. Poradenstvo prideľovania (2019). Pomoc priradenia metódy najmenej nákladov. Zobraté z: priradenie.com.
3. Business Management (2015). Problém. Zobraté z: inžinierskych-bakalárskych stupňov.com.
4. Josefina Pacheco (2019). Aká je metóda minimálnych nákladov? Web a spoločnosti. Prevzaté: WbyEmepresas.com.
5. Atozmath (2019). Príklad najmenej nákladovej metódy. Prevzaté z: CBOM.Atozmath.com.