Rovnomerne zrýchlené charakteristiky priamočiarého pohybu, vzorce

On rovnomerne zrýchlený priamy pohyb Je to ten, ktorý prechádza cez priamku a v ktorej mobil zvyšuje alebo znižuje svoju rýchlosť konštantnou rýchlosťou. Táto rýchlosť je veľkosť, ktorá opisuje rytmus, s ktorým sa rýchlosť mení a nazýva sa zrýchlenie.

V prípade rovnomerne zrýchleného alebo rozmanitého priameho pohybu (MRUV) je konštantné zrýchlenie zodpovedné za zmenu veľkosti rýchlosti. V iných typoch pohybu je zrýchlenie tiež schopné zmeniť smer a pocit rýchlosti alebo dokonca zmeniť smer, ako v rovnomernom pohybe kruhového pohybu.

postava 1. Zrýchlené pohyby sú najčastejšie. Zdroj: Pixabay.

Pretože zrýchlenie predstavuje zmenu rýchlosti v priebehu času, jej jednotky v medzinárodnom systéme sú M/s² (metrov na sekundy na druhú). Rovnako ako rýchlosť, zrýchlenie môže byť ocenené pozitívnym alebo negatívnym znakom, keď sa rýchlosť zvyšuje alebo klesá.

Zrýchlenie hovoria o +3 m/s² To znamená, že na každú sekundu, ktorá prechádza, sa mobilná rýchlosť zvyšuje o 3 m/s. Ak na začiatku pohybu (pri t = 0) bola mobilná rýchlosť +1 m/s, potom po sekundu bude 4 m/s a po 2 sekundách bude 7 m/s.

V rovnomerne rozmanitom priamom pohybe sa berú do úvahy výmeny rýchlosti, ktoré mobilné objekty denne majú. Je to realistickejší model ako model rovnomerného priameho pohybu. Stále je to stále dosť obmedzené, pretože obmedzuje mobil na cestu iba na priamke.

[TOC]

Charakteristika

Toto sú hlavné charakteristiky rovnomerne zrýchleného priamočiarého pohybu:

-Pohyb vždy prechádza po priamke.

-Zrýchlenie mobilu je konštantné, a to v rozsahu aj v smere a význame.

-Mobilná rýchlosť sa zvyšuje (alebo znižuje) lineárne.

-Od zrýchlenia do Postupom času zostáva konštantný tón, Graf jeho veľkosti ako funkcia času je priamka. V príklade znázornenom na obrázku 2 je čiara modrá a hodnota zrýchlenia sa načíta na vertikálnej osi, približne +0.68 m/s².

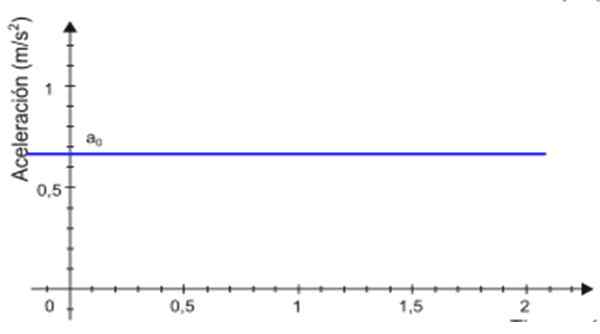Obrázok 2. Graf zrýchlenia podľa času pre rovnomerne rozmanitý priamy pohyb. Zdroj: Wikimedia Commons.

-Rýchlostná tabuľka vložka o tón Je to priamka (v zelenej na obrázku 3), ktorej sklon je rovnocenný s mobilným zrýchlením. V príklade je sklon pozitívny.

Môže vám slúžiť: bór nitrid (BN): štruktúra, vlastnosti, získanie, použitia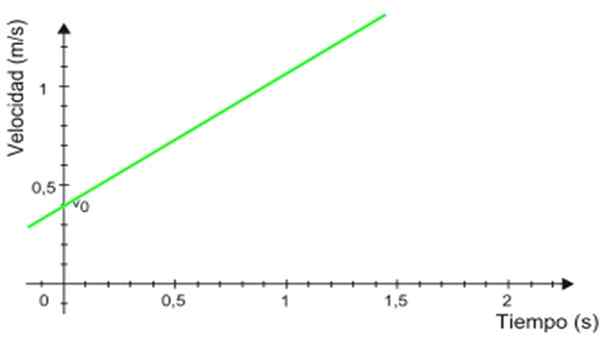 Obrázok 3. Rýchlostný graf založený na čase pre rovnomerne rozmanitý priamy pohyb. Zdroj: Wikimedia Commons.

-Rez s vertikálnou osou označuje počiatočnú rýchlosť, v tomto prípade je 0.4 m/s.

-Nakoniec graf polohy X verzus čas je krivka znázornená červenou na obrázku 4, čo je vždy podobenstvo.

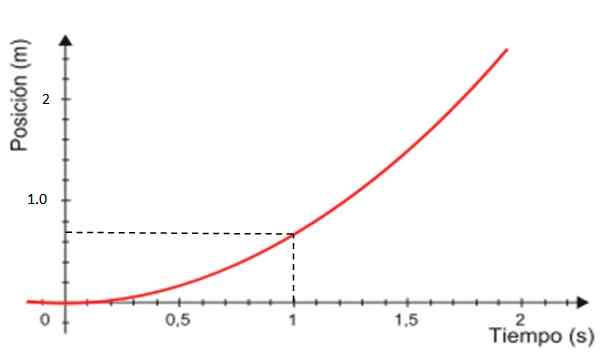Obrázok 4. Grafika polohy založená na čase pre rovnomerne rozmanitý priamy pohyb. Zdroj: Upravené Wikimedia Commons.

Vzdialenosť prešla z grafu v vs. tón

Tým, že má graf V vs. t, výpočet vzdialenosti prevezenej mobilom je veľmi jednoduchý. Cesta vzdialená je rovnocenná s oblasťou pod vedením, ktorá je zahrnutá v požadovanom časovom intervale.

V zobrazenom príklade predpokladajme, že chcete poznať vzdialenosť prejdená mobilom medzi 0 a 1 sekundou. Použitím tohto grafu pozri obrázok 5.

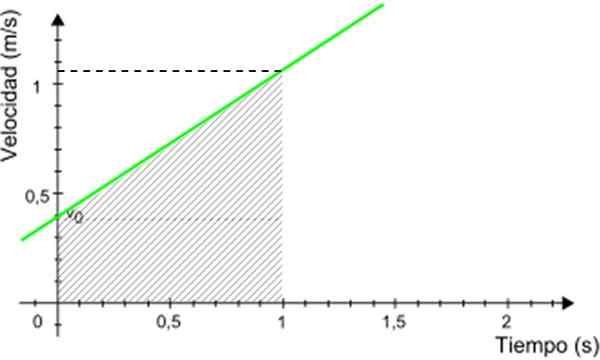Obrázok 5. Graf na výpočet vzdialenosti prejdenej mobilom. Zdroj: Upravené Wikimedia Commons.

Vzdialenosť hľadala numericky rovnocennú s plochou tieňovaného lichobežníka na obrázku 3. Oblasť lichobežníka je daná: (Hlavná základňa + menšia základňa) x výška/2

Prejdená vzdialenosť = (0.4 + 1.05) x 1/2 m = 0.725 m

Je tiež možné rozdeliť tieňovanú oblasť na trojuholník a obdĺžnik, vypočítať zodpovedajúce oblasti a pridať ich. Prejdená vzdialenosť je pozitívna, aj keď častica ide doprava alebo doľava.

Vzorce a rovnice

Priemerné zrýchlenie aj okamžité zrýchlenie majú v MRUV rovnakú hodnotu, preto:

-Zrýchlenie: do = konštantný

Keď sa zrýchlenie rovná 0, pohyb je rovnomerný priamy, pretože rýchlosť by bola v tomto prípade konštantná. Znak do Môže to byť pozitívne alebo negatívne.

Pretože zrýchlenie je sklon čiary V oproti T, rovnica V (t) je:

-Rýchlosť v závislosti od času: v (t) = v_ani + Na

Kde vložka_ani Je to počiatočná hodnota mobilnej rýchlosti

-Pozícia v závislosti od času: x (t) = x_ani + vložka_ani T +½t² 

Ak nie je k dispozícii čas, ale namiesto toho existujú rýchlosti a posuny, existuje veľmi užitočná rovnica, ktorá sa získa vyčistením času v (t) = v_ani + Na a nahradenie v poslednej rovnici. Je o:

Môže vám slúžiť: Potenciálna energia: Charakteristiky, typy, výpočet a príklady

-Rovnica, ktorá neobsahuje čas: vložka² = v_ani² +2.do.ΔX

Vyriešené cvičenia

Pri riešení kinematického cvičenia je dôležité zabezpečiť, aby sa navrhovaná situácia prispôsobila modelu, ktorý sa má použiť. Napríklad rovnice rovnomerného priameho pohybu nie sú platné pre zrýchlený pohyb.

A tie zrýchleného pohybu nie sú platné napríklad pre kruhový alebo zakrivený pohyb. Prvý z týchto cvičení vyriešených nižšie kombinuje dve mobily s rôznymi pohybmi. Na správne vyriešenie je potrebné ísť na príslušný model pohybu.

-Cvičenie vyriešené 1

Ak chcete zistiť hĺbku studne, dieťa vynechá mincu a súčasne aktivuje svoje stopky, ktoré sa presne zastaví pri počúvaní menového prevratu proti vode. Jeho čítanie bolo 2.5 sekúnd. S vedomím, že rýchlosť zvuku vo vzduchu je 340 m/s, vypočítajte hĺbku studne.

Riešenie

Byť h Hĺbka studne. Mena prechádza touto vzdialenosťou vo voľnom páde, rovnomerne rôznym vertikálnym pohybom, s počiatočnou rýchlosťou 0, pretože mena klesá a konštantné zrýchlenie dole rovnaké ako 9.8 m/s². Venovať sa tón_m Pri tom.

Akonáhle sa mena zrazí s vodou, zvuk spôsobený kliknutím prechádza do ucha dieťaťa, ktorý pri počúvaní zastaví stopky. Neexistujú dôvody domnievať sa, že rýchlosť zvuku sa mení pri lezení do studne, takže pohyb zvuku je rovnomerný priamy priamy. Zvuk si vyžaduje čas tón_siež osloviť dieťa.

Pohybová rovnica pre menu:

H = ½.g.tón_m ² = 4.9 t_m ²

Kde boli vymenené X a do rovnice pre pozíciu uvedenú v predchádzajúcej časti h a g.

Rovnica zvukovej pohybu:

h = v_siež . tón_siež = 340 t_siež

Toto je známa rovnica Vzdialenosť = rýchlosť x čas. S týmito dvoma rovnicami existujú tri neznáme: H, TM a TS. Pre časy existuje vzťah, je známe, že všetko trvá 2.5 sekúnd, preto:

tón_m + tón_siež = 2.5 s

Vyrovnať obe rovnice:

4.9 t_m ² = 340 t_siež

Vyčistenie jedného z časov a výmena:

4.9 t_m ²= 340.(2.5 - T_m)

Pri vývoji termínu práva a transponovania sa získa:

Môže vám slúžiť: vertikálny záber: vzorce, rovnice, príklady

4.9 t_m ²+340 t_m - 850 = 0

Toto je rovnica druhého stupňa s dvoma riešeniami: 2.416 a -71.8. Pozitívne riešenie je vybrané, čo má zmysel, pretože čas nemôže byť negatívny av žiadnom prípade musí byť menší ako 2.5 sekúnd. Za túto dobu sa získa nahradením hĺbky studne:

4.9 t_m ²= 4.9 x 2.416² M = 28.6 m

-Cvičenie vyriešené 2

Auto, ktoré sa pohybuje rýchlosťou 90 km/h, sa blíži k priečnej ceste s semafor. Keď je tam 70 m, zapnuté žlté svetlo, ktorého trvanie je 4 sekundy. Vzdialenosť medzi semaforom a ďalším rohom je 50 m.

Vodič má tieto dve možnosti: a) stáť na - 4 m/s² alebo b) zrýchliť pri + 2 m/s². Ktorá z týchto dvoch možností umožňuje vodičovi zastaviť sa alebo prekročiť celú cestu skôr, ako sa svetlo zmení na červenú?

Riešenie

Počiatočná poloha vodiča je x = 0 práve vtedy, keď vidí žlté svetlo. Je dôležité správne previesť jednotky: 90 km/h sa rovná 25 m/s.

Podľa možnosti A), za 4 sekundy, ktoré žlté svetlo vydrží, vodič prechádza:

x (t) = v_ani T +½t²= 25.4 -½.(-4).4²M = 68 m (2 metre pred semaforom)

Analýza možnosti B) máte:

x (t) = v_ani T +½t²= 25.T +½.2.tón²

Zatiaľ čo žlté svetlo trvá, vodič putuje týmto spôsobom:

x = 25.4 +½.2.4²M = 116 m

Ale 116 m je menšia ako vzdialenosť, ktorá je k dispozícii na dosiahnutie nasledujúceho rohu, čo je 70 + 50 m = 120 m, preto nedokáže prekročiť celú ulicu skôr, ako sa zapne červené svetlo. Odporúčaná akcia je zastaviť a zostať 2 metre od semaforu.

Žiadosti

Každý deň ľudia zažívajú účinky zrýchlenia: keď cestujú autom alebo autobusom, pretože neustále sa musia zastaviť a zrýchliť, aby prispôsobili pochod na prekážky cesty. Zrýchlenie sa tiež vyskytuje, keď ide hore alebo dole vo výťahu.

Zábavné parky sú stránky, v ktorých ľudia platia za zažívanie účinkov zrýchlenia a baviť sa.

V prírode sa pozoruje rovnomerne rozmanitý priamy pohyb, keď je objekt voľne spadnutý alebo keď sa vyhodí zvisle nahor a očakáva sa, že sa vráti na zem. Ak je odpor vzduch opovrhuje, hodnota zrýchlenia je hodnota gravitácie: 9.8 m/s2.

Odkazy

1. Bauer, w. 2011. Fyzika pre inžinierstvo a vedy. Zväzok 1. MC Graw Hill.40-45.
2. Figueroa, D. Fyzická séria pre vedu a inžinierstvo. Zväzok 3. Vydanie. Kinematika. 69-85.
3. Giancoli, D.  Fyzika: Princípy s aplikáciami. 6^th. Ed Prentice Hall. 19-36.
4. Hewitt, Paul. 2012. Koncepčná fyzická veda. 5^th. Edimatizovať. Pearson. 14-18.
5. Kirkpatrick, L. 2007. Fyzika: pohľad na svet. 6^{ubytovať sa} Skrátene vydanie. Učenie sa. 15-19.
6. Wilson, J. 2011. Fyzika 10. Pearson Vzdelanie. 116-119