Eliptický pohyb

Aký je eliptický pohyb?

V eliptickom pohybe mobil opisuje elipsu, ako to robia planéty okolo slnka a Mesiac a umelé satelity okolo Zeme, aby sme spomenuli niektoré príklady rodiny.

Sila, ktorá vedie k tomuto pohybu, je sila gravitácie, centrálna sila. Tento druh síl je smerovaný k (alebo z) pevného bodu alebo a jeho modul závisí od vzdialenosti od tohto bodu. Ak R je vzdialenosť a alebo_r Je to jednotkový vektor v smere rádio, centrálna sila F Je to vektorová funkcia formulára:

F = F (r) alebo_r

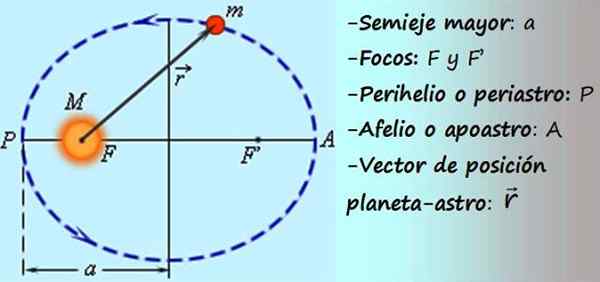
postava 1. Schéma eliptického pohybu planéty okolo slnka. Zdroj: f. Zapata.

S nejakou matematikou je možné ukázať, že pohyb objektu pod pôsobením gravitácie sleduje niektoré z týchto štyroch trajektórií: elipsa, obvod, hyperbola alebo podobenstvo.

Charakteristiky eliptického pohybu

Niektoré z hlavných charakteristík eliptického pohybu pod centrálnou silou sú:

-Uhlová hybnosť sa zachováva s ohľadom na O, nazývaná L a to sa vypočíta prostredníctvom vektorového produktu medzi vektormi polohy a rýchlosti: L = r × mvložka, Kde m predstavuje hmotnosť mobilného objektu.

-Eliptická obežná dráha leží v rovine určenej vektormi r a vložka.

-Hovor je odvodený z uhlovej hybnosti Zákon, ktorý stanovuje, že mobilný mobilný priestor v rovnakých časoch cestuje.

-Mechanická energia sa zachováva aj v eliptickom pohybe, ak neexistujú žiadne disipatívne sily.

-Čas oneskorenia mobilu pri poskytovaní obežnej dráhy a celkovej energie, závisí iba od dĺžky „A“ hlavného semi -hexiku elipsy.

Rozdiely s kruhovým pohybom

Aj keď v kruhovom aj eliptickom pohybe, objekt sa pohybuje v uzavretej a opakujúcej sa trajektórii, to znamená pravidelné, existujú zjavné rozdiely medzi jedným pohybom a druhým, napríklad: napríklad:

Môže vám slúžiť: Nortonova veta: popis, aplikácie, príklady a cvičenia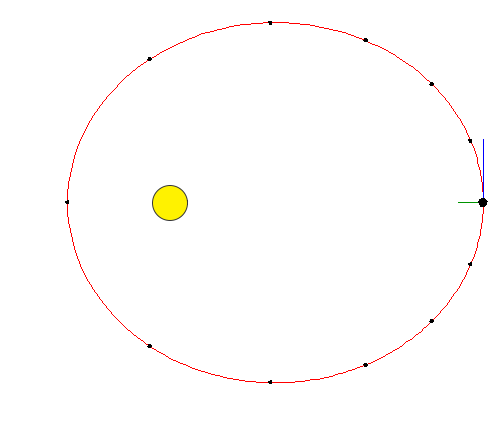Obrázok 2.- Rýchlosť je maximálna, keď je vzdialenosť od slnka minimálna. Zdroj: Wikimedia Commons.

-V kruhovom pohybe mobil opisuje obvod, ktorého polomer (vzdialenosť od stredu trajektórie) je konštantný, zatiaľ čo v eliptickom pohybe opisuje elipsa, v ktorej je vzdialenosť od stredu trajektórie variabilná (pozri obrázok 1).

-V prípade rovnomerného pohybu kruhového pohybu MCU Mobile Barr. Toto je zákon oblastí, známy tiež ako Keplerov druhý zákon planetárneho hnutia.

Dôležité rovnice planétového eliptického hnutia

Obdobie

V eliptickom pohybe odvodenom z gravitačnej príťažlivosti je t -perióda pohybu čas, ktorý potrebuje na planétu alebo satelit (m), aby opísal eliptické kolo okolo slnka alebo Zeme (m). Uplatňovanie zachovania energie z toho vyplýva, že je úmerná kocke dĺžky najväčšej semifinále elipsy:

Kde g je univerzálna gravitačná konštanta: 6.67 × 10^-jedenásť N ∙ m²/kg²,   M je hmotnosť slnka, Zem alebo príčina interakcie na M a „A“ je dĺžka hlavnej semi -osi.

Mechanická energia

Celková energia pre planétový systém (M)- Slnko (M) je:

Uhlová hybnosť

Rozsah uhlovej hybnosti v bode eliptickej obežnej dráhy tiež závisí od dĺžky hlavnej semi -osi, ako aj od excentricity „E“, bezrozmerného parametra, ktorý naznačuje, ako je lichotený elipou. Ak e = 0, elipsa sa stáva obvodom.

Môže vám slúžiť: Leyden fľaša: časti, prevádzka, experimenty

Rýchlosť

Veľkosť rýchlosti je daná nasledujúcou rovnicou:

Kde r je vzdialenosť medzi orbitom bodom (umiestnenie planéty) a zaostrením (slnko).

Príklady eliptického pohybu

Planetárne pohyby

Prvý zákon Keplera naznačuje, že pohyb planét okolo slnka sleduje eliptickú trajektóriu, so slnkom v jednom z bodových reflektorov. Niektoré kométy, ktoré pravidelne navštevujú Zem, napríklad Comet Halley tiež sledujú eliptický pohyb.

Okrem tohto eliptického translačného pohybu a pohybu rotácie okolo ich osi majú planéty svoje vlastné pohyby v dôsledku komplexných gravitačných interakcií s ostatnými nebeskými planétami a telami slnečnej sústavy. Týmto spôsobom sú pohyby precesie a nutívy, ktoré má Zem a ktoré sú spôsobené kĺbovou gravitačnou príťažlivosťou slnka a mesiaca.

V precesii je os Zeme opisuje kužeľ pri otáčaní okolo osi kolmá na plán alebo ekliptický. A pri nutácii, ktorá sa prekrýva s precesiou, os Zeme osciluje hore a dole a každých 18 opisuje eliptickú slučku.6 rokov. Celkovo 1385 z týchto slučiek za 25767 rokov, čo je obdobie precesie Zemickej osi.

Častica pre oceánsku vodu

V oceánskych vodách častíc vykonáva eliptický pohyb, pričom elipsa stále viac a viac lichotí zvyšovaním hĺbky. Na druhej strane, keď sú vody hlboké, pohyb častíc je kruhový.

Čo sa stane, je to, že keď sa vlna priblíži k pobrežiu, trenie sily sa objavia vďaka blízkosti k dne a toto trenie musí spomaliť pohyb v dolnej časti trajektórie, zatiaľ čo hrebeň pokračuje vo svojom pohybe.

Môže vám slúžiť: Rovnomerný priamy pohyb: Charakteristiky, vzorce, cvičenia

Výsledkom je, že obvod je zásobený a účinok je zvýraznený, keď sa zvyšuje hĺbka.

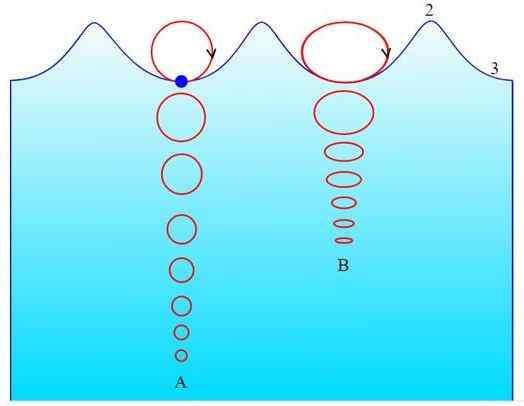Obrázok 3. Pohyb oceánskych vĺn v: a) hlboké vody a b) povrchové vody. Zdroj: Wikimedia Commons.

Režim eliptického kmitania vo fyzickom kyvadle

Fyzikálne kyvadlo pozostáva z tuhej pevnej látky, ktorá môže oscilovať v rovine okolo osi kolmej na ňu. Ak sa objekt môže pohybovať s úplnou slobodou, môžete opísať akýkoľvek uhol okolo osi, ktorý spája stred hmotnosti pomocou suspenzného bodu, ako aj otáčanie okolo neho.

Vďaka rotácii Zeme je kyvadlo schopné opísať obežné dráhy približne elipticky, ktoré sú známe ako eliptický oscilačný režim, ktorý sa vyznačuje uhlovou hybnosťou odlišnou od 0.

K dispozícii je tiež plochý režim (uhlová hybnosť) a kužeľový režim (iný uhlový moment.

Eliptické bicykle

Eliptické pohyby opísané skôr sa vyskytujú v prírode, ale môžu sa tiež použiť na výrobu užitočných gadgetov, ako sú eliptické bicykle, ktoré sú veľmi populárnymi strojmi na vykonávanie aeróbnych cvičení.

Sú to pevné bicykle, ktoré v podstate pozostávajú z riadidla a dvoch pedálov, ktoré osoba pôsobí pri propagácii s ich váhou, opisujúc nohami elipsou. Je to prirodzený a nízko nárazový pohyb, ktorý je prospešný, pretože pohybuje mnohými skupinami svalov po celom tele.

Odkazy

1. Astronómia pre všetkých. Precesia a nutácia. Získané z: Astronomiapararatodos.com.
2. Výpočet rýchlosti na eliptickej obežnej dráhe. Obnovené z: fóra.Logary.com.
3. Fowler, Michael. Eliptické obežné dráhy: Cesty k planétou. Získané z: Galileo.Fyzický.Virgínia.Edu.
4. Hernández, J. Štúdium režimov oscilácie v symetrickom fyzickom kyvadle s použitím efektívneho potenciálu. Získané z: SCIELO.orgán.co.
5. Kittel, C. 1973. Mechanika. Kurz fyziky Berkeley. Zväzok 1. Edimatizovať. Obrátil som sa.
6. Eliptická obežná dráha pod pôsobením centrálnej sily. Zdroj: SC.Ehu.je.
7. Konzervatívne systémy. Obnovené z: DFMF.Udelený.je.Wikipedia. Eliptická obežná dráha. Zdroj: In.Wikipedia.orgán.