Tetradecágono

Čo je tetradecágono?

Tetradecágono je plochá a uzavretá geometrická postava 14 strán, ktorá patrí do rodiny polygónov. Je tiež známy pod názvom tetrakaidecágono, Všetky slová odvodené z gréckych slov: „tetra“ (cuatri), „kai“ (viac), „rozpad“ (desať) a „gon“ (uhol), pretože má tiež 14 vnútorných uhlov.

Obrázok ukazuje pravidelný tetradagon, to znamená, že všetky strany a vnútorné uhly majú rovnaké opatrenie, ktoré ukazujú hlavné charakteristiky tohto obrázku.

postava 1.- Pravidelná tetrade s hlavnými charakteristikami. Zdroj: f. Zapata.

Tetradekáno prvky

• Strany: Nazývajú sa 14 -riadkové segmenty, ktoré sú uzavreté, aby sa vytvorili obrázok. Všetci môžu mať rovnakú dĺžku, v takom prípade je polygón pravidelný, alebo sa môžu líšiť a potom existuje nepravidelná tetrade.
• Vrcholy: Sú priesečníky medzi následnými segmentmi a tetradecágono má 14 vrcholov.
• Stred: Rovnomerný bod vrcholov.
• Rádio: segment, ktorý spája stred vrcholom.
• Vnútorný: Je tvorená vnútornou časťou postavy a medzi dvoma po sebe idúcimi alebo susednými segmentmi. Opatrenia 154.286 ° pre pravidelný tetradecágon, bez ohľadu na veľkosť strany.
• Vonkajší uhol: vytvorené medzi jednou stranou a predĺžením jednej zo susedných strán. Bez ohľadu na dĺžku strany, tento uhol meria 25.7143 ° pre pravidelnú tetrade.
• Centrálny uhol: Ten, kto má svoj vrchol, ktorý sa zhoduje so stredom polygónu a jeho strany, sú dve po sebe idúce rádiá.
• Diagonálny: segment, ktorý spája dva nekontrolované vrcholy.

Ako je na tom tetradecágono?

Pravidelné polygóny N strany, ktoré sú vyrobené z pravidla a kompas majú N formulára 2^r p₁… P_{klimatizovať}, Byť p_Jo Fermat Primo sa líšia a zase Fermatove prvotné čísla majú tvar 2ⁿ + 1.

Môže vám slúžiť: Činnutie riadku: vzorec a rovnice, reprezentácia, príklady

Tetradecágono má n = 14 strán, ale 14 = 7 × 2, ktoré nie sú fermatskými bratrancami, pretože ich nemožno vyjadriť označeným spôsobom. Preto tento polygón nepriznáva presnú konštrukciu s pravidlom a kompasom, ale konštrukcia, ktorá sa blíži veľmi dobre, prostredníctvom niekoľkých metód.

Všeobecná metóda budovania bežných polygónov

Nasleduje všeobecná metóda (nie jediná), ktorá stavia pravidelné polygóny zaregistrované v obvode, vrátane bežnej tetrady.

Skladá sa z rozdelenia vertikálneho priemeru tohto obvodu na toľko rovnakých častí, koľko strán má polygón, ktorý má kresliť. V prípade TetradeCágono to bude 14 častí očíslovaných na obrázku 2. Toto sú kroky:

• Nakreslite vertikálny priemer z A do B.
• Potom nakreslite polo -pravú začatie od bodu A, otvorte kompas s ľubovoľným otvorením a urobte o ňom 14 rovnako rozmiestnených divízií. Semirrec a jeho divízie sa môžu dostať z obvodu.
• Pripojte sa k značke 14VA (v modrej na obrázku) na konci polo.
• Ak chcete pokračovať v pripojení k zvyškom značiek v polokreačnej farbe s príslušnými bodmi na vertikálnom priemere (zelené body).
• S špičkou kompasu v A a otváraní sa rovnajúcom sa miere priemeru obvodu je nakreslený oblúk. S rovnakým opatrením, ale podpora špičky v B (bod 14 z obrázku 2) je nakreslený ďalší oblúk, ktorý je rezaný prvým v bodoch v a v 'označených.

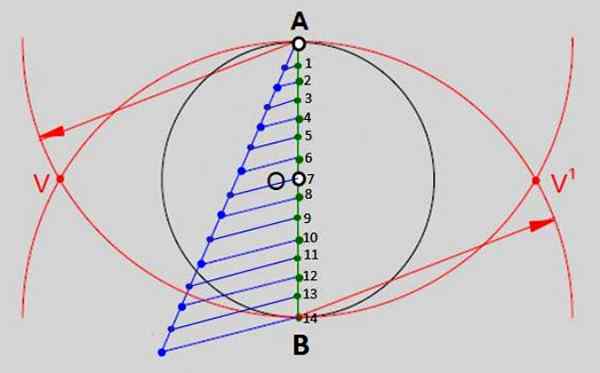Obrázok 2.- Jednou zo všeobecných metód na zostavenie pravidelných polygónov je rozdelenie priemeru obvodu na toľko rovnakých častí, koľko bokov má polygón. V prípade pravidelného tetradecha existuje 14 rovnakých častí. Zdroj: f. Zapata.

• Teraz, s pravidlom, nakreslite čiaru z V 'do bodu 2 a predĺžte ju, aby ste pretínali obvod v bode C na obrázku 3. Označte bod križovatky, ktorý bude jedným z vrcholov obrázku.

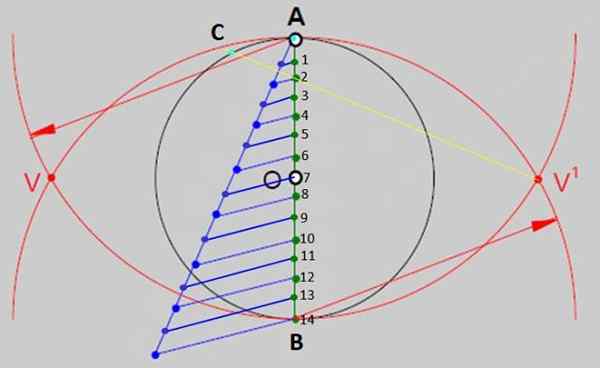Môže vám slúžiť: Štatistické vetvy Obrázok 3.- Segment striedavého prúdu je miera bokov postavenej tetradecionu. Zdroj: f. Zapata.

• Otvorte kompas v striedavej vzdialenosti a podoprenie špičky v A alebo C, kreslenie oblúkov rovnakej miery počas celého obvodu, týmto spôsobom je rozdelený na približne rovnaké časti, križovatky medzi oblúkmi a obvodom sú vrcholy vrcholy tetradecágono.
• S pravidlom sa pripojte k vrcholom s segmentmi čiary a vytvorte strany mnohouholníka.
• Opatrne vymažte pomocné konštrukcie.

V nasledujúcej animácii je uvedená ďalšia približná metóda, s pravidlom a kompasom:

Obrázok 4.- Animácia, ktorá ukazuje, ako sa vyrába Tetradecagon (približne pravidelný polygón). Zdroj: Wikimedia Commons.

Vzorce pre pravidelnú tetrade

Pre bežné polygóny sú platné nasledujúce vzorce:

• Číslo listu: n
• Vedľajšie opatrenie: a
• Apothém: L_Do
• Rádio: R
• Obvod: P
• Oblasť: a
• Vnútorný uhol: i
• Vonkajší uhol: e
• Diagonálne: D

Známa strana apothém

A = 2L_Do × TG (π/n)

Pre n = 14:

A = 2L_Do × TG (π/14)

Známa strana rádio

A = 2R × sen (π/n)

Áno n = 14:

A = 2R × Sen (π/14)

Známy obvod na strane

Obvod je súčet bokov. Keď je Tetradecágono pravidelný:

P = N⋅a = 14 šu

Ak je tetradecágono nepravidelný, všetky strany sa musia pridať priamo, aby sa získal obvod.

Známa oblasť na strane

A = ¼ na² × detská postieľka (π/n)

Pre n = 14:

A = ¼ (14²) × postieľka (π/14) = (7/2) a² × postieľka (π/14)

Známa oblasť

A = N⋅l_Do ² × TG (π/n)

Užívanie n = 14 výsledkov:

A = 14l_Do ² × TG (π/14)

Oblasť založená na obvode a apothéme

A = (p × l_Do)/2

Môže vám slúžiť: Bayesova veta

Miera vnútorného uhla

 Keď n = 14, vnútorný uhol meraní tetradekugono v stupňoch:

I = 12 × 180 ° /14 = 154.286 °

Meranie vonkajšieho uhla

E = 360 °/n

Kedy n = 14 máte:

E = 25.7143 °

Diagonála

Vzorec na výpočet počtu diagonálov prítomných v ľubovoľnom polygóne, pravidelnom alebo nie, je:

Pre n = 14:

D = 14 × 11/2 = 77 diagonálov

Príklady

Ďalší príklad Tetradecágonu

Pravidelné polygóny sa objavujú opakovane v mnohých vzoroch, ako sú meny. V prípade pravidelného tetradagónu sa to objavuje v malajzijských pamätných minciach, ktoré predstavujú jeho strany pre každú zo štrnástich konfederačných štátov tohto národa.

Konkávny a konvexný tetradecágonos

Všeobecne platí, že polygóny, ako je tetradekugono, môžu byť v prvom prípade konvexné alebo konkávne, miera ich vnútorných uhlov nepresahuje 180 °. Pravidelný tetradech je konvexný ako akýkoľvek pravidelný polygón, pretože ktorýkoľvek z jeho vnútorných uhlov meria 154.286 °.

Na druhej strane, v konkávnom tetradechu, jeden alebo viac jeho vnútorných uhlov meria viac ako 180 °.

Numerický príklad

Vzhľadom na pravidelný tetradagon, ktorého bočné meria 5 cm, nájdete:

a) obvod
b) meranie apotheme
c) Dĺžka rádiu
d) oblasť

Odpovedať

a) Pretože ide o pravidelný polygón, obvod je:

P = 14 × 5 cm = 70 cm.

b) z rovnice A = 2L_Do × Tg (π/14), kde a = 5 cm, apotHem l_Do:

L_Do = a / [2 × tg (π / 14)] = 5 cm / 0.4565 = 21.9064 cm

c) Rádio R sa dá vypočítať pomocou a = 2r × sen (π/14):

R = a / [2 × sin (π / 14)] = 5 cm / 0.4565 = 22.4698 cm

d) Existuje niekoľko alternatív pre oblasť, napríklad A = (p × l_Do)/2:

A = (70 × 21.9064)/2 cm² = 1533.45 cm².

Odkazy

1. Alexander, D. 2013. Geometria. 5. Vydanie. Učenie sa.
2. Geometria arturo. Všeobecná metóda kreslenia polygónov zaradených do obvodov. Obnovené z YouTube.com
3. Kalkulačka polievky. Pravidelná kalkulačka polygónu. Obnovené z: kalkulačky.com.
4. Kresba. Pravidelné polygóny. Obnovené z: kresby.com.
5. Requena, b. Konkávny polygón. Získané z: Universoformulas.com.
6. Wikipedia. Stavané polygón. Obnovené z: je.Wikipedia.orgán.