Najmenšie štvorce

Aká je metóda minimálnych štvorcov?

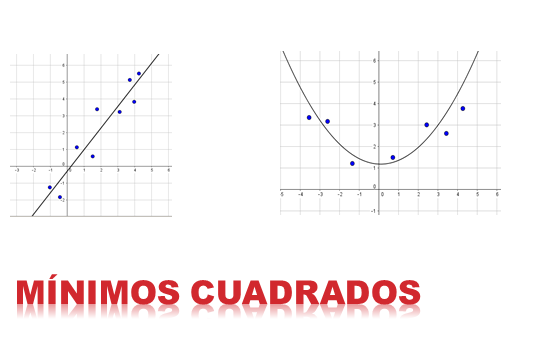
Spôsob Najmenšie štvorce Je to jedna z najdôležitejších aplikácií v prístupe k funkciám. Cieľom je nájsť krivku tak, že vzhľadom na súbor uprataných párov sa táto funkcia lepšie priblíži k údajom. Funkciou môže byť čiara, kvadratická krivka, kubická atď.

Myšlienka metódy je minimalizovať súčet štvorcov rozdielov v súradnici (komponent y), medzi bodmi vyvolanými zvolenou funkciou a bodmi patriacimi k súboru údajov.

Metóda minimálneho štvorca

Pred podaním metódy musíme najprv byť jasný v tom, čo „sa lepšie blíži“. Predpokladajme, že sa vyhľadá čiara y = b+mx, ktorá najlepšie predstavuje sadu n bodov, konkrétne (x1, y1), (x2, y2)…, (xn, yn).

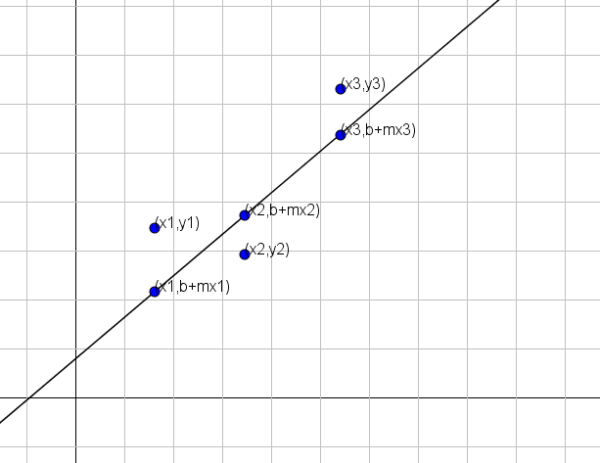
Ako je znázornené na predchádzajúcom obrázku, ak by premenné x a y súviseli s riadkom y = b+mx, potom pre x = x1 zodpovedajúca hodnota y by bola b+mx1. Táto hodnota sa však líši od skutočnej hodnoty y, ktorá je y = y1.

Pamätajte, že v rovine je vzdialenosť medzi dvoma bodmi daná nasledujúcim vzorcom:

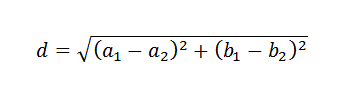
S ohľadom na to, aby ste zistili, ako zvoliť riadok y = b+mx, ktorý sa najlepšie blíži k daným údajom a čiara.

Pretože vzdialenosť medzi bodmi (x1, y1) a (x1, b+mx1) je y1- (b+mx1), náš problém sa mení na nájdenie čísel M a b tak, aby nasledujúci súčet je minimálny:

Môže vám slúžiť: zelená veta, demonštrácia, aplikácie a cvičenia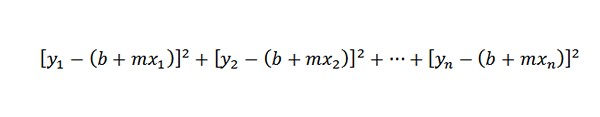

Čiara, ktorá spĺňa túto podmienku, je známa ako „prístup k línii minimálnych štvorcov k bodom (x1, y1), (x2, y2), ..., (xn, yn)“.

Po získaní problému zostáva iba zvoliť metódu na nájdenie prístupu minimálnymi štvorcami. Ak sú body (x1, y1), (x2, y2), ..., (xn, yn) všetky na riadku y = mx+b, museli by sme byť kolineal a:

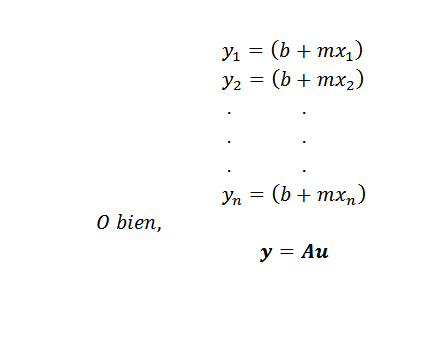
V tomto výraze:

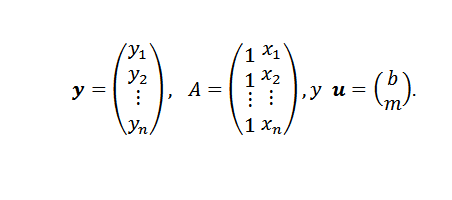
Nakoniec, ak body nie sú kolineálne, potom y-au = 0 a problém sa môže preložiť do nájdenia vektora alebo tak, aby euklidovský štandard je minimálny.

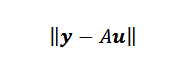
Nájdenie minimalizujúceho vektora alebo nie je také ťažké, ako by ste si mohli myslieť. Pretože a je matica nx2 a u je matica 2 × 1, máme, že vektor Au je vektor v rⁿ a patrí k obrazu A, ktorý je podprostorom Rⁿ S rozmerom nie viac ako dvaja.

Budeme predpokladať, že n = 3 ukážeme, aký je postup, ktorý sa musí dodržiavať. Ak n = 3, obraz A bude rovina alebo čiara, ktorá prechádza pôvodom.

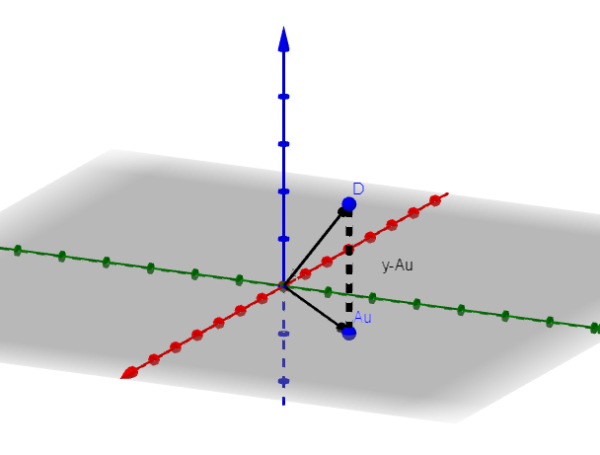
Nech V minimalizačný vektor. Na obrázku si uvedomujeme, že Y-Au je minimalizovaný, keď je ortogonálny pre obraz a. To znamená, že ak V je minimalizujúci vektor, potom sa stáva, že:

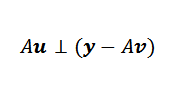
Potom môžeme vyššie uvedené vyjadriť týmto spôsobom:

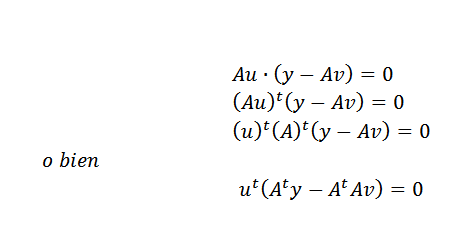
Môže sa to stať iba vtedy, ak:

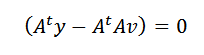
Nakoniec, zúčtovanie v, musíme:

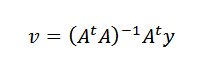
Odvtedy je to možné urobiť^tónA je invertibilné vždy, keď n body, pretože údaje nie sú kolineal.

Teraz, ak namiesto toho, aby sme hľadali čiaru, chceme nájsť podobenstvo (ktorého výraz by mal formu Y = a+bx+cx²), Že to bola lepšia aproximácia v údajových bodoch, postup by bol opísaný nižšie.

Môže vám slúžiť: celé čísla

Keby boli dátové body v tomto podobenstve, muselo by to:

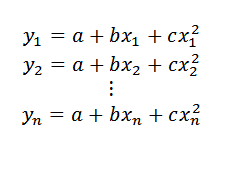
Potom:

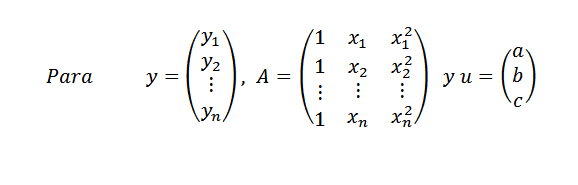
Podobne dokážeme písať y = au. Ak všetky body nie sú v podobenstve, máme, že Y-Au sa líši od nuly pre akýkoľvek vektor u a náš problém je opäť: nájdite vektor u v R3 tak, aby jeho norma || y-au || byť čo najviac.

Opakovaním predchádzajúceho postupu sa môžeme dostať k vektorovi, ktorý je:

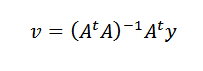
Vyriešené cvičenia

Cvičenie 1

Nájdite čiaru, ktorá najlepšie vyhovuje bodom (1.4), (-2,5), (3, -1) a (4.1).

Riešenie

Musíme:

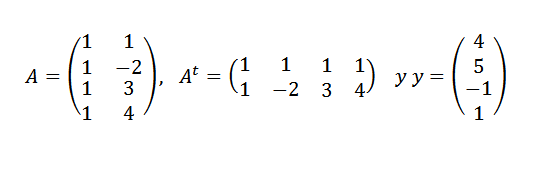
Potom:

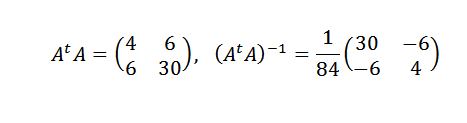
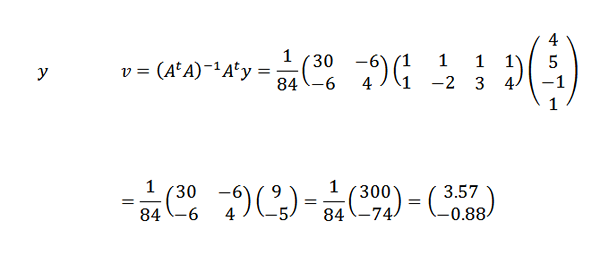
Preto sme dospeli k záveru, že čiara, ktorá najlepšie vyhovuje bodom, je daná:

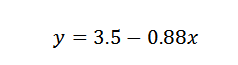
Cvičenie 2

Predpokladajme, že objekt je spadnutý z výšky 200 m. Pri páde sa prijmú tieto opatrenia:

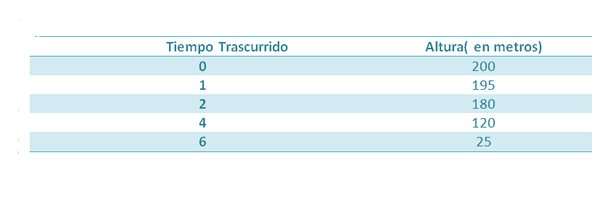
Vieme, že výška tohto objektu po uplynutí času je daná:

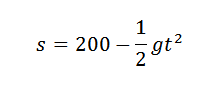
Ak chceme získať hodnotu G, môžeme hľadať podobenstvo, ktoré je lepším prístupom k piatim bodom uvedeným v tabuľke, a preto by sme mali, že koeficient, ktorý sprevádza T² Bude to rozumný prístup k (-1/2) g, ak sú merania presné.

Musíme:

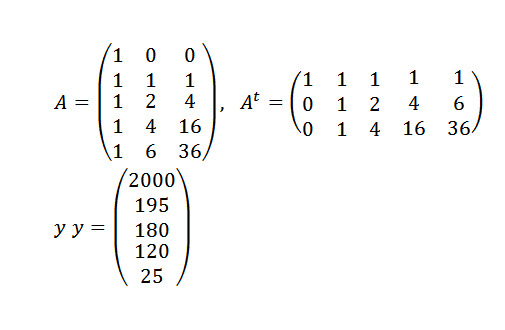
A potom:

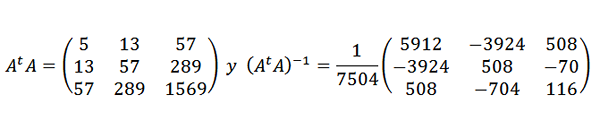
Dátové body sú teda upravené nasledujúcim kvadratickým výrazom:

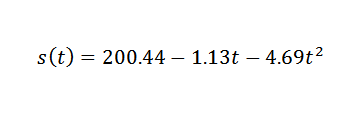
Takže musíte:

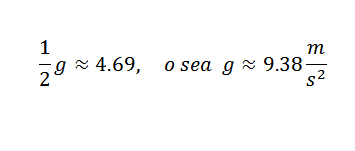
Toto je hodnota, ktorá je primerane blízko správnej, ktorá je g = 9,81 m/s². Aby sa získala presnejšia g G, bolo by potrebné začať od presnejších pozorovaní.

Aká je minimálna štvorcová metóda pre?

V problémoch, ktoré sa vyskytujú v prírodných alebo spoločenských vedách.

Môže vám slúžiť: Proporcionálna variácia

Napríklad v ekonómii sa môžeme vzťahovať na náklady (C), príjmy (i) a zisky (u) prostredníctvom jednoduchého vzorca:

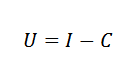
Vo fyzike môžeme súvisieť s zrýchlením spôsobeným gravitáciou, časom, v ktorom pokles objektu a výška objektu podľa zákona:

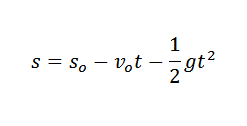
V predchádzajúcom výraze s_ani Je to počiatočná výška uvedeného objektu a V_ani Je vaša počiatočná rýchlosť.

Nájdenie vzorcov, ako sú tieto, však nie je jednoduchá úloha; Zvyčajne zodpovedá odborníkovi v službe pracovať s mnohými údajmi a opakovane vykonáva niekoľko experimentov (s cieľom overiť, či sú získané výsledky konštantné), aby sa našli vzťahy medzi rôznymi údajmi.

Bežným spôsobom, ako to dosiahnuť.

Jedným zo spôsobov, ako nájsť funkciu, ktorá „lepšie sa blíži“, uvedené údaje sú metódou štvorcových minimá.

Okrem toho, ako sme tiež videli v cvičení, vďaka tejto metóde môžeme dosiahnuť pomerne blízke prístupy k fyzickým konštántam.