Charakteristiky kolmej línie, príklady, cvičenia

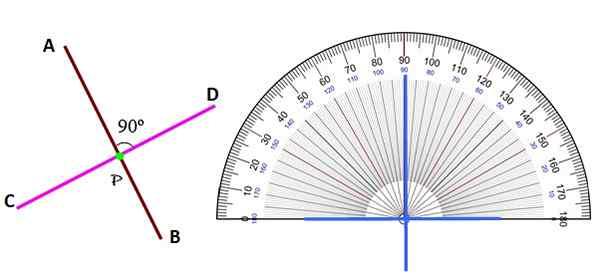
A kolmo Je to taký, ktorý tvorí uhol 90 ° vzhľadom na inú čiaru, krivku alebo povrch. Všimnite si, že keď sú dve čiary kolmé a na rovnakej rovine, keď sú rezané, tvoria štyri rovnaké uhly, každý z 90 °.

Ak jeden z uhlov nie je 90 °, hovorí sa, že čiary sú šikmé. Kolmé čiary sú časté v dizajne, architektúre a konštrukcii, napríklad v sieti potrubia nasledujúceho obrázka.

postava 1. Rovná potrubia a početné kolmé čiary. Koľko uhlov 90 ° sa dá počítať na tomto obrázku? Zdroj: piqsels.

Orientácia kolmých čiar môže byť rozmanitá, napríklad tie, ktoré sú uvedené nižšie:

Obrázok 2. Kolmé čiary v rovine. Zdroj: f. Zapata.

Bez ohľadu na polohu sa kolmé čiary rozpoznávajú identifikáciou uhla medzi nimi ako 90 °, pomocou dopravníka.

Všimnite si, že na rozdiel od rovnobežných čiar v rovine, ktoré sa nikdy nepretínajú, kolmé to vždy robia v bode P, nazývané noha jedného z riadkov na druhej. Preto sú tiež dve kolmé čiary Sekundárstvo.

Akákoľvek čiara má na ňu nekonečnú kolmo, pretože tým, že vytlačením segmentu AB doľava alebo doprava v segmente CD budeme mať nový kolmý s inou nohou.

V kolomok, ktorý prechádza práve v strede segmentu, sa nazýva bisektor uvedeného segmentu.

[TOC]

Príklady kolmých línií

V mestskej krajine sú často kolmé línie. Na nasledujúcom obrázku (obrázok 3) iba niekoľko z mnohých kolmých čiar, ktoré sa oceňujú na jednoduchej fasáde tejto budovy a jej prvkov, ako sú dvere, potrubia, kroky a ďalšie: viac: viac:

Môže vám slúžiť: Fourier Discreet Transformed: Vlastnosti, aplikácie, príklady Obrázok 3. Na fasáde spoločnej budovy, ako je táto, je veľa kolmých línií. Zdroj: Richard Kang cez Flickr.

Dobrá vec je, že tri riadky kolmé na seba, nám pomáhajú stanoviť umiestnenie bodov a objektov vo vesmíre. Sú súradnicové osi identifikované ako X os x, Os y a Z, Jasne viditeľné v rohu obdĺžnikovej miestnosti ako nasledujúce:

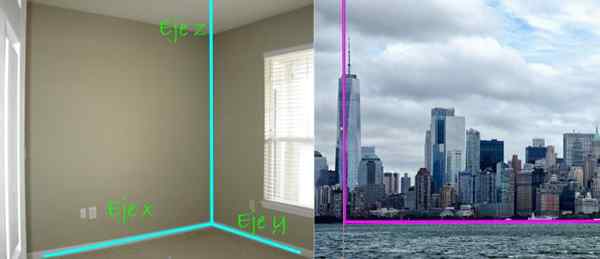Obrázok 4. Systém karteziánskej osi pozostáva z troch riadkov kolmo na seba, každý má preferenčný smer vo vesmíre. Kredity vľavo: Treybunn 2 cez Flickr. Pravý obraz; Nepotrel.

V panoramatickom výhľade na mesto je napravo varovaná kolmo medzi mrakodrapmi a pôdou. Prvý by povedal, že sa nachádza v celom Z, Zatiaľ čo pôda je lietadlom, čo je v tomto prípade lietadlo Xy.

Ak pôda predstavuje lietadlo Xy, Mrakodrap je tiež kolmý na akúkoľvek cestu alebo ulicu, ktorá zaručuje jeho stabilitu, pretože naklonená štruktúra je nestabilná.

A na uliciach, kdekoľvek obdĺžnikové rohy, existujú kolmo. Mnoho ciest a ulíc má kolmé usporiadanie za predpokladu, že pôda a geografické nehody to umožňujú.

Aby sa náhle vyjadrila kolmo medzi čiarami, segmentmi alebo vektormi, používa sa symbol ⊥. Napríklad, ak riadok L₁ je kolmo na čiaru L₂, napísali sme:

L₁ ⊥ l₂

Viac príkladov kolmých čiar

- V dizajne sú kolmé čiary veľmi prítomné, pretože mnoho bežných objektov je založených na štvorci a obdĺžnikoch. Tieto kvadrilaterály sa vyznačujú vnútornými uhlami 90 °, pretože ich strany sú dve až dve paralelné:

Môže vám slúžiť: Všeobecná parabola rovnica (príklady a cvičenia)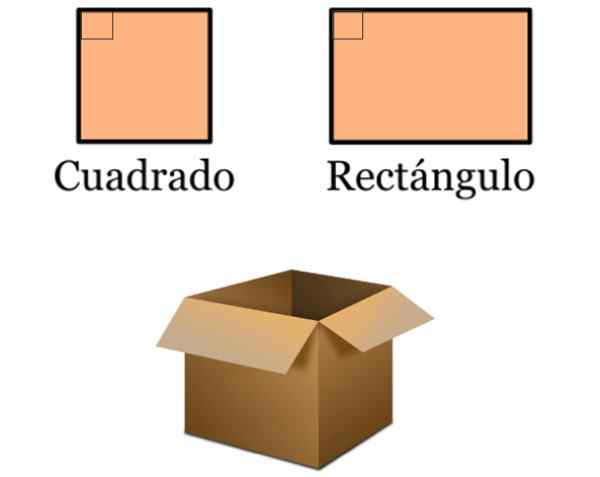 Obrázok 5. Štvorce a obdĺžniky sú súčasťou mnohých vzorov, ako napríklad v tejto jednoduchej kartónovej skrinke na ukladanie tovaru. Zdroj: f. Zapata.

- Súdy, na ktorých sa praktizujú rôzne športy, sú vymedzené mnohými štvorcami a obdĺžnikmi. Tieto zase obsahujú kolmé čiary.

- Dva zo segmentov, ktoré tvoria obdĺžnikový trojuholník, sú navzájom kolmé. Nazývajú sa Kategórie, zatiaľ čo zostávajúca čiara sa volá preprava.

- Vektorové vedenia elektrického poľa sú kolmé na povrch elektrostatickej rovnováhy.

- Pre naloženého vodiča sú vybavenie a vybavenie vždy kolmé na zariadenia elektrického poľa.

- V potrubných systémoch alebo potrubiach používaných na prepravu rôznych druhov tekutín, ako je napríklad plyn, ktoré sú na obrázku 1, je bežné pre lakte v pravom uhle. Preto tvoria kolmé línie, ako je prípad kotlovej miestnosti:

Obrázok 6. Potrubia v kotlovej miestnosti. Zdroj: Wikimedia Commons. Roger McLassus/CC By-S (http: // creativeCommons.Org/licencie/By-SA/3.0/)

Cvičenia

- Cvičenie 1

Nakreslite dve kolmé čiary podľa pravidla a kompasu.

Riešenie

Je to veľmi jednoduché, podľa týchto krokov:

-Prvý riadok je nakreslený, nazývaný AB (čierna).

-Nad (alebo nižšie, ak sú preferované) AB Marks Point P, kde kolmý prejde. Ak je p tesne nad (alebo nižšou) polovicou AB, povedal kolmo.

-S kompasom sústredeným na P je nakreslený kruh, ktorý znižuje AB v dvoch bodoch, zavolaný na „a b“ (červená).

Môže vám slúžiť: priateľské alebo priateľské čísla: príklady a ako ich nájsť

-Kompas v A'P je otvorený, zameriava sa na A 'a kruh je nakreslený, ktorý prechádza cez P (zelená).

-Zopakujte predchádzajúci krok, ale teraz otvára kompas dĺžku segmentu B'P (zelená). Oba oblúky obvodu sú rezané v bode Q pod p a samozrejme v druhom.

-Body p a q sú spojené s pravidlom a kolmo (modrá) je už pripravená.

-Nakoniec, všetky pomocné konštrukcie musia byť starostlivo vymazané a zostávajú iba kolmo.

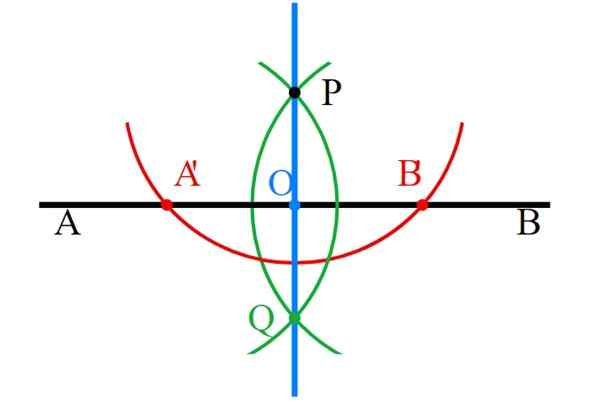Obrázok 6. Percendulárne čiary s pravidlom a Compas. Zdroj: Wikimedia Commons.

- Cvičenie 2

Dva riadky L₁ a l₂ Sú kolmé, ak ich príslušné svahy m₁ a m₂ Spĺňajú tento vzťah:

m₁ = -1/m₂

Vzhľadom na riadok y = 5x - 2 nájdite čiaru kolmo na ňu a prejdite bodom (-1, 3).

Riešenie

-Po prvé je sklon kolmej línie m_⊥, Ako je uvedené vo vyhlásení. Sklon pôvodnej čiary je M = 5, koeficient, ktorý sprevádza „X“. Tak:

m_⊥= -1/5

-Potom je postavená rovnica kolmej čiary a_⊥, výmena predtým nájdenej hodnoty:

a_⊥= -1/5x + b

-Potom sa stanoví hodnota B pomocou bodu daného vyhlásením (-1,3), pretože cez ňu musí prejsť kolmo:

y = 3

x = -1

Výmena:

3 = -1/5 (-1) + b

Hodnota B sa vymaže:

B = 3- (1/5) = 14/5

-Nakoniec je vytvorená konečná rovnica:

a_⊥= -1/5x + 14/5

Odkazy

1. Baldor, a. 2004. Geometria plochej a vesmíru. Kultúrne publikácie.
2. Clemens, s. 2001. Geometria s aplikáciami a riešením problémov. Addison Wesley.
3. Matematika je zábava. Kolmo. Získané z: Mathisfun.com.
4. Inštitút Monterey. Kolmo. Získané z: Montereyinstitute.orgán.
5. Wikipedia. Kolmo. Obnovené z: je.Wikipedia.orgán.