Trigonometrické limity, ako ich vyriešiť, vyriešené cvičenia

Ten trigonometrické limity Sú to obmedzenia funkcií tak, že tieto funkcie sú tvorené trigonometrickými funkciami.

Existujú dve definície, o ktorých je známe, že chápu, ako sa vykonáva výpočet trigonometrického limitu. Tieto definície sú:

- Limit funkcie „F“, keď „x“ má tendenciu „B“: spočíva v výpočte hodnoty, pri ktorej sa F (x) blíži ako „x“ blíži sa „b“, bez toho, aby uplatnil „b“.

- Trigonometrické funkcie: Trigonometrické funkcie sú sínusové, kosínové a tangenciálne funkcie označené sin (x), cos (x) a tan (x).

Ostatné trigonometrické funkcie sa získavajú z troch vyššie uvedených funkcií.

Limity funkcií

Aby sme objasnili koncept funkčného limitu, pokračujeme v zobrazení niekoľkých príkladov s jednoduchými funkciami.

- Limit f (x) = 3, keď „x“ má tendenciu „8“, sa rovná „3“, pretože funkcia je vždy konštantná. Nezáleží na tom, koľko „x“ stojí za to, hodnota f (x) bude vždy „3“.

- Limit f (x) = x-2, keď „x“ má tendenciu „6“, je „4“. Keď je "X" blízko „6“, potom „x-2“ sa blíži “6-2 = 4“.

- Limit g (x) = x², keď „x“ má tendenciu „3“, sa rovná 9, pretože keď sa „x“ blíži „3“, potom sa blíži „x²“ „3² = 9“.

Ako je možné poznamenať v predchádzajúcich príkladoch, výpočet limitu spočíva v hodnotení hodnoty, ktorej „x“ má tendenciu vo funkcii, a výsledkom bude hodnota limitu, hoci to platí iba pre kontinuálne funkcie.

Existujú komplikovanejšie limity?

Odpoveď je áno. Predchádzajúce príklady sú najjednoduchšie príklady limitov. Vo výpočtových knihách sú hlavné limitné cvičenia, ktoré generujú neurčitosť typu 0/0, ∞/∞, ∞ -∞, 0*∞, (1)^∞, (0)^0 a (∞)^0.

Môže vám slúžiť: Pythagorovské identity: demonštrácia, príklad, cvičenia

Tieto výrazy sa nazývajú neurčité, pretože sú to výrazy, ktoré matematicky dávajú zmysel.

Okrem toho, v závislosti od funkcií zapojených do pôvodného limitu, výsledok získaný pri riešení neurčení sa môže v každom prípade líšiť.

Príklady jednoduchých trigonometrických limitov

Na vyriešenie limitov je vždy veľmi užitočné poznať grafy zúčastnených funkcií. Nižšie sú uvedené grafy sínusových, kosínových a tangensových funkcií.

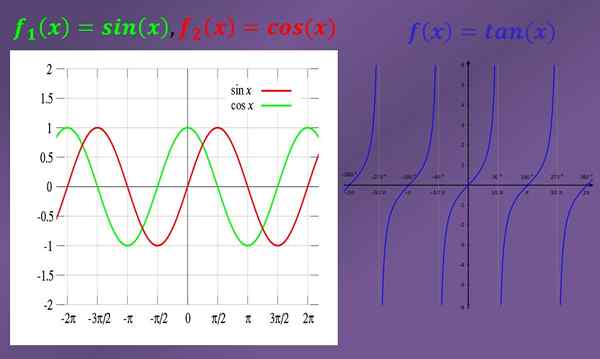
Niektoré príklady jednoduchých trigonometrických limitov sú:

- Vypočítajte limit bez (x), keď „x“ má tendenciu „0“.

Vidíte graf, vidíte, že ak sa „x“ blíži k „0“ (vľavo aj vpravo), potom sa grafika prsníka blíži „0“. Preto limit hriechu (x), keď „x“ má tendenciu „0“, je „0“.

- Vypočítajte hranicu cos (x), keď „x“ má tendenciu „0“.

Pozorovanie grafu kosínu je vidieť, že keď je „x“ blízko „0“, potom je graf kosínu blízko „1“. To znamená, že hranica cos (x), keď „x“ má tendenciu „0“, sa rovná „1“.

Limit môže existovať (byť číslom), ako je to v predchádzajúcich príkladoch, ale môže sa tiež stať, že neexistuje, ako je uvedené v nasledujúcom príklade.

- Limit opálenia (x), keď „x“ má tendenciu „π/2“ vľavo, sa rovná „+∞“, ako je vidieť v grafike. Na druhej strane, limit opálenia (x), keď „x“ má tendenciu „-π/2“ vpravo, sa rovná „-∞“.

Trigonometrické obmedzenia identity

Dve veľmi užitočné identity, keď sa vypočítajú trigonometrické limity, sú:

Môže vám slúžiť: nelineárne programovanie: metódy a cvičenia

- Limit „sin (x)/x“, keď „x“ má tendenciu „0“, sa rovná „1“.

- Limit „(1-COS (x))/x“, keď „x“ má tendenciu „0“, sa rovná „0“.

Tieto identity sa používajú veľmi často, keď máte nejakú neurčitosť.

Vyriešené cvičenia

Vyriešte nasledujúce limity pomocou vyššie opísaných identity.

- Cvičenie 1

Vypočítajte limit „f (x) = bez (3x)/x“, keď „x“ má tendenciu „0“.

Ak sa funkcia „F“ vyhodnotí v „0“, získanie neurčitosti typu 0/0. Preto sa musíme pokúsiť vyriešiť túto neurčitosť pomocou opísanej identity.

Jediným rozdielom medzi týmto limitom a identitou je číslo 3, ktoré sa objaví vo funkcii sínusu. Aby sa uplatňovala identita, musí sa funkcia „f (x)“ prepísať nasledovne „3*(bez (3x)/3x)“. Teraz sú argument prsníka aj menovateľ rovnaký.

Takže keď „x“ má tendenciu „0“, použitie identity je „3*1 = 3“. Preto limit f (x), keď „x“ má tendenciu „0“, sa rovná „3“.

- Cvičenie 2

Vypočítajte limit „g (x) = 1/x - cos (x)/x“, keď „x“ má tendenciu „0“.

Keď sa „x = 0“ nahradí v g (x) neurčitosť typu ∞ -∞. Na jeho vyriešenie sa frakcie odpočítajú, čo dáva výsledkom „(1-COS (x))/x“.

Teraz použitím druhej trigonometrickej identity je limit G (x), že „x“ má tendenciu „0“ rovnať 0.

- Cvičenie 3

Vypočítajte limit „h (x) = 4tan (5x)/5x“, keď „x“ má tendenciu „0“.

Opäť, ak sa H (x) vyhodnotí v „0“, získa sa neurčitosť typu 0/0.

Prepisovanie ako (5x) ako bez (5x)/cos (5x) Ukazuje sa, že h (x) = (bez (5x)/5x)*(4/cos (x))).

Môže vám slúžiť: vpísaný uhol kruhu: definícia, vety, príklady

Použitím tohto limitu 4/cos (x), keď „x“ má tendenciu „0“, sa rovná „4/1 = 4“ a prvá trigonometrická identita sa získa, že limit H (x), keď „x“ má tendenciu "0" sa rovná "1*4 = 4".

Pozorovanie

Trigonometrické limity nie je vždy ľahké vyriešiť. V tomto článku boli uvedené iba základné príklady.

Odkazy

1. Fleming, w., & Varberg, D. A. (1989). Matematika. Prentice Hall PTR.
2. Fleming, w., & Varberg, D. A. (1989). Matematika precalculus: prístup riešenia problémov (2, ilustrované ed.). Michigan: Prentice Hall.
3. Fleming, w., & Varberg, D. (1991). Algebra a trigonometria s analytickou geometriou. Pearson Vzdelanie.
4. Larson, R. (2010). Predbežný (8 ed.). Učenie sa.
5. Lojálny, j. M., & Viloria, n. G. (2005). Plochá analytická geometria. Mérida - Venezuela: Venezuelský redaktor C. Do.
6. Pérez, C. D. (2006). Predkválka. Pearson Vzdelanie.
7. Purcell, e. J., Varberg, D., & Rigdon, s. A. (2007). Kalkulácia (Deviate vydanie.). Sála.
8. Saenz, J. (2005). Diferenciálny výpočet s včasnými transcendentnými funkciami pre vedu a inžinierstvo (Druhé vydanie ed.). Preprava.
9. Scott, C. Do. (2009). Geometria karteziánskej roviny, časť: Analytical Conics (1907) (Opakovanie Ed.). Bleskový zdroj.
10. Sullivan, m. (1997). Predkválka. Pearson Vzdelanie.